水管冷却是大体积混凝土温度控制的重要措施[1-3]。由于水管冷却时产生的温度场十分复杂,它实际上是一把双刃剑,既可有效降低混凝土温度,但若降温速率过快,又会引起混凝土严重开裂。针对这个问题,朱伯芳[4]提出了“小温差、早冷却、缓慢冷却”的通水冷却原则。目前,该通水冷却原则在高混凝土坝工程中得到广泛应用。例如,针对溪洛渡特高拱坝,设计单位根据拱坝混凝土温度防裂特点,将水管冷却分为3期(1期、中期和2期)9个阶段[5],并设计给出了分期冷却温度过程线(简称:设计温控过程线),每个阶段严格控制目标温度和温度变化速率等,施工单位按设计温控过程线进行通水冷却,获得了良好的温控防裂效果。由于混凝土浇筑仓尺寸较大,一般厚1~3 m,横河向宽20 m左右,顺河向长20~60 m不等。实际施工时,每个混凝土浇筑仓至多埋设1~2支温度计。在温控实践过程中发现,由于混凝土浇筑仓在通水冷却期间的温度场十分复杂,而封拱温度一般是指混凝土浇筑仓平均温度,如何对混凝土浇筑仓平均温度进行实时监测是一个重要问题。
分析设计温控过程线可知,混凝土最高温度、冷却目标温度、封拱温度和降温速率等,均是针对混凝土浇筑仓平均温度而言,即设计温控过程线是混凝土浇筑仓的平均温度历程。显然,在混凝土浇筑仓中如何埋设温度计,使实测温度能够表征混凝土浇筑仓的平均温度为工程建设单位所关注,但该问题尚未见有关文献报导。本文拟采用优化算法和水管冷却有限元法相结合,探讨含冷却水管混凝土坝中温度计位置的分布规律。
1 温度计埋设位置优选原理 1.1 水管冷却有限单元法计算原理水管冷却效果的模拟是含冷却水管大体积混凝土温度场仿真分析的一个难点。目前,分析混凝土坝水管冷却效果主要有两种计算模型:水管冷却有限元法和水管冷却等效热传导法。水管冷却有限元法是在水管附近布置密集的有限元网格,以反映水管附近很大的温度梯度,采用迭代法计算水管水温与混凝土进行热交换而导致沿程水温逐渐增大,从而获得温度场;而水管冷却等效热传导法则把冷却水管看成热汇,在平均意义上考虑水管冷却的效果,不需要在水管附近布置密集的有限元网格,采用通常的网格即可获得温度场。水管冷却有限元法的计算原理和水管冷却等效热传导法计算原理在文献[1, 6-8]中有详细叙述,不再赘述。为了获得精度良好的含冷却水管混凝土浇筑仓的温度分布,采用水管冷却有限元法仿真计算的温度场更符合实际情况[9-10],为此,采用Visual Fortran编制的水管冷却有限元法仿真分析程序[7]。
1.2 基于优化算法优选温度计埋设位置由于设计温控过程线是混凝土浇筑仓的平均温度历程,换句话说,首先需要获得含冷却水管的混凝土浇筑仓的平均温度历程,然后在该混凝土浇筑仓空间中寻找温度历程与浇筑仓平均温度历程最接近的几何坐标位置(x*, y*, z*)。如果在该几何坐标位置(x*, y*, z*)处埋设温度计,那么实测温度即可反映混凝土浇筑仓的平均温度状态。即温度计埋设位置是一个几何坐标位置不确定性问题,可以采用优化算法来求解。本文选取优化算法进行温度计几何位置优选的求解。
(1) 混凝土浇筑仓平均温度。设t时刻,混凝土浇筑仓在通水冷却时的平均温度Ta(t)为
| ${T_{\rm{a}}}\left( t \right) = \sum\limits_{\rm{e}} {} \left( {\sum\limits_{\rm{g}} {} {T_{\rm{g}}}\left( t \right){\rm{ }}{V_{\rm{g}}}} \right)/\sum\limits_{\rm{e}} {} \left( {\sum\limits_{\rm{g}} {} {V_{\rm{g}}}} \right)$ | (1) |
式中:Tg(t)是t时刻单元高斯点温度(℃);Vg为单元高斯点占有体积,可采用该高斯点的雅可比行列式|J|计算得到(m3);
(2) 混凝土浇筑仓内任意点温度。混凝土浇筑仓内任意点的温度为
| $T{\rm{ }}\left( {x,{\rm{ }}y,{\rm{ }}z,{\rm{ }}t} \right) = \sum\limits_i {} {N_i}\left( {x,{\rm{ }}y,{\rm{ }}z} \right){\rm{ }}{T_i}\left( t \right)$ | (2) |
式中:Ni(x, y, z)为形函数; Ti(t)为t时刻节点的温度(℃)。
(3) 温度计几何位置优选数学模型。由混凝土浇筑仓平均温度和混凝土浇筑仓内任意点温度,获得温度计几何位置优选的数学形式可以描述如下:
求X=[x y z], 使
| $\begin{array}{l} Z = f{\rm{ }}\left( X \right) = \sum\limits_{j = 1}^N {} {({T_{\rm{a}}}({t_j}) - T{\rm{ }}(x,{\rm{ }}y,{\rm{ }}z,{\rm{ }}{t_j}))^2}/N = \\ (\sum\limits_{j = 1}^N {} {({T_{\rm{a}}}({t_j}) - \sum\limits_i {} {N_i}\left( {x,{\rm{ }}y,{\rm{ }}z} \right){\rm{ }}{T_i}({t_j}))^2}/N) \to {\rm{min}} \end{array}$ | (3) |
满足约束条件:x≤x≤x, y≤y≤y, z≤z≤z
式中:x,x,y,y,z,z分别为坐标x,y和z的上下限(m)。
实际上,式(3) 是在混凝土浇筑仓内寻找与混凝土浇筑仓平均温度过程线差值最小的温度计的位置。
(4) 温度计几何位置优选求解步骤。
步骤1:混凝土浇筑仓中冷却水管一般蛇形布置(见图 1),沿流水方向的AB和CD面为近似对称面,可以认为该对称面为绝热边界面,建立含冷却水管的混凝土模型如图 2。对该混凝土模型采用水管冷却有限元法进行温度场仿真计算,获得含冷却水管的混凝土模型温度场,同时,按式(1) 计算含冷却水管的混凝土模型的平均温度历程。

|
图 1 蛇形水管模型 Figure 1 Serpentine tube model |

|
图 2 水管简化模型 Figure 2 Simplified model of water pipe |
步骤2:选取含冷却水管混凝土模型的典型截面(一般取混凝土棱柱体中间截面),由截面单元的节点温度,采用形函数获得截面任意点温度。
步骤3:由步骤1计算的平均温度历程和步骤2计算的任意点温度,建立温度计几何位置优选模型。
步骤4:采用优化算法求解温度计几何位置优选模型,获得温度计埋设最优的几何位置。
2 算例分析据已有工程经验[1],混凝土坝中埋设的水管间距通常为1.0~3.0 m。混凝土绝热温升表达式为θ(t)=25.3(1-exp(-0.315τ)),混凝土导热系数λ=8.49 kJ/(m·h· ℃),比热c=0.995 kJ/(kg· ℃),密度ρ=2 400 kg/m3;通水流量qw=24 m3/d,比热cw=4.187 kJ/kg· ℃,密度ρw=1 000 kg/m3。
2.1 含冷却水管混凝土模型的建立及仿真计算将冷却水管蛇形布置的混凝土浇筑仓简化为含冷却水管的混凝土棱柱体。设其棱柱体长L=100 m,设计了4种不同棱柱体截面尺寸,宽×高分别为1.0 m×1.0 m,1.5 m×1.5 m,1.0 m×1.5 m,2.0 m×1.5 m,在混凝土棱柱体横截面的正中心方向布置了1根外径为φ=32 mm的冷却水管,即冷却水管水平间距分别为1.0, 1.5和2.0 m,垂直间距分别为1.0和1.5 m。
假设混凝土棱柱体四面均为绝热边界,混凝土的初始温度取10 ℃,冷却水入口温度为10 ℃。采用水管冷却有限元法进行通水冷却期间的温度场仿真计算,通水开始时间为1 d,连续通水10 d。按式(1) 计算的混凝土棱柱体平均温度过程线如图 3。

|
图 3 不同水管间距下混凝土棱柱体平均温度过程线 Figure 3 Average temperature process line of concrete prism with different water pipe spacings |
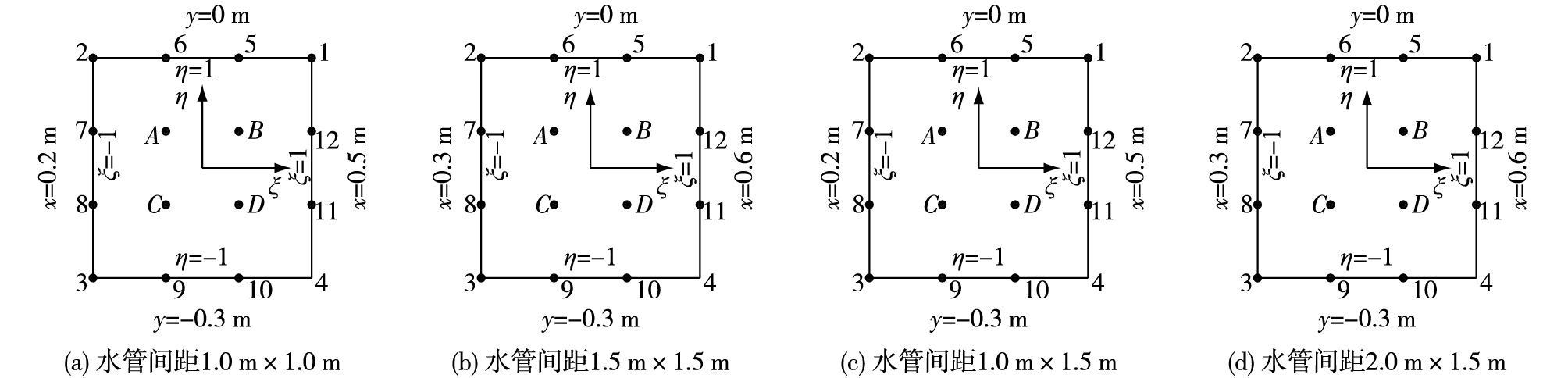
选取混凝土棱柱体中间50 m所在截面进行分析。由于棱柱体6个表面绝热,截面温度场呈对称分布,为此,对1/4截面的温度场进行分析。在进行水管冷却有限元计算时,混凝土棱柱体采用6面体8节点单元,中间截面为四边形4节点单元,由式(2) 计算截面任意点的温度不方便。为便于由节点温度获得截面内任意点的温度,引入四边形12节点单元,通过采用四边形12节点等参单元替代四边形4节点等参单元来简化截面内任意点温度的计算。如图 4所示,依据温度场仿真计算结果,给出了四边形12节点单元的上下限,该四边形12节点单元区域包含9个四边形4节点单元。
|
图 4 四边形12节点单元 Figure 4 A quadrilateral with 12-node element |
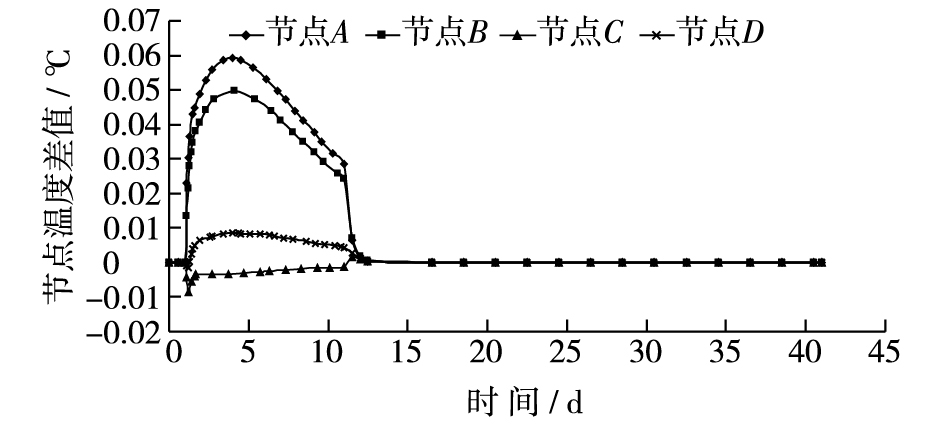
以图 4(a)为例,采用四边形12节点等参单元形函数[11]计算四边形单元中A, B, C和D共4个点的温度历程,并与温度场仿真计算的节点温度历程进行对比分析,见图 5。
由图 5可见,宽×高为1.0 m×1.0 m截面单元中A, B, C和D点的温度差值分布在[-0.01, 0.06]范围内,计算误差在0.03%以内,因此,通过采用四边形12节点等参单元代替四边形4节点等参单元来简化截面内任意点温度的计算是可行的。
|
图 5 四边形12节点插值温度和仿真计算节点温度差值 Figure 5 Difference comparison between quadrilateral 12-node interpolation temperature and simulated calculation node temperature |
引入四边形12节点等参单元获得的截面任意点温度为:
| $T{\rm{ }}\left( {\xi ,{\rm{ }}\eta ,{\rm{ }}t} \right) = \sum\limits_{i = 1}^{12} {} {N_i}\left( {\xi ,{\rm{ }}\eta } \right){\rm{ }}{T_i}\left( t \right)$ | (4) |
式中:Ti(t)为对应节点温度;Ni(ξ, η)为四边形12节点等参单元的形函数,计算式为
| $\left. \begin{array}{c} {N_i} = (1 + {\xi _i}\xi )(1 + {\eta _i}\eta )\left[ {9({\xi ^2} + {\eta ^2}) - 10} \right]/32\left( {i = 1,{\rm{ }}2,{\rm{ }}3,{\rm{ }}4} \right)\\ {\rm{ }}{N_i} = 9(1 + {\eta _i}\eta )(1 - {\xi ^2})(1 + 9{\xi _i}\xi )/32\left( {i = 5,{\rm{ }}6,{\rm{ }}9,{\rm{ }}10} \right)\\ {\rm{ }}{N_i} = 9(1 + {\xi _i}\xi )(1 - {\eta ^2})(1 + 9{\eta _i}\eta )/32\left( {i = 7,{\rm{ }}8,{\rm{ }}11,{\rm{ }}12} \right) \end{array} \right\}$ | (5) |
温度计位置优选分析表明,在截面上存在多个位置的温度历程和浇筑仓平均温度历程接近。为此,采用固定η,即分别取η=-1.0,-0.9,…, -0.1,0,0.1,…,0.9,1.0,然后采用一维优化搜索法对ξ进行优选。此时,在ξ-η局部坐标系下温度计几何位置优选的数学形式为求ξ, 使
| $Z = f{\rm{ }}\left( \xi \right) = \sum\limits_{j = 1}^N {} \left( {{T_{\rm{a}}}({t_j}) - \sum\limits_i {} {N_i}\left( {\xi ,{\rm{ }}\eta } \right){\rm{ }}{T_i}({t_j})} \right) \to {\rm{min}}$ | (6) |
满足约束条件:-1≤ξ≤1
式中:N由温度场仿真计算的时间步来确定,在仿真分析时,前11 d的时间步为0.1 d,11~41 d的时间步为0.5 d,因此,取N=170。
由于在固定η时,不一定存在对应的ξ来保证f (ξ)→min,因此,分析采用了最小误差和最大优选次数的双重优选控制标准。
2.4 温度计位置优选模型求解采用一维优化搜索法对式(6) 进行优选求解,获得温度计位置ξ-η值,然后采用下式获得x-y坐标值:
| $x = \sum\limits_{i = 1}^{12} {} {N_i}\left( {\xi ,{\rm{ }}\eta } \right){\rm{ }}{x_i},y = \sum\limits_{i = 1}^{12} {} {N_i}\left( {\xi ,{\rm{ }}\eta } \right){\rm{ }}{y_i}$ | (7) |
式中: xi和yi分别为节点i的坐标。
由于所选计算模型边界为绝热边界,可由对称性得到4种典型水管间距优选的温度计位置,计算结果如图 6所示。

|
图 6 不同水管间距下温度计优选位置分布 Figure 6 Optimum position distribution of thermometers under different water pipe spacings |
计算结果分析如下:① 1.0 m×1.0 m,1.5 m×1.5 m和2.0 m×1.5 m这3个截面温度计优选位置均呈抛物线分布,分布位置分别距离水管中心约0.20~0.35 m,0.35~0.50 m和0.45~0.55 m处;1.0 m×1.5 m截面温度计优选位置分布近似为线性,分布位置距离水管中心约0.25~0.50 m处。② 对比1.0 m×1.0 m与1.5 m×1.5 m截面,截面尺寸增大50%,温度计分布范围靠近截面边缘处,而温度计优选位置分布呈抛物线分布规律不变,但抛物线曲率变大。③ 对比1.0 m×1.5 m, 1.5 m×1.5 m与2.0 m×1.5 m截面,随着截面宽度的缩小,截面宽高比增大,温度计埋设优选位置分布范围变大,当截面宽度为1.0 m时,温度计的优选位置分布由抛物线分布变为近似直线分布。
3 结语针对埋设在混凝土浇筑仓中温度计位置不确定问题,建立温度计位置优选模型,通过一维优化搜索法求解最优的温度计位置,并探讨含冷却水管混凝土中温度计位置的分布规律,得到如下结论:
(1) 在获取截面内任意点温度时,引入四边形12节点单元,计算讨论了采用四边形12节点等参单元替代四边形4节点等参单元来简化计算截面内任意点温度的可行性,结果表明简化计算可行。
(2) 通过对不同截面温度计优选位置计算结果分析可知,1.0 m×1.5 m截面温度计优选位置分布近似为线性分布,其他截面温度计优选位置分布呈抛物线分布。随着截面宽度的缩小,温度计优选位置的分布范围增大,当截面宽度为1.0 m时,温度计的优选位置由抛物线分布变为近似直线分布。
(3) 针对不同的水管间距,按照优选位置埋设温度计,通过温度计获取的实测温度可表征混凝土浇筑仓的平均温度历程,指导混凝土坝的温度监控。由于实际混凝土工程的边界条件十分复杂,研究时计算模型采用绝热边界与实际情况存在一定差异,该问题有待进一步研究。
| [1] |
朱伯芳. 大体积混凝土温度应力与温度控制[M]. 北京: 中国电力出版社, 1999. ( ZHU Bofang. Thermal stresses and temperature control of mass concrete[M]. Beijing: China Electric Power Press, 1999. (in Chinese))
|
| [2] |
朱伯芳. 混凝土坝理论与技术新进展[M]. 北京: 中国水利水电出版社, 2009. ( ZHU Bofang. New developments in the theory and technology of concrete dams[M]. Beijing: China Water Power Press, 2009. (in Chinese))
|
| [3] |
黄耀英, 何光宇, 周宜红, 等. 水管冷却等效热传导方程中混凝土初温的研究[J]. 武汉大学学报(工学版), 2013, 46(1): 105-108. ( HUANG Yaoying, HE Guangyu, ZHOU Yihong, et al. Research of initial temperature in equivalent heat conduction equation of pipe cooling[J]. Engineering Journal of Wuhan University, 2013, 46(1): 105-108. (in Chinese)) |
| [4] |
朱伯芳. 小温差早冷却缓慢冷却是混凝土坝水管冷却的新方向[J]. 水利水电技术, 2009, 40(1): 44-50. ( ZHU Bofang. Pipe cooling of concrete dam from earlier age with smaller temperature difference and longer time[J]. Water Resources and Hydropower, 2009, 40(1): 44-50. (in Chinese)) |
| [5] |
张国新, 刘毅, 李松辉, 等. "九三一"温度控制模式的研究与实践[J]. 水力发电学报, 2014, 33(2): 179-184. ( ZHANG Guoxin, LIU Yi, LI Songhui, et al. Research and practice of Nine-Three-One temperature control mode[J]. Journal of Hydroelectric Engineering, 2014, 33(2): 179-184. (in Chinese)) |
| [6] |
朱岳明, 徐之青, 贺金仁. 混凝土水管冷却温度场的计算方法[J]. 长江科学院院报, 2003, 20(2): 19-21. ( ZHU Yueming, XU Zhiqing, HE Jinren. A calculation method for solving temperature field of mass concrete with cooling pipes[J]. Journal of Yangtze River Scientific Research Institute, 2003, 20(2): 19-21. (in Chinese)) |
| [7] |
黄耀英, 周宜红. 两种不同水管冷却热传导计算模型相关性探讨[J]. 长江科学院院报, 2009, 26(6): 56-59. ( HUANG Yaoying, ZHOU Yihong. Correlation of conduction calculation model for two different cooling pipes heat[J]. Journal of Yangtze River Scientific Research Institute, 2009, 26(6): 56-59. (in Chinese)) |
| [8] |
黄耀英, 周宜红, 周建兵. 水管冷却热传导计算模型能量分析[J]. 水利水运工程学报, 2012(1): 78-82. ( HUANG Yaoying, ZHOU Yihong, ZHOU Jianbing. Energy analysis of a pipe cooling thermal conduction calculation model[J]. Hydro-Science and Engineering, 2012(1): 78-82. (in Chinese)) |
| [9] |
朱伯芳, 蔡建波. 混凝土坝水管冷却效果的有限元分析[J]. 水利学报, 1985(4): 27-36. ( ZHU Bofang, CAI Jianbo. FEM analysis of effectiveness of water-cooling pipes embedded in concrete dams[J]. Journal of Hydraulic Engineering, 1985(4): 27-36. (in Chinese)) |
| [10] |
黄耀英, 郑宏, 夏开文, 等. 基于等效时间的混凝土水管冷却等效热传导[J]. 华中科技大学学报(自然科学版), 2012, 40(2): 45-48. ( HUANG Yaoying, ZHENG Hong, XIA Kaiwen, et al. Study on equivalent heat conduct of concrete using pipe cooling and equivalent time[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2012, 40(2): 45-48. (in Chinese)) |
| [11] |
朱伯芳. 有限单元法原理与应用[M]. 北京: 中国水利水电出版社, 1998. ( ZHU Bofang. Principle and application of finite element method[M]. Beijing: China Electric Power Press, 1998. (in Chinese))
|
 2017
2017 
