2. 河海大学水利水电学院, 江苏南京 210098;
3. 镇江市丹徒区航道管理处, 江苏镇江 212100
裂缝是水利工程病害中最常见形式,结构性裂缝因其延伸扩展严重影响水工建筑物安全,微裂纹(裂纹宽度极小或是处于闭合状态,分布于结构表面或内部,肉眼难以识别)是结构性裂缝的先兆,尽早发现微裂纹,可实现以可控方式主动释放水利工程安全风险。
选择性激励红外热像检测技术通过激振器激振混凝土结构,结构中的微裂纹受激振作用在尖角处会接触碰撞,进而出现显著温升,使用热像仪捕捉结构温度场,通过找寻显著温升区来发现微裂纹。已证明该技术可以有效发现混凝土结构中的微裂纹,但激励效果微弱[1-2],这成为限制该项新技术推广应用的瓶颈。当以结构固有频率作为激励频率对该结构进行激振时,将处于共振状态,在相同激励功率条件下,结构体的振幅最大[3]。大振幅增加了微裂纹处质点发生接触碰撞的可能,较多质点的接触碰撞有助于增强激励效果[4]。但当结构整体共振时,激振力会在结构内部产生波动,这两种振动彼此作用,共同影响着最终的激励效果;通过控制激振频率,探究整体振动与质点波动对热激励效果的影响以及彼此间的作用规律,这将有助于科学地增强选择性激励红外热成像检测技术的激励效果。
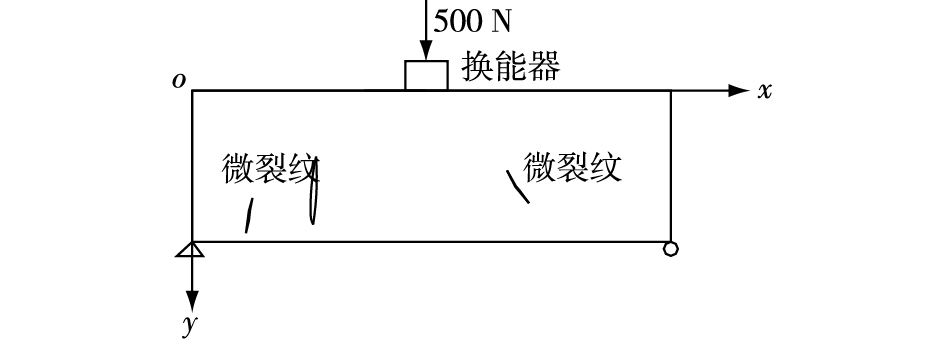
1 试验研究 1.1 建立简化模型并测定简支梁自振频率选用混凝土简支梁结构形式,将换能器置于梁跨中,加500 N压力于换能器,换能器质量0.02 kg。模型梁尺寸为:80 mm×80 mm×420 mm (y,z,x),混凝土强度等级C25,弹性模量E=2.8×104 N/mm2,泊松比ν=0.2,密度ρ=2 500 kg/m3,梁质量6.72 kg。声波在混凝土中传播速度v=3.8 km/s。假定混凝土均质、各向同性。微裂纹主要分布于梁内靠近上下表面处,模型如图 1所示。
|
图 1 含微裂纹的混凝土简支梁模型 Figure 1 Model for simply supported concrete beam containing micro cracks |
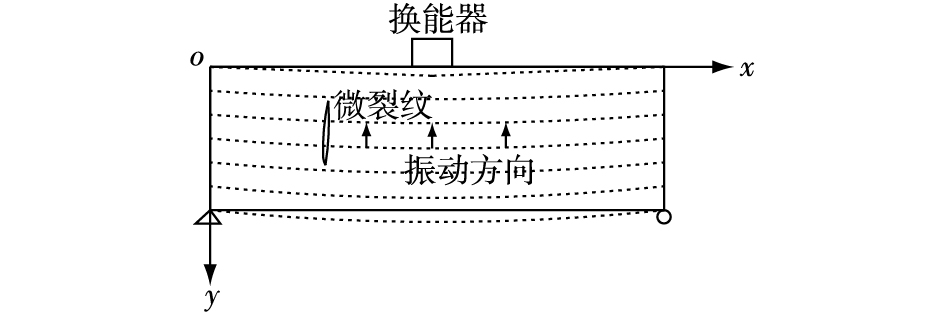
在简谐激振力作用下,简支梁整体振动振型如图 2虚线,因其跨高比大于5,故按欧拉梁模型计算。曲线上质点沿y轴方向在平衡位置上下作往复振动。设振动中梁的动挠度曲线为y (x, t),则y (x, t)=yc3x/l-4x/l3,0≤x≤1/2;其中yc是梁跨中的挠度,振动时是时间的函数,yc=yc(t)。
|
图 2 简谐激振下简支梁整体振动振型 Figure 2 Overall vibration chart of simply supported beam under harmonic excitation |
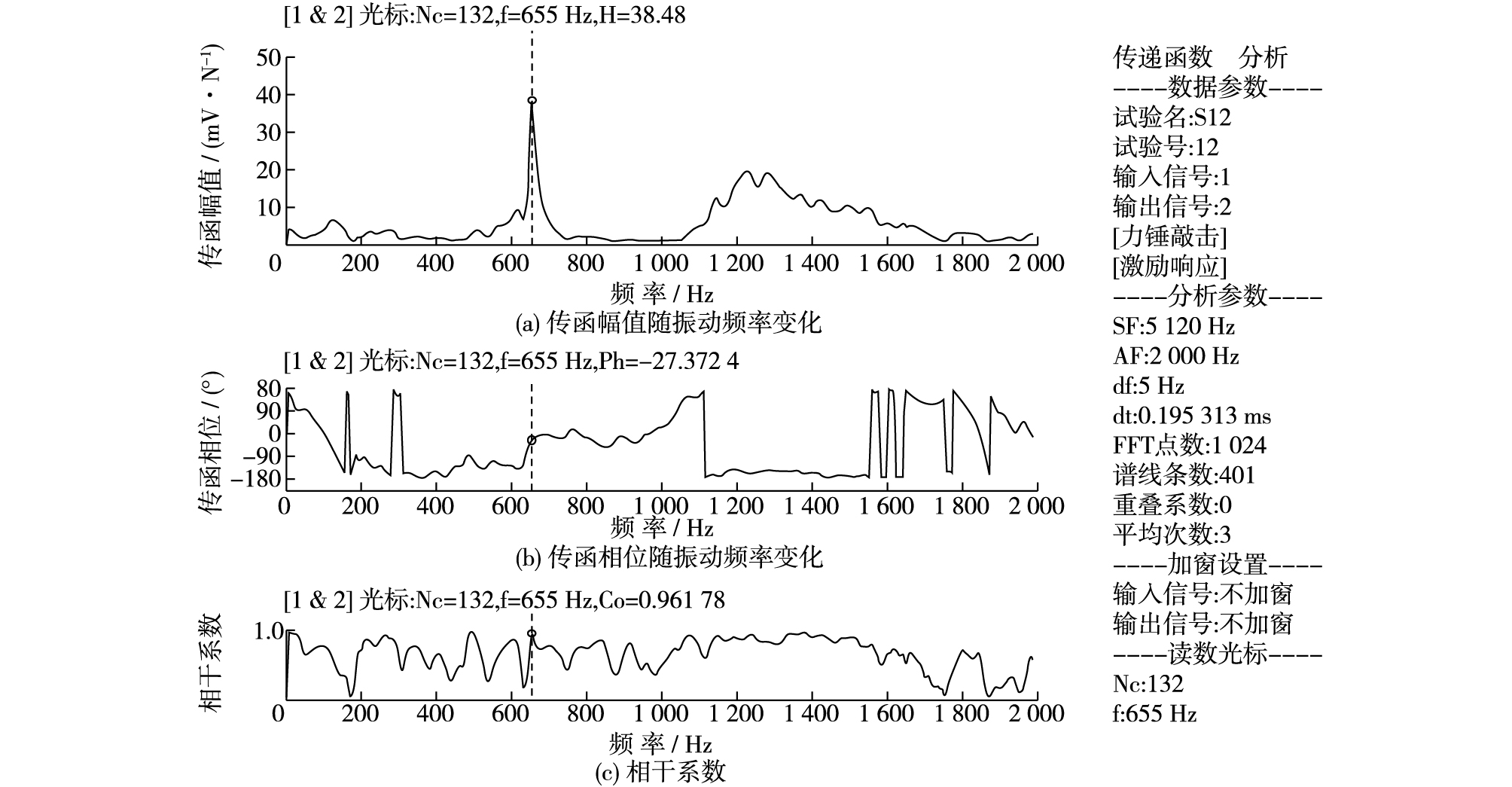
使用锤击法测实际简支梁自振频率。选用INV306U智能信号采集处理分析系统、CA-YD-107型加速度传感器、力传感器、INV-8型多功能抗混滤波放大器、装有DASPV10的笔记本电脑进行测试。制作80 mm×80 mm×420 mm的混凝土试块,其内部有不定数量的微裂纹,将试块置于两根钢筋棒上;试块一侧面靠下边缘处涂双面胶,并紧靠此面放置两层混凝土构件,使得试块与混凝土构件于接触面下部粘接在一起,以此作试块纵向约束,构成简支。传函数法计算结果如图 3所示。经过测试可知简支梁自振频率为655 Hz。
|
图 3 传函数法计算结果 Figure 3 Calculation results given by transfer function method |
首先试验655 Hz激振效果,考虑到实测自振频率与真实值可能存在差异,补充了300~1 300 Hz (以100 Hz为步长,共11组)的激振试验,试验中量测的电路电流范围0.9~1.1 A,将输出频率作相应调整,其余步骤不变。具体试验步骤为:① 按前述方法制作80 mm×80 mm×420 mm的混凝土试块,并将试块纵向约束,构成简支。② 选用G30激振器,通过电脑中的振动发生软件控制其激振频率,频率可调范围150~18 000 Hz,将振动发生软件设置为输出655 Hz的正弦激振力;选用KONESAV-338功率放大器增强激振器的激振强度。③ 用钳形表量测电路中的工作电流。④ 用压力传感器量测施加在换能器上的压力。⑤ 将换能器置于构件中间、表面整洁、完整处,用压力钳施加500 N压力于换能器;用红外热像仪记录构件内温度场变化;接通电路进行试验,钳形表读数1.0 A。
为充分降低激振中简支梁整体振动强度,同时避免高频率声波传播中衰减过快而影响在混凝土试件内的有效激励范围,选用超声频率40 kHz的试验激振效果, 试验步骤为:① 被激振构件同上,仍是简支结构。② 选用超声波发生器,输出频率40 kHz;用钳形表记录工作电流;用压力传感器量测施加在换能器上的压力。③ 将换能器置于构件中间、完整处,用压力钳施加500 N于换能器;用热像仪记录构件温度场变化;接通电路试验,钳形表读数0.5 A。
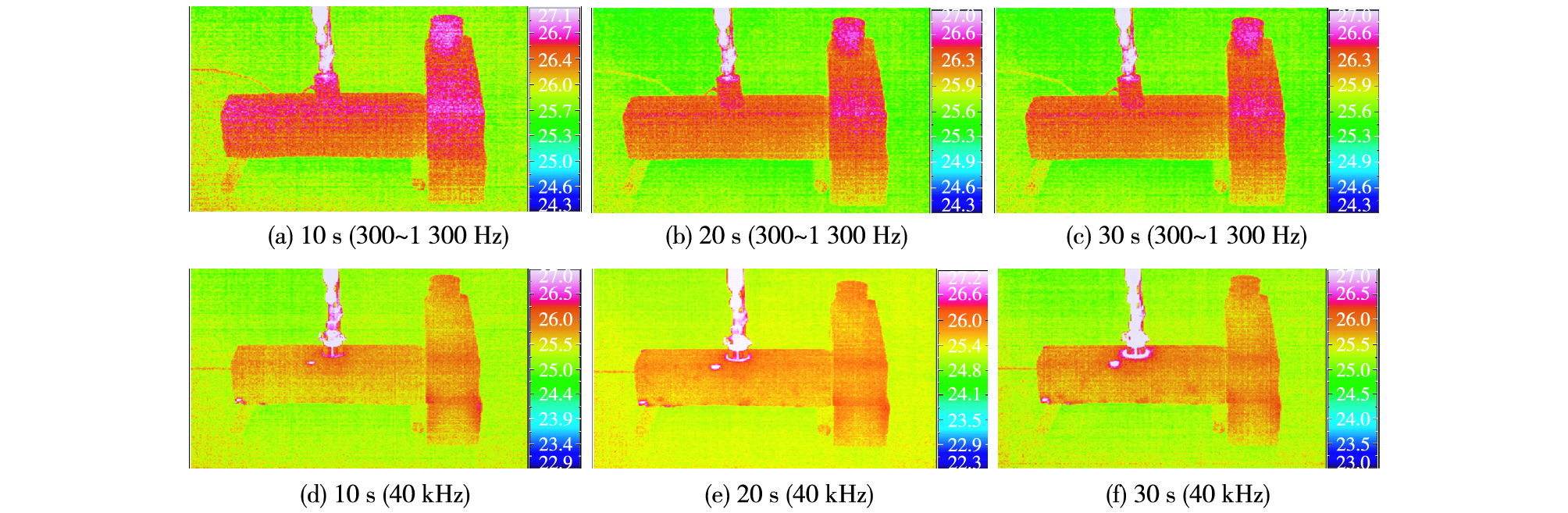
1.2.2 试验结果将300~1 300 Hz和40 kHz的试验结果进行汇总。由图 4可见,频率为300~1 300 Hz,10~30 s时简支梁均无明显温升;频率40 kHz,10 s时出现若干显著温升区,温升区最高温升1.0 ℃(环境温度27.7 ℃),20 s时温升区面积扩大、个数增多,温升区最高温升2.4 ℃,30 s时温升区面积进一步扩大、个数进一步增多,温升区最高温升2.4 ℃。
|
图 4 激振效果热像图分析 Figure 4 Thermographs of excitation effect by frequency tests |
激振力作用下的简支梁同时响应出两种振动:宏观上构件整体振动、细观上构件内部质点波动。整体振动是指从结构动力学角度,构件在动力荷载作用下整体以某一固定振型振动[5],如图 5;质点波动指构件某点在激振源作用下,内部质点依照某一定频率及振形先后各自振动[6],如图 6。在激振过程中,两种振动形式综合影响微裂纹处的激励效果。
|
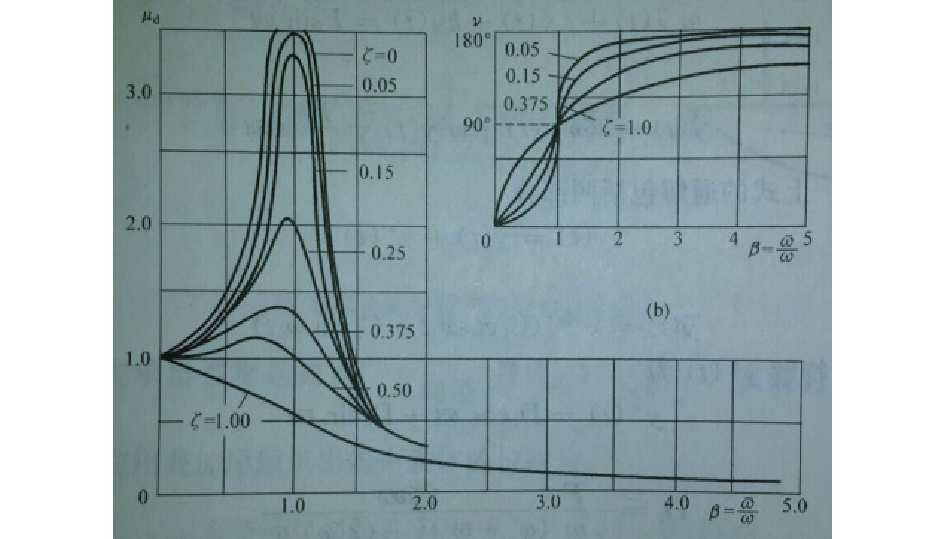
图 5 宏观整体振动的幅频响应曲线[3] Figure 5 Amplitude frequency response curves of macro overall vibration |

|
图 6 简谐激振下简支梁内部质点波形 Figure 6 Waveform graph of particles in simply supported beam under harmonic excitation |
为探究宏观整体振动与细观质点波动对微裂纹的激励能力强弱,首先确定简支梁共振状态下两种振动的剧烈程度。
2.1 简支梁处于结构共振状态时宏观外部动力响应简支梁跨中点在正弦激振力作用下的运动微分方程为:
| $ mx'' + cx' + kx = {F_0}\sin \omega t $ | (1) |
其特解为[7]:x=Bsin(ωt-φ),其中:B=βB0, B0为简支梁在激振力静作用下的最大位移;β为振幅放大因子,其值由图 5查得:混凝土相对阻尼比ξ=0.02[8],共振状态频率比λ=ω/ωn=1,故β=3.5。B0=Fl3/(48EI)=8.1 um, 因此,B=28 um。φ=tan-1(2ξλ/(1-λ2))=π/2。可知跨中点挠度为:
| $ {y_{\rm{c}}} = 0.028\sin \left( {4115t - {\rm{ \mathit{ π} /2}}} \right) $ | (2) |
则简支梁各点处动挠度曲线为:
| $ y\left( {x,t} \right) = 0.028\sin \left( {4115t - {\rm{ \mathit{ π} /2}}} \right)\left[ {3\left( {x/420} \right) - 4{{\left( {x/420} \right)}^3}} \right],0 \le x \le l/2 $ | (3) |
令y (x, t)对t求导,可知梁的振动速度为:
| $ v\left( {x,t} \right) = \cos \left( {4115t - {\rm{ \mathit{ π} /2}}} \right)\left( {0.87x - 6.57 \times {{10}^{ - 6}}{x^3}} \right) $ | (4) |
现求解简支梁整体以该速度振动1个周期所需能量:首先积分求解简支梁内所有质点在任意时刻t的动能总和:
| $ E\left( t \right) = m{v^2}\left( t \right)/2 = 2.38 \times {10^{ - 3}}{\cos ^2}\left( {4115t - {\rm{ \mathit{ π} /2}}} \right) $ | (5) |
简支梁在1个周期内振动所需能量
| $ \int_0^T {E\left( t \right){\rm{d}}t} = \sum\limits_{i = 0}^n {E\left( {{t_i}} \right)\Delta t} \left( {n\;趋于无穷大,\Delta t\;趋于无穷小} \right) $ | (6) |
那么
| $ {E_{\rm{T}}} = \sum\limits_{i = 0}^n {E\left( {{t_i}} \right)} = \frac{1}{{\Delta t}}\int_0^T {E\left( t \right){\rm{d}}t} = \zeta \int_0^T {E\left( t \right){\rm{d}}t} $ | (7) |
当E (t)>0时,总存在唯一定值ζ使得给定区间上的函数值累加和可用其面积积分表示。因此可知,ET=1.81×10-6ζ。
2.2 简支梁处于结构共振状态时细观内部动力响应因换能器相对于简支梁尺寸较小,波动距离受到简支梁尺寸限制,故简支梁中的波动按球面波考虑[9-10],质点波形及振动方向见图 6。由2.1节计算可知,距声源单位半径处(r=1 mm)球面波振幅28 um,ω=4 115 rad/s,长度统一以mm为单位计算,故质点波动方程为:
| $ y = 2.8 \times {10^{ - 2}}/r\sin \left( {4115t - \omega r/v} \right) $ | (8) |
式中:v为声波在混凝中传播速度;那么波振速度为:
| $ v\left( {r,t} \right) = {\rm{d}}y/{\rm{d}}t = 115.2/r\cos \left( {4115t - \omega r/v} \right) $ | (9) |
当半径取最大值r=0.21 m,ωr/v=0.07π时,相对于初始零相位其值可忽略不计,故近似认为简支梁内质点波振无相位差,即:
| $ v\left( {r,t} \right) = 115.2/r\cos \left( {4115t} \right) $ | (10) |
现求解简支梁内所有质点以该速度振动一个周期所需能量。首先积分求解所有质点在任意时刻t的动能总和:
| $ E\left( t \right) = 0.5\rho V{v^2} = 0.5\int_0^{210} {0.5\rho 4{\rm{ \mathit{ π} }}{r^2}{v^2}\left( {r,t} \right){\rm{d}}r} $ | (11) |
当100 mm < r≤210 mm时, 按球面积分的体积将有超出简支梁体积以外的部分,因简支梁中r>100 mm以外部分的波振速度相差较小,故用v (r=100, t)代替r>100 mm部分的质点任意时刻的波振速度,则总动能为:
| $ E\left( t \right) = 0.5\rho 0.5\int_0^{100} {4{\rm{ \mathit{ π} }}{r^2}v{{\left( {r,t} \right)}^2}{\rm{d}}r} + 0.5\rho \left( {V - 0.5\int_0^{100} {4{\rm{ \mathit{ π} }}{r^2}{\rm{d}}r} } \right)v{\left( {r = 100,t} \right)^2} $ | (12) |
代入数值可得:
| $ E\left( t \right) = 7.68 \times {10^{ - 6}}\left[ {\cos \left( {8230t} \right) + 1} \right] $ | (13) |
那么1个周期内简支梁所有质点波振所需能量为:
| $ {E_{\rm{T}}} = \zeta \int_0^T {E\left( t \right){\rm{d}}t} = \zeta \int_0^{1.53 \times {{10}^{ - 3}}} {7.68 \times {{10}^{ - 6}}\left[ {\cos \left( {8230t} \right) + 1} \right]{\rm{d}}t} = 1.18 \times {10^{ - 8}}\zeta $ | (14) |
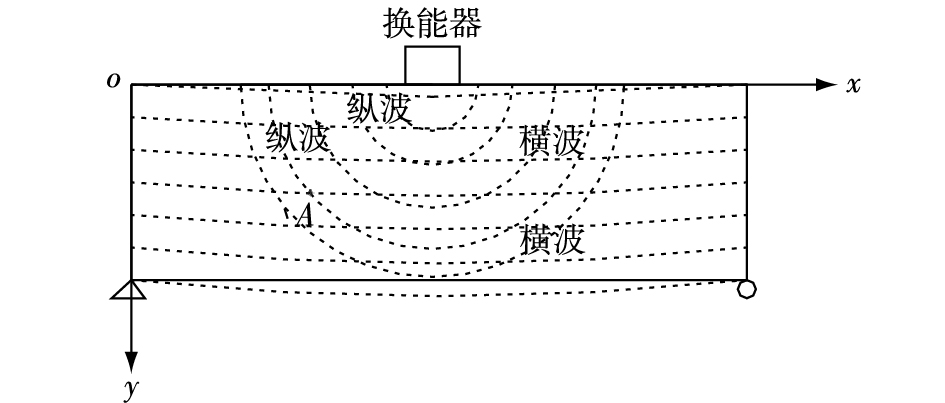
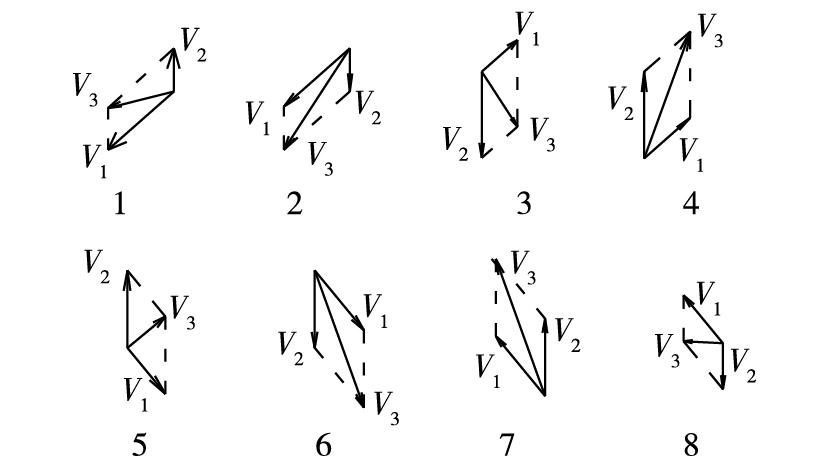
对比分析频率为655 Hz与40 kHz的试验结果。输出655 Hz的G30激振器,谐振阻抗为8 Ω,工作中电流为1 A;而输出40 kHz的换能器,谐振阻抗为20 Ω,工作中电流为0.5 A。由此可知,实际工作中G30激振器的输出功率大于40 kHz的换能器,可没有热激励效果。分析认为:这是宏观整体振动与细观质点波动共同作用的结果。简支梁在激振力作用下,振动形式见图 7,整个激振过程中,一方面结构整体沿纵向振型曲线上下持续振动;另一方面结构内部质点在球面波的带动下沿球面半径方向或球面切平面中某一方向交替振动,在简支梁中任取一点A,它在xoy平面内的实际速度合成共有8种代表形式,如图 8(1~4是整体振动与纵波波振的速度合成图,5~8是整体振动与横波波振的速度合成图,V1为纵波或横波波振速度,V2为整体振动速度,V3为实际振动速度)。下面从能量角度分析两种振动形式对激励效果的贡献及它们之间的相互影响规律。
|
图 7 简支梁在激振力作用下振动特征 Figure 7 Vibration chart of simply supported beam under harmonic excitation |
|
图 8 A点振动过程中实际速度合成 Figure 8 Actual speed composite image at point A under vibration |
对于655 Hz的激振试验,计算可得1个周期内简支梁整体振动储备了1.81×10-6ζ的能量,内部质点波动储备了1.18×10-8ζ的能量,质点波动强度远小于整体振动强度,质点波动对整体振动影响可忽略不计,故近似认为共振条件下简支梁仅处于整体振动状态;对于40 kHz的激振试验,激振频率是自振频率的58倍,由图 5可知整体振动振幅放大系数趋近于零,结构基本没有整体振动,近似认为简支梁仅处于细观质点波动状态;在相同压力作用、655 Hz换能器输出功率大于40 kHz换能器条件下,质点波动作用的梁出现了热激励效果,但整体振动作用的梁没有。因此可推知:整体振动对微裂纹的热激励能力弱于质点波动。这是因为,一方面,简支梁宏观整体振动方向为竖直方向,种类少于梁内细观质点波动方向,这使得整体振动作用下梁内微裂纹两侧质点发生碰撞的可能性低于质点波动作用的情况;另一方面,相邻质点间的波振存在相位差[11],即振动不同步且无序,而整体振动是同步、有序振动,这也影响了微裂纹两侧质点发生碰撞的可能性。
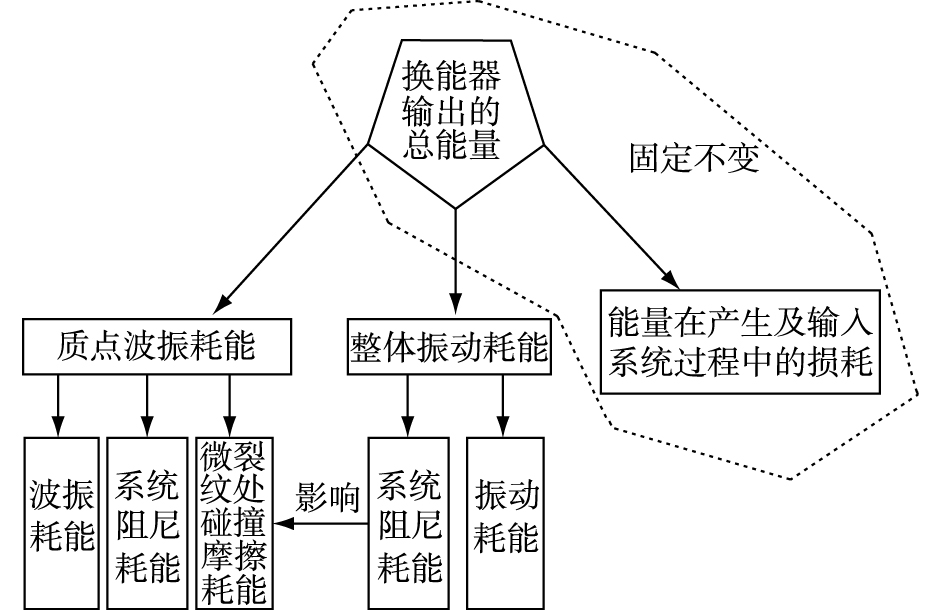
此外,换能器输出的总能量可认为流向3个方向:换能器自身消耗及换能器与简支梁在接触面处因振动摩擦消耗,记为E1;结构整体振动消耗,记为E2;结构内部质点波振消耗,记为E3;则E=E1+E2+E3,总能量分配如图 9。
|
图 9 换能器输出总能量分配 Figure 9 Distribution graph of transducer output energy |
振动过程中,在换能器输出功率一定的条件下,整体振动中阻尼耗能将消减换能器向质点波动提供的能量,这使得质点波动在微裂纹处耗能、阻尼耗能后,难以从换能器中得到充足的能量补充,振动强度因此衰减,进而减弱了质点波振发现微裂纹的能力。以655 Hz激振下的简支梁为例,当系统作稳态强迫振动时,1个周期内因激振力做功而从外界获得的能量等于阻尼消耗的能量[12]。1个周期激振力做功为:
| $ {W_f} = \int_0^T {F\left( t \right)v\left( t \right){\rm{d}}t} $ | (15) |
经化简可得[7]:
| $ {W_f} = {\rm{ \mathit{ π} }}B{F_0}\sin \varphi $ | (16) |
式中:F0为简支梁横截面上的剪力;φ为初始相位角;B为简支梁各横截面上振幅之和。现求解Wf,简支梁跨中受500 N压力,则F0=250 N;共振时φ=π/2,则
| $ \begin{array}{*{20}{c}} {B = \sum\limits_{i = 0}^n {B\left( {{x_i}} \right)} = \frac{1}{{\Delta x}}\int_0^l {B\left( x \right){\rm{d}}x} = }\\ {\zeta \int_0^l {B\left( x \right){\rm{d}}x} = 7.36 \times {{10}^{ - 6}}\zeta }\\ {{W_f} = 5.78 \times {{10}^{ - 3}}\zeta } \end{array} $ |
进而可知,共振下简支梁为维持其整体振动状态,1个周期振动需吸收5.78×10-3ζ的能量被阻尼消耗,这远高于质点波振1个周期的动能总量1.18×10-8ζ。
3 结语为探究整体振动、质点波动的热激励能力强弱,试验简支梁在自振频率655 Hz和40 kHz激振下的热激励效果。通过建立激振模型,结合试验现象,计算比较宏观整体振动、细观质点波动对微裂纹的热激励能力,并讨论了相关成因;分析了整体振动对质点波动的影响,结论如下:
(1) 构件在激振频率作用下,会同时响应出宏观整体振动与细观质点波动,宏观整体振动对微裂纹的热激励能力弱于细观质点波动,并会持续削弱细观质点的波振强度,弱化激励效果。
(2) 细观质点波动是激励效果出现的原因,可选用40 kHz超声频率激振来降低宏观整体振动强度,进而消除整体振动对质点波动强度的弱化作用。
| [1] |
汤雷, 蒋金平, 顾培英, 等. 超声红外法检测混凝土构件试验研究[J]. 水利学报, 2012, 43(增刊1): 70-75. ( TANG Lei, JIANG Jinping, GU Peiying, et al. Detect of concrete structures based on ultrasonic infrared thermal image with selective prompting[J]. Journal of Hydraulic Engineering, 2012, 43(Suppl1): 70-75. (in Chinese)) |
| [2] |
汤雷, 蒋金平. 超声红外热像技术进展及在混凝土应用的新探索[J]. 混凝土, 2012(3): 8-11, 14. ( TANG Lei, JIANG Jinping. Development of ultrasonic infrared thermography technology and the study on its application in concrete[J]. Concrete, 2012(3): 8-11, 14. (in Chinese)) |
| [3] |
张子明, 周星德, 姜冬菊. 结构动力学[M]. 北京: 中国电力出版社, 2009. ( ZHANG Ziming, ZHOU Xingde, JIANG Dongju. Structural dynamics[M]. Beijing: China Electric Power Press, 2009. (in Chinese))
|
| [4] |
徐维超. 超声红外热波无损检测技术应用于裂纹检测的研究[D]. 北京: 首都师范大学, 2008. (XU Weichao. Ultrasonic infrared thermal wave nondestructive evaluation for crack detection[D]. Beijing: Capital Normal University, 2008. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10028-2008144326.htm
|
| [5] |
李东旭. 高等结构动力学[M]. 北京: 科学出版社, 2010. ( LI Dongxu. Advanced structural dynamics[M]. Beijing: Science Press, 2010. (in Chinese))
|
| [6] |
弗伦奇A P. 振动与波[M]. 徐绪笃, 译. 北京: 人民教育出版社, 1981. (FRENCH A P. Vibrations and waves[M]. Translated by XU Xudu. Beijing: The People's Education Press, 1981. (in Chinese))
|
| [7] |
刘延柱, 陈立群, 陈文良. 振动力学[M]. 北京: 高等教育出版社, 2011. ( LIU Yanzhu, CHEN Liqun, CHEN Wenliang. Mechanics of vibration[M]. Beijing: Higher Education Press, 2011. (in Chinese))
|
| [8] |
柯国军, 郭长青, 胡绍全, 等. 混凝土阻尼比研究[J]. 建筑材料学报, 2004, 7(1): 35-40. ( KE Guojun, GUO Changqing, HU Shaoquan. Study on the damping ratio of concrete[J]. Journal of Building Materials, 2004, 7(1): 35-40. (in Chinese)) |
| [9] |
张治泰, 邱平. 超声波在混凝土质量检测中的应用[M]. 北京: 化学工业出版社, 2006. ( ZHANG Zhitai, QIU Ping. The application of ultrasonic in concrete quality detection[M]. Beijing: Chemical Industry Press, 2006. (in Chinese))
|
| [10] |
密士文. 混凝土中超声波传播机理及预应力管道压浆质量检测方法研究[D]. 长沙: 中南大学, 2013. (MI Shiwen. Study on mechanism of ultrasonic propagation in concrete and method of detecting grouting quality in pre-stressed tendon ducts[D]. Changsha: Central South University, 2013. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10533-1014395708.htm
|
| [11] |
王智丰, 周先雁, 晏班夫, 等. 冲击回波法检测预应力束孔管道压浆质量[J]. 振动与冲击, 2009, 28(1): 166-169, 190. ( WANG Zhifeng, ZHOU Xianyan, YAN Banfu, et al. Grout quality testing in prestressed ducts with impact echo method[J]. Journal of Vibration and Shock, 2009, 28(1): 166-169, 190. (in Chinese)) |
| [12] |
甘宜诚. 结构振动中阻尼理论模型探究及实验分析[D]. 长沙: 湖南大学, 2014. (GAN Yichen. Theoretical research and experimental analysis of structural damping[D]. Changsha: Hunan University, 2014. (in Chinese)) http://cdmd.cnki.com.cn/article/cdmd-10532-1014312068.htm
|
2. College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing 210098, China;
3. Waterway Management Office in Dantu County of Zhenjiang City, Zhenjiang 212100, China
 2017
2017 
