2. 中建海峡建设发展有限公司, 福建福州 350015
传统桩基设计一般采用确定性法或者概率法[1-3]:确定性设计采用整体安全系数来保证设计安全,易出现过度设计;可靠度设计将参数变异性考虑在内,却忽略了参数变异的不确定性,易降低设计安全度。由于传统设计中参数确定唯一的局限性,不能充分考虑岩土参数的不确性对单桩水平承载力的影响[4],以及水平荷载波动引起的水平承载力安全度稳定性降低问题。因此,采用确定性法或者概率法得到的设计方案,或偏保守或偏危险[5-6]。
鲁棒性设计[7]是一种通过调整“易于控制的设计参数”(桩几何尺寸、配筋率、混凝土强度等),降低因“难于控制的干扰因素”(岩土参数、水平荷载等)的不确定性引起的设计可靠度波动[8],保证设计方案安全稳定。本文采用鲁棒性设计方法,充分考虑岩土参数和水平荷载的不确定性,给出了单桩水平承载力鲁棒性设计方法与过程,并证明鲁棒性设计方法在单桩水平承载力设计中的适用性和合理性。基于可靠度方法的鲁棒性设计(RGD),作为一种新的设计方法用于单桩水平承载力设计,是对传统设计方法的补充与完善。
1 单桩水平承载力传统设计过程传统的单桩水平受力失效模式主要有挠曲失效模式(Deflection failure model, DFM)及强度失效模式(Strength failure model, SFM)两种[9],前者由桩顶水平位移过大引起,后者因桩控制截面弯矩过大造成,而桩土相互作用又影响两种失效模式。因此单桩水平承载力的传统设计方法中,需要明确设计中的目标函数、地基土模型和计算方法。
1.1 目标函数根据文献[9]提供的经验公式,建立关于水平受力桩的极限状态方程:
| $\left\{ \begin{array}{l} {g_1} = {y_{\rm{a}}} - {y_0}\\ {g_2} = {M_{\rm{U}}} - {M_{\max }} \end{array} \right.$ | (1) |
式中:ya为桩顶允许水平位移(本文取ya =6 mm); y0为桩顶水平位移;Mmax为桩身计算最大弯矩;MU为桩极限弯矩,根据文献[10]得:
| $\left\{ \begin{array}{l} \alpha {f_{{\rm{cm}}}}A\left( {1 - \frac{{\sin 2{\rm{ \mathsf{ π} }}\alpha }}{{2{\rm{ \mathsf{ π} }}\alpha }}} \right) + \left( {\alpha - {\alpha _{\rm{t}}}} \right){f_{\rm{y}}}{A_{\rm{s}}} = 0\\ M \le \frac{2}{3}{f_{{\rm{cm}}}}Ar\frac{{{{\sin }^3}{\rm{ \mathsf{ π} }}\alpha }}{\alpha } + {f_{\rm{y}}}{A_{\rm{s}}}{r_{\rm{s}}}\frac{{\sin 2{\rm{ \mathsf{ π} }}\alpha + \sin 2{\rm{ \mathsf{ π} }}{\alpha _{\rm{t}}}}}{{\rm{ \mathsf{ π} }}} \end{array} \right.$ | (2) |
式中:α为对应于受压区混凝土截面面积的圆心角与2π的比值;fcm为混凝土弯曲抗压强度设计值;αt为纵向受拉钢筋截面面积与全部纵向钢筋截面面积的比值,当α>0.625时,取αt=0;r为图形截面半径。为简化计算,采用徐文平等[10]提出的计算公式,具体见下式:
| ${M_{\rm{U}}} = 0.85{f_{\rm{y}}}{A_{\rm{s}}}{r_{\rm{s}}}$ | (3) |
式中:fy为钢筋屈服强度;As为钢筋面积;rs为钢筋所在圆的半径(取rs=(D-0.1) /2, 单位m)。
1.2 地基模型与计算方法引入Pasternak双参数地基模型[11],充分考虑土弹簧间的剪切作用,同时采用有限差分法分别考虑桩顶桩底边界条件,见图 1。

|
图 1 桩土计算模型 Figure 1 Model for pile and Pasternak foundation |
双参数地基模型的桩身挠曲微分方程:
| ${E_{\rm{p}}}{I_{\rm{p}}}\frac{{{{\rm{d}}^4}y}}{{{\rm{d}}{x^4}}} - GB\frac{{{{\rm{d}}^2}y}}{{{\rm{d}}{x^2}}} + Ky = 0$ | (4) |
式中:B为桩等效宽度(取B=0.9D, D为桩径);Ep为桩弹性模量;Ip 为桩截面惯性矩;地基土剪切刚度
| $K = \frac{{3.08}}{\eta }{\left( {\frac{{E{B^4}}}{{{E_{\rm{p}}}{I_{\rm{p}}}}}} \right)^{\frac{1}{8}}}\frac{E}{{\left( {1 - \nu _{\rm{s}}^2} \right)}}$ | (5) |
| $\eta = \left\{ \begin{array}{l} 2.18\;\;\;\;\left( {h/B \le 0.5} \right)\\ 1 + \frac{1}{{1.7h/B}}\;\;\;\left( {h/B \ge 0.5} \right) \end{array} \right.$ |
由有限差分法得:
| ${y_{i + 2}} - \left( {4 + \alpha } \right){y_{i + 1}} + \left( {6 + 2\alpha + \beta } \right){y_i} - \left( {4 + \alpha } \right){y_{i - 1}} + {y_{i - 2}} = 0$ | (6) |
式中:α=GB (Δx)2/(EpIp), β=K (Δx)4/(EpIp)。
桩顶自由边界条件:
| $\left\{ \begin{array}{l} {y_1} - 2{y_0} + {y_{ - 1}} = M{\left( {\Delta x} \right)^2}/\left( {{E_{\rm{p}}}{I_{\rm{p}}}} \right)\\ {y_2} - 2{y_1} + 2{y_{ - 1}} - {y_{ - 2}} = 2H{\left( {\Delta x} \right)^3}/\left( {{E_{\rm{p}}}{I_{\rm{p}}}} \right) \end{array} \right.$ | (7) |
桩顶嵌固边界条件:
| $\left\{ \begin{array}{l} \left( {{y_0} - {y_{ - 1}}} \right)/\Delta x = 0\\ {y_2} - 2{y_1} + 2{y_{ - 1}} - {y_{ - 2}} = 2H{\left( {\Delta x} \right)^3}/\left( {{E_{\rm{p}}}{I_{\rm{p}}}} \right) \end{array} \right.$ | (8) |
桩底自由边界条件:
| $\left\{ \begin{array}{l} {y_{n + 1}} - 2{y_n} + {y_{n - 1}} = 0\\ {y_{n + 2}} - 2{y_{n + 1}} + 2{y_{n - 1}} - {y_{n - 2}} = 0 \end{array} \right.$ | (9) |
将以上边界条件代入差分方程式(5),消去虚拟节点(-2, -1, n+1, n+2) 得到单桩水平位移方程为:
| $Y = {K^{ - 1}}F$ | (10) |
鲁棒性设计包括设计参数、不确定因素确定及概率设计方法选取。设计参数包括桩几何参数、桩身混凝土强度等,干扰因素主要是地基土参数,而概率性设计方法较多,常用的有一次可靠度方法和蒙特卡洛法。
2.1 设计参数设计参数包括桩的几何参数、桩身混凝土强度等,由文献可知长桩中桩径的增加对水平承载力贡献极大,而桩长的作用可以忽略。同时,桩身配筋率及混凝土强度对桩身强度的影响至关重要。因此,选择桩径、桩身配筋率与混凝土强度作为设计参数,桩径D=0.3~1.0 m,桩径每次增加0.05 m,桩身配筋率取0.8%,1.0%,1.2%,桩身混凝土强度取C30,C40,C50,而桩长固定为20 m。
将式(1) 作为水平桩承载力设计方案的目标函数,在挠曲失效模式和强度失效模式下的失效概率分别为PfDFM=Pr(QDFM < F)和PfSFM=Pr(QSFM < F),当设计失效概率小于给定的目标失效概率时,认为设计方案是合理的,即PfDFM < PT,PfSFM < PT,可靠度指标取2.7,即目标失效概率PT=0.003 5[13]。
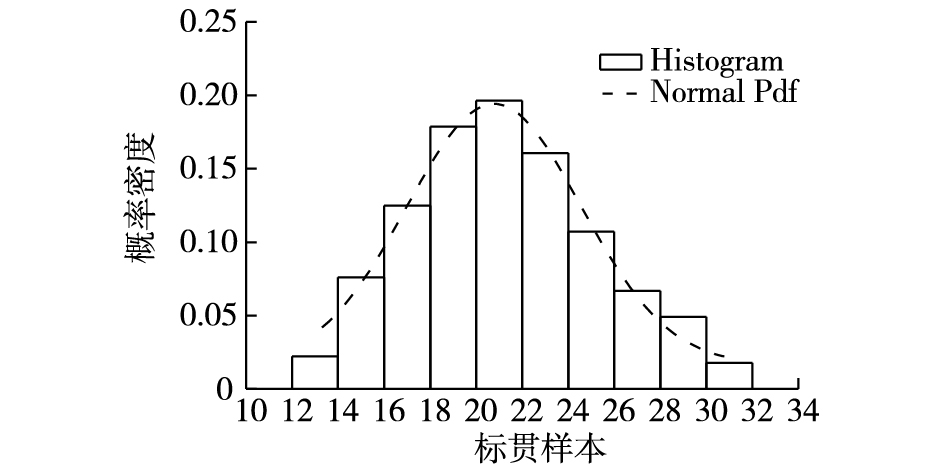
2.2 干扰因素的不确定性引起水平单桩承载力变化的不确定参数主要是土的剪切刚度G及地基反力模量K,而桩承担的水平荷载变化会引起设计承载力不足问题。研究表明土的剪切刚度G及地基反力模量K可由土的弹性模量推算,而土弹性模量可通过标准贯入试验确定,大量学者对标贯与土弹性模量间的关系进行了研究[14-15],采用日本建筑行业规范[16]中普遍使用的1.4N (N为标贯击数)作为土的弹性模量。图 2给出了某砂土的标贯数据[17]的概率分布型式。
|
图 2 某砂土标贯概率分布 Figure 2 Distribution of sand (SPT) |
桩的水平荷载一般由风荷载及地震等引起[18],概率分布一般为极值Ⅰ型分布,其密度函数:
| $f\left( {x;\mu ,\alpha } \right) = \alpha {{\rm{e}}^{ - \alpha \left( {x - \mu } \right) - {{\rm{e}}^{ - \alpha \left( {x - \mu } \right)}}}}$ | (11) |
积分得其分布函数:
| $F\left( {x;\mu ,\alpha } \right) = {{\rm{e}}^{ - {{\rm{e}}^{ - \alpha \left( {x - \mu } \right)}}}}$ | (12) |
式中:α为分位值;μ为随机变量x的平均值。
假设干扰因素见表 1。在实际工程中,尤其是岩土的标准贯入度可根据现场勘察结果进行调整。
| 表 1 干扰因素 Table 1 Parameters of noise factors |
为了解决干扰因素的不确定性问题即变异系数变化问题,一般情况下,参数平均值可通过有限样本数量测得,而一次取样测得参数的标准差为确定性结果,这与实际情况不符。Duncan[19-20]建议随机变量的平均值和标准差应通过变异系数(COV)计算或采用3-σ法估算得到。由文献可知:
| $\left\{ \begin{array}{l} {\mu _{{\rm{COV}}}} = \frac{{{H_{{\rm{COV}}}} + {L_{{\rm{COV}}}}}}{2}\\ {\sigma _{{\rm{COV}}}} = \frac{{{H_{{\rm{COV}}}} - {L_{{\rm{COV}}}}}}{4} \end{array} \right.$ | (13) |
式中:μCOV为变异系数平均值;σCOV为变异系数标准差;HCOV为变异系数上限;LCOV为变异系数下限。
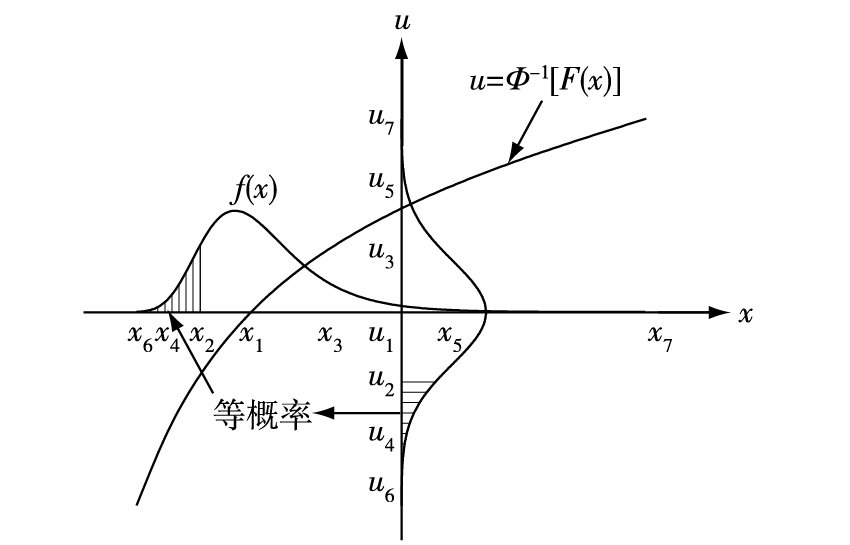
根据以上计算式计算得到岩土参数变异系数的平均值及标准差。然后采用Zhao等[21-22]提出的7点估计结合等概率代换,对干扰因素的变异系数进行估计,见图 3。图中根据7点估计法,通过等概率代换曲线u 将原随机变量概率密度函数f(x)上7个验算点xi (i=1, 2, 3, …, 7) 转换为标准状态分布函数中的7个估计点ui (i=1, 2, 3, …, 7)。
|
图 3 不确定参数变换 Figure 3 Uncertain parameters transformation |
单桩水平承载力鲁棒性设计流程如下:
① 选择设计参数、不确定因素和设计参数可选空间。为了弱化桩底边界条件的影响,固定桩长L=20 m,考虑桩径D(取0.3~1.0 m),配筋率ρ(在适筋范围取0.8%,1.0%,1.2%)以及桩身混凝土强度(C30,C40,C50) 3个设计参数(此处应说明,不同的建筑设计在设计参数的选择范围并不固定,应根据建筑场地及规范要求合理选择),确定土体的不确定因素,即标贯数据和水平荷载。
② 确定设计功能函数并计算设计方案的失效概率。将式(1) 中单桩水平承载力极限状态方程作为目标函数,利用可靠度设计方法计算得水平桩两种失效模式下的失效概率,同时利用式(7) 和(8) 考虑桩顶的边界条件,循环套用7点估计法并考虑变异系数的变化,结合蒙特卡洛法计算桩基失效概率的均值与标准差。
③ 建立外循环,重复②,计算所有设计方案失效概率的均值与标准差。
④ 优选设计结果。本例考虑将鲁棒性与可行性概率作为设计因素进行优选。
3 案例设计分析 3.1 可靠度设计可靠度设计要求干扰因素服从明确的统计规律,针对单桩水平承载力设计,假设干扰因素的变异系数估计准确,即采用表 1中的参数平均值及变异系数平均值,分别采用一次可靠度法和蒙特卡洛法计算某一确定性设计(桩径D=0.4 m,配筋率r=0.08%,C30混凝土)的单桩水平承载力的可靠度,见表 2。
| 表 2 一次可靠度与蒙特卡洛法计算的设计失效概率 Table 2 Failure probabilities of deterministic design by FORM and Monte Carlo simulation |
由表 2可知,一次可靠度法不适用于本例计算,而蒙特卡洛法虽然计算量大(单个参数模拟达百万次),但计算精度高,随着计算机及计算程序的升级优化,蒙特卡洛法的优势愈加明显。因此,对于单桩水平承载力的鲁棒性设计中可靠度计算方法采用蒙特卡洛法。
3.2 鲁棒性设计基于可靠度方法的鲁棒性设计可以充分考虑岩土参数等干扰因素的不确定性对岩土设计性能的影响,即采用目标失效概率筛选鲁棒性设计,将设计方案的失效概率变异性最小化。
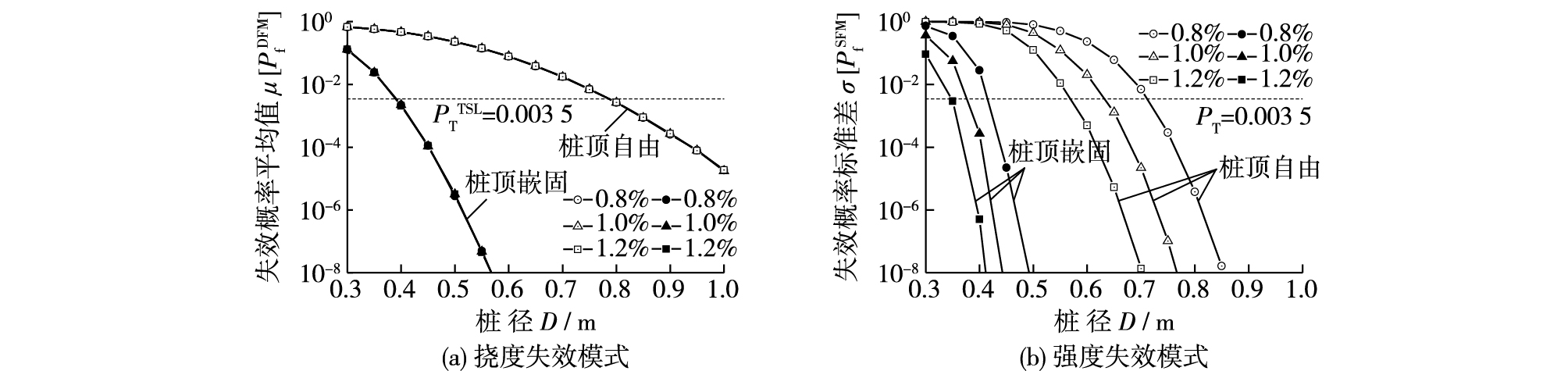
根据鲁棒性设计方法分别求出两种失效模式下的单桩水平承载力失效概率如图 4所示。首先,桩径的增加可有效提高桩抵抗水平荷载的能力;其次,配筋率大小仅对强度失效模式下的失效概率影响较大,这是由于桩身弯矩主要由钢筋承担的原因。由于桩顶嵌固的失效概率远小于桩顶自由状态,说明桩顶嵌固的单桩水平承载能力远高于桩顶自由状态。
|
图 4 鲁棒性设计方法计算的水平桩基失效概率 Figure 4 Probability of failure of laterally loaded pile obtained by RGD |
由图 4可知,满足挠度失效模式的最低要求设计分别为,桩顶自由时(D=0.8 m, ρ=0.08%),桩顶嵌固时(D=0.4 m, ρ=0.08%)。而确定性设计应根据下式:
| $R = {R_{{\rm{Ha}}}}/{F_{\rm{S}}}$ | (14) |
式中:R 为桩顶水平荷载;RHa为桩顶水平承载力;FS为安全系数(一般取FS=2)。
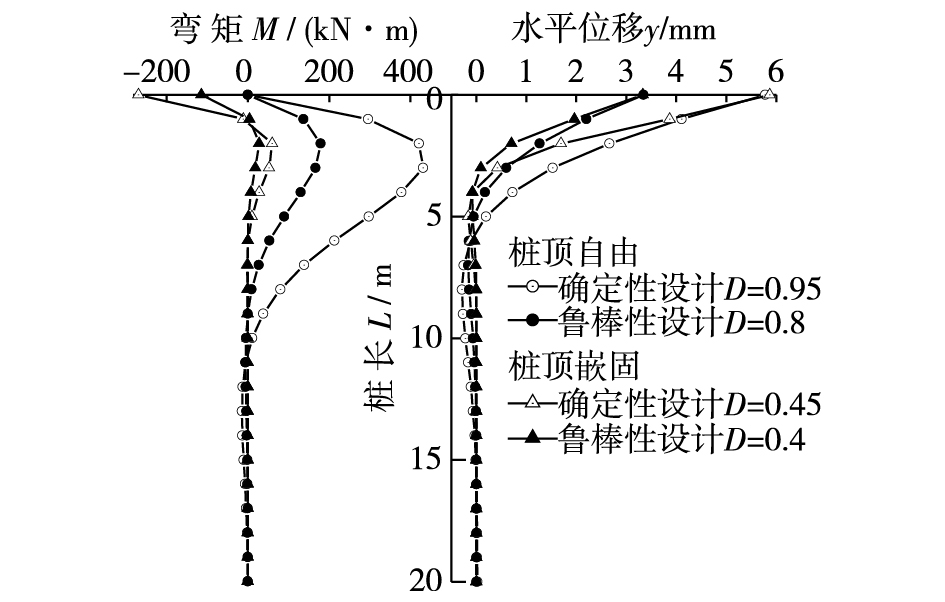
绘制确定性设计与鲁棒性设计下满足最低设计要求的桩身位移与弯矩,见图 5。满足目标失效概率的鲁棒性设计以较小的桩径即可满足设计要求,避免了确定性设计可能带来的不合理“过度设计”;同时鲁棒性设计基于可靠度方法,采用目标失效概率指导设计,又能保证设计安全性。
|
图 5 桩身位移与弯矩 Figure 5 Moment and displacement of laterally loaded pile |
为了考虑混凝土强度对单桩水平承载力的影响,固定配筋率为0.8%,计算挠度失效模式下3种混凝土强度的桩顶挠度失效概率,见图 6。由图 6(a)可知,提高混凝土强度可以减小桩顶水平位移,但是效果并不显著,在其他设计因素满足情况下,单纯提高混凝土强度抵抗桩顶水平位移会产生较高费用,经济性较差。

|
图 6 混凝土强度对水平桩鲁棒性设计的影响 Figure 6 Influence of concrete on laterally loaded pile obtained by RGD |
鲁棒性设计的结果是一个设计解集,其中涉及建筑基础造价,为了得到最优解,对设计造价简化计算,桩基造价按照单位体积桩基混凝土造价cc和单位质量的钢筋造价cb控制。C30, C40, C50混凝土的参考价格分别为335,345,365元/m3,钢筋参考价格为2 500元/t。作为经济性考虑的标准,具体见下式:
| $c = {c_{\rm{c}}} + {c_{\rm{b}}}$ | (15) |
由以上分析可知,混凝土强度控制挠度失效模式,配筋率控制强度失效模式,将满足目标失效概率的设计解集的标准差作为衡量设计方案的鲁棒性指标与造价作为双目标进行优化分析,建立针对桩顶自由和桩顶嵌固两种条件下的帕累托前沿(最优解的非支配解集),帕累托前沿上的设计既可以保证鲁棒性,同时具有较好经济性。关节点设计是同时具有最优鲁棒性与最优经济性的设计解,两者之间达到最佳平衡,关节点设计由下式计算得到:
| $\left\{ \begin{array}{l} \min \left( {\frac{{\sigma - {\sigma _{\min }}}}{{{\sigma _{\max }} - {\sigma _{\min }}}}{\lambda _1} + \frac{{c - {c_{\min }}}}{{{c_{\max }} - {c_{\min }}}}{\lambda _2}} \right)\\ {\lambda _1} = \left( {0,1} \right),{\lambda _2} = 1 - {\lambda _1} \end{array} \right.$ | (16) |
式中:σ为失效概率标准差,σmax,σmin分别为失效概率标准差中的最大值和最小值;c为造价,cmax,cmin分别为造价中的最大值和最小值;λ1, λ2为失效概率标准差和造价的权重系数。
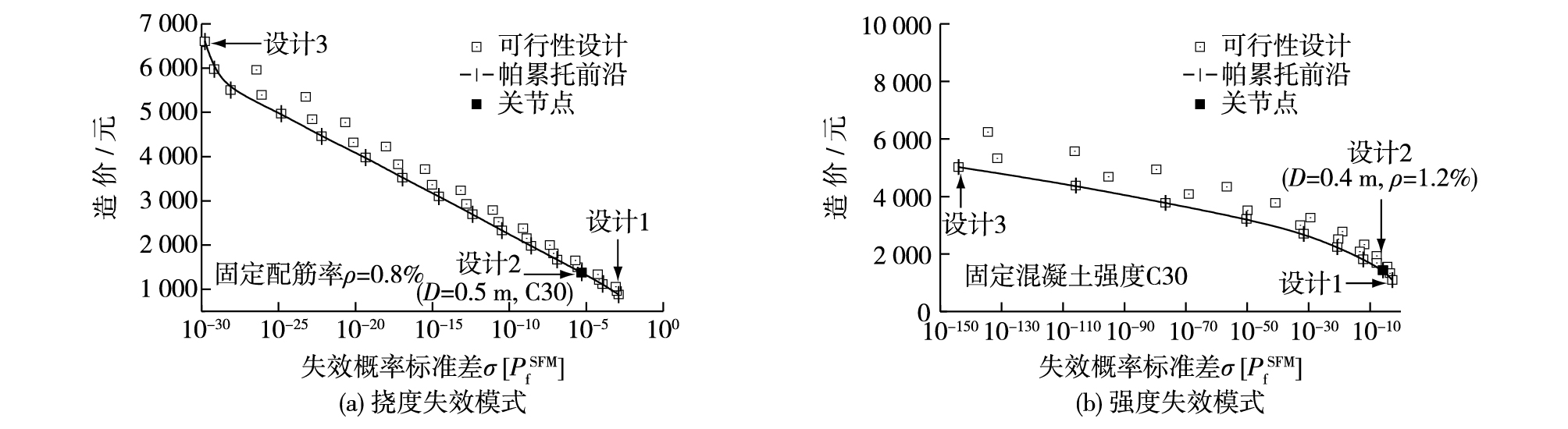
由图 7和8可知,失效概率标准差作为鲁棒性指标随着造价增加而显著降低,在帕累托前沿上的设计解集都是优化设计结果,设计1为帕累托前沿上造价最低,鲁棒性最高的设计,而设计3造价最高,鲁棒性最低,此两种极端设计,没有兼顾设计的其他方面,设计2(Knee point[23])作为帕累托前沿的关节点在造价与鲁棒性之间达到了平衡,被认为是最优设计方案。应当指出,特殊情况下,设计人员亦可采用权重系数法选择最优方案。

|
图 7 桩顶自由条件多目标优化 Figure 7 Multi-objective optimization of free-head laterally loaded pile |
|
图 8 桩顶嵌固条件多目标优化 Figure 8 Multi-objective optimization of fixed-head laterally loaded pile |
由以上分析可知,根据场地条件及规范要求合理选择设计参数范围,桩顶自由条件下,在保证桩顶水平位移安全性前提下,提高混凝土强度仅会增加安全度,而经济性较差,在适筋范围内适当加大桩径及配筋率可以显著提高桩身抵抗弯矩的能力;桩顶嵌固条件下较小桩径即可满足桩抵抗水平承载力的要求,提高桩身混凝土的经济性较差,而配筋率的加大可显著提高桩身抵抗弯矩的能力。
4 结语考虑岩土参数与水平荷载的不确定性,研究了单桩水平承载力鲁棒性设计方法,并将鲁棒性与经济性作为设计方案的评价标准对单桩水平承载力设计方案进行多目标优化,得出以下几点结论:
(1) 单桩水平承载力设计中岩土参数和水平荷载等干扰因素存在不确定性,其变异系数的波动往往造成参数的低估或高估导致设计结果偏于危险或偏于保守。鲁棒性设计可以充分考虑干扰因素变化对设计结果的影响,并可得到设计方案的稳定水平,是对传统设计方法补充与完善。
(2) 鲁棒性设计对设计参数的作用给出了明确评价,增加桩径与配筋率可以显著提高单桩水平承载力,桩身混凝土等级满足设计要求即可,否则造成浪费,经济性较差。
(3) 最低造价设计容易降低设计方案的安全性,过高考虑安全性的设计亦会增加经济成本,鲁棒性设计采用指标指导设计方案,结合多目标优化可以达到经济性与安全性的平衡。
(4) 桩顶边界条件影响桩身抵抗水平荷载能力,本文仅考虑了桩顶自由与桩顶嵌固两种状态,而路梁等桩顶铰接情况也应考虑,以降低因干扰因素不确定性引起的设计风险。
| [1] |
GB 50068—2001建筑结构可靠度设计统一标准[S]. (GB 50068—2001 Unified standard for reliability design of building structures[S]. (in Chinese))
|
| [2] |
GB 50007—2011建筑地基基础设计规范[S]. (GB 50007—2011 Code for design of building foundation[S]. (in Chinese))
|
| [3] |
郑建国, 张苏明, 吴世明. 桩基承载力概率分析的贝叶斯方法[J]. 岩土工程技术, 1999(2): 34-38. ( ZHENG Jianguo, ZHANG Suming, WU Shiming. The Bayesian method for the probability analysis of bearing capacity of the pile foundation[J]. Geotechnical Engineering Technique, 1999(2): 34-38. (in Chinese)) |
| [4] |
AMUNDARAY J I. Modeling geotechnical uncertainty by bootstrap resampling[D]. West Lafayette: Purdue Univ, 1994.
|
| [5] |
罗云华, 傅旭东. 水平受力桩的可靠度分析[J]. 勘察科学与技术, 2004(1): 12-14, 43. ( LUO Yunhua, FU Xudong. Reliability analysis of laterally loaded piles[J]. Site Investigation Science and Technology, 2004(1): 12-14, 43. (in Chinese)) |
| [6] |
PHOON K K, KULHAWY F H, GRIGORIU M D. Reliability-based design of foundations for transmission line structures[R]. TR-105000. Palo Alto, Calif: Electric Power Research Institute, 1995.
|
| [7] |
黄宏伟, 龚文平, 庄长贤, 等. 重力式挡土墙鲁棒性设计[J]. 同济大学学报(自然科学版), 2014, 42(3): 377-385. ( HUANG Hongwei, GONG Wenping, ZHUANG Changxian, et al. Robust geotechnical design of gravity retaining wall[J]. Journal of Tongji University(Natural Science), 2014, 42(3): 377-385. (in Chinese)) |
| [8] |
BASMA A A. Risk-reduction factor for bearing capacity of shallow foundations[J]. Canadian Geotechnical Journal, 1994, 31(1): 12-16. DOI:10.1139/t94-002 |
| [9] |
CHANC L, LOW B K. Reliability analysis of laterally loaded piles involving nonlinear soil and pile behavior[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(2): 431-443. |
| [10] |
徐文平, 孟少平. 圆形截面钢筋混凝土受弯构件正截面承载力的快速实用计算方法[J]. 工业建筑, 1997, 27(2): 43-45. ( XU Wenping, MENG Shaoping. A fast practical method to calculate the bearing capacity of RC flexural members with round section[J]. Industrial Construction, 1997, 27(2): 43-45. (in Chinese)) |
| [11] |
梁发云, 李彦初, 黄茂松. 基于Pasternak双参数地基模型水平桩简化分析方法[J]. 岩土工程学报, 2013, 35(增刊1): 300-304. ( LIANG Fayun, LI Yanchu, HUANG Maosong. Simplified method for laterally loaded piles based on Pasternak double-parameter spring model for foundations[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(Suppl1): 300-304. (in Chinese)) |
| [12] |
俞剑, 张陈蓉, 黄茂松. 被动状态下地埋管线的地基模量[J]. 岩石力学与工程学报, 2012, 31(1): 123-132. ( YU Jian, ZHANG Chenrong, HUANG Maosong. The subgrade modulus of underground pipelines subjected to soil movements[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(1): 123-132. (in Chinese)) |
| [13] |
JGJ 94—2008建筑桩基技术规范[S]. (JGJ 94—2008 Technical code for building pile foundations[S]. (in Chinese))
|
| [14] |
赖琼华. 岩土变形模量取值研究[J]. 岩石力学与工程学报, 2001, 20(增刊1): 1750-1754. ( LAI Qionghua. The research of the soil deformation modulus[J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(Suppl1): 1750-1754. (in Chinese)) |
| [15] |
张昆, 郭菊彬. 花岗岩残积土及全风化土标贯击数的概率分布[J]. 铁道工程学报, 2008, 25(2): 6-8, 25. ( ZHANG Kun, GUO Jubin. Probility distribution of measure standard penetration test of granite residual soil and completely rotten soil[J]. Journal of Railway Engineering Society, 2008, 25(2): 6-8, 25. (in Chinese)) |
| [16] |
TANAHASHI H. Formulas for an infinitely long Bernoulli-euler beam on the pasteranak model[J]. Soils and Foundations, 2004, 44(5): 109-118. DOI:10.3208/sandf.44.5_109 |
| [17] |
黄涛. 一种用标贯击数直接确定粉土、砂土压缩模量的方法[J]. 勘察科学技术, 1997(5): 11-14. ( HUANG Tao. A method of direct determination of the compression modulus of silt and sand using SPT blow counts[J]. Site Investigation Science and Technology, 1997(5): 11-14. (in Chinese)) |
| [18] |
PHOON K K, KULHAWY F H, GRIGORIU M D. Development of a reliability-based design framework for transmission line structure foundations[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2003, 129(9): 798-806. DOI:10.1061/(ASCE)1090-0241(2003)129:9(798) |
| [19] |
DUNCAN J M. Factors of safety and reliability in geotechnical engineering[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2000, 126(4): 307-316. DOI:10.1061/(ASCE)1090-0241(2000)126:4(307) |
| [20] |
CHERUBINI C. Closure to factors of safety and reliability in geotechnical engineering[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2001, 127(8): 700-721. DOI:10.1061/(ASCE)1090-0241(2001)127:8(700) |
| [21] |
ZHAO Y G, ONO T. New point estimates for probability method[J]. Journal of Engineering Mechanics, 2000, 126(4): 433-436. DOI:10.1061/(ASCE)0733-9399(2000)126:4(433) |
| [22] |
苏永华, 王奇山, 梁斌. 基于七点估计法的边坡稳定可靠度求解[J]. 郑州大学学报(工学版), 2010, 31(6): 14-18. ( SU Yonghua, WANG Qishan, LIANG Bin. Based on the seven point estimation method of slope stability reliability solution[J]. Journal of Zhengzhou University(Engineering Science), 2010, 31(6): 14-18. (in Chinese)) |
| [23] |
BRANKE J, DEB K, DIEROLF H, et al. Finding knees in multi-objective optimization[C]//Proc 8th Conf on Parallel Problem Solving from Nature (PPSN Ⅷ): Lecture Notes in Computer Science, 2004: 722-731.
|
2. CSCEC Strait Construction and Development Co., Ltd., Fuzhou 350015, China
 2017
2017 
