2. 合肥工业大学水资源与环境系统工程研究所,安徽合肥 230009;
3. 安徽省水利部淮河水利委员会水利科学研究院安徽省水利水资源重点实验室,安徽蚌埠 233000;
4. 安徽工程大学建筑工程学院,安徽芜湖 241000
干旱是指在某地理范围内自然供水源一定时期持续少于某一临界值而导致的水分亏缺现象,当干旱达到一定程度后导致供水匮乏,对作物生长、人类生产生活和生态环境造成不利影响的事件即为旱灾[1-2],这些干旱不利影响的不确定性就是旱灾风险。旱灾风险可看作是一个复杂系统[2]:由致灾因子危险性、承灾体暴露、灾损敏感性和防灾减灾能力等四部分组成,其中后三者称为承灾体的脆弱性。目前,国内外关于灾害风险定量评估普遍接受的是“灾害风险=致灾因子危险性+承灾体脆弱性”理论[3-4]。致灾因子危险性主要与降水、气温等自然因素有关,可预见但难控制;承灾体脆弱性既有自然属性也有社会属性,目前主要是通过降低脆弱性才能有效减小旱灾风险。可见,农业旱灾系统脆弱性评价在农业旱灾风险调控、管理中具有非常重要意义。蚌埠市地处安徽省东北部,属亚热带季风气候与温带季风气候的过渡带、湿润带与半湿润带的过渡带,旱涝灾害频发,对农业生产影响严重[5]。评价蚌埠市农业旱灾系统脆弱性,有助于指导蚌埠市农业旱灾风险调控、管理,规避或减少农业旱灾损失。
水灾害系统风险产生的根本原因是系统中的不确定性[6]。旱灾风险评估中的不确定性主要是随机不确定性和模糊不确定性[1-2],这方面的不确定性计算主要有模糊综合评价、灰色系统、集对分析等。李德毅等[7-8]根据随机性、模糊性等不确定性的关联特征,提出了云模型,用定性定量相结合来表征不确定性。王贺等[9]将云模型用于自然灾害风险评估,计算了城市水灾风险的不确定性。张勇等[10]提出了相似云的概念以及度量分析方法,张仕斌等[11]将云相似度应用于风险评估中,进一步验证了云相似度用于风险评估的可行性和合理性。本文在上述研究基础上,拟采用改进的云相似度方法进行蚌埠市农业旱灾系统脆弱性评价,定量分析旱灾脆弱性系统的不确定性。
1 云模型及其相关概念 1.1 云滴及参数设U为一个定量论域,C是U上的定性概念,若x∈U,且x是C的一次随机实现,确定度μ定义为
| $ \mu :U \to \left[ {0,1} \right]\;\;\;\;\forall x \in U\;\;\;x \to \mu \left( x \right) $ |
x在论域上的分布μ(x)称为云,每一个(x, μ)为一个云滴。云用期望Ex、熵En和超熵He这3个参数来定量表征一个定性概念。期望Ex是云滴在论域空间的平均值;熵En是定性概念的不确定性度量,类似于标准差;超熵He是熵的熵,又称二次熵[7-8, 12]。
1.2 云发生器云发生器主要有正向正态云发生器和无需确定度信息的逆向云发生器。
(1) 正向正态云发生器[13]的输入为:云模型参数(Ex, En, He),云滴个数n;输出为n个云滴(xi, μi)。算法步骤为:① 以En为期望、He为标准差生成一个高斯随机数Eni';② 以Ex为期望、Eni'为标准差生成一个高斯随机数xi;③ 计算μi=exp[-(xi-Ex)2/(2Eni'2)];④ 得到数域中的一个云滴(xi, μi);⑤ 重复步骤① 至④,得到n个云滴。
(2) 无需确定度信息的逆向云发生器[14]的输入为:样本点xi,其中i=1, 2, …, n;输出为:云模型参数(Ex, En, He)。算法步骤为:① 根据xi计算均值
张国英等[15]将两个云的距离定义为:
| $ d\left( {{X_{ik}},{X_{jk}}} \right) = \left\{ \begin{array}{l} 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{X_{ik}} \subseteq {X_{jk}}\;或\;{X_{ik}} \supseteq {X_{jk}}\\ \frac{{\left| {E{x_{ik}} - E{x_{jk}}} \right|}}{{3\left( {{e_{ik}} + {e_{jk}}} \right)}}\;\;\;\;\;\;{X_{ik}} \not\subset {X_{jk}}\;或\;{X_{jk}} \not\subset {X_{ik}} \end{array} \right. $ | (1) |
式中:
| $ S\left( {{X_{ik}},{X_{jk}}} \right) = \left\{ \begin{array}{l} 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;d\left( {{X_{ik}},{X_{jk}}} \right) = 0\\ 1 - d\left( {{X_{ik}},{X_{jk}}} \right)\;\;\;\;\;\;0 < d\left( {{X_{ik}},{X_{jk}}} \right) < 1\\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;d\left( {{X_{ik}},{X_{jk}}} \right) \ge 1 \end{array} \right. $ | (2) |
改进方法:由于Xmin与Xmax都是随机产生,无规律可循,有可能Xmax较小而Xmin较大则跨度小,或者Xmax较大而Xmin较小则跨度大,导致计算结果偏差较大;参照正态分布的3σ准则(拉依达准则),选取确定的参数(即,以x+3σ作为Xmax,以x-3σ作为Xmin),结合式(1) 的含义,两个云之间的距离定义为:
| $ d = \frac{{\left| {\bar X - \bar Y} \right|}}{{{\sigma _x} + {\sigma _y}}} = \frac{{\left| {E{x_x} - E{x_y}} \right|}}{{E{n_x} + E{n_y}}} $ | (3) |
相似度定义为:
| $ S = \left( {{d_{\max }} - d} \right)/\left( {{d_{\max }} - {d_{\min }}} \right) $ | (4) |
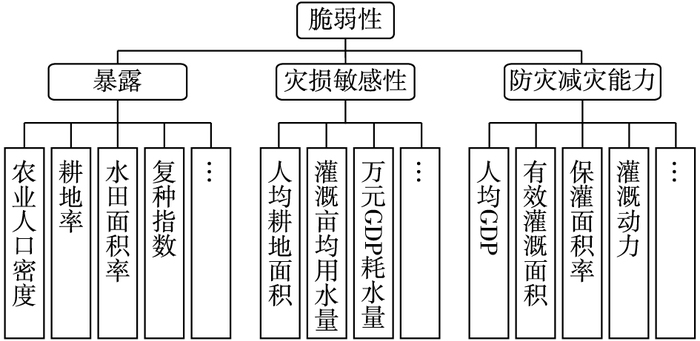
在分析影响农业旱灾系统脆弱性的自然条件与社会经济状况等基础上,依照指标体系的构建原则[16]建立由承灾体的暴露子系统(E)、灾损敏感性子系统(V)、防灾减灾能力子系统(A)等以及子系统下多项指标的农业旱灾系统脆弱性评价初步指标体系。利用AGA-AHP[17]方法求各子系统及各项指标的权重{wj,wj,k| j=1, 2, …, m; k=1, 2, …, nj},其中m,nj分别为农业旱灾系统脆弱性评价子系统数目、子系统j的评价指标数目。根据计算的权重值筛选初步指标体系,选取权重均值大、标准差小的指标组成最终的指标体系,见图 1。现分析图 1的合理性,如灾损敏感性子系统V中,农业灌溉亩均用水量指标越大,说明遇旱严重时损失越大,即灾损敏感性越大,其反映的脆弱性就越强;其他子系统指标类似。
|
图 1 农业旱灾系统脆弱性评价初步指标体系 Figure 1 Primary index system for agricultural drought vulnerability assessment |
根据前文所确定的统脆弱性评价指标体系中各指标与子系统的含义以及区域自然条件、社会经济状况等方面的因素,搜集整理安徽省17个地级市2001年至2010年的统计资料[18],建立农业旱灾系统脆弱性评价等级标准{sg,j,k| g=0, 1, 2, …, G; j=1, 2, …, m; k=1, 2, …, nj}(sg,j,k即为等级端点值),对应的评价指标样本值记为{xi,j,k| i=1, 2, …, N; j=1, 2, …, m; k=1, 2, …, nj}。其中,N,G分别为评价样本数、等级标准的等级数,m,nj同上。为了简便又不失一般性,约定这些等级中1级为“非常弱”,G级为“非常强”,中间等分;这里取G=5(g=1~5级农业旱灾系统脆弱性评价等级分别记为“弱”、“较弱”、“中”、“较强”和“强”)进行论述,其中s0, j,k与s1, j,k为等级1的端点值,其他等级及端点值以此类推。
2.3 基于云模型的单指标评价 2.3.1 指标体系样本值的云模型参数根据前述的无需确定度信息的逆向云发生器[13-14]算法,计算指标体系样本值的云模型参数(Exx,i,j,k,Enx,i,j,k,Hex,i,j,k),其中Exx,i,j,k=xi,j,k(指标样本值);Enx, 1, j,k=Enx, 2, j,k=…=Enx,N,j,k=Enx,j,k;Hex, 1, j,k=Hex, 2, j,k=…=Hex,N,j,k=Hex,j,k;Enj,k与Hej,k由逆向云发生器得到。
2.3.2 评价指标等级的云模型参数张秋文等[19]根据评价指标因素的云模型参数的不同计算方法,确定了评价指标等级的云模型参数,用以评价样本值与等级值之间的关系,即对样本值进行评价。参考文献[19]的方法,对评价指标等级的云模型参数(Exy,g,j,k,Eny,g,j,k,Hey,g,j,k)进行计算:
| $ E{x_{y,g,j,k}} = \left( {{s_{g,j,k}} + {s_{g + 1,j,k}}} \right)/2 $ | (5) |
| $ E{n_{y,g,j,k}} = \left( {{s_{g + 1,j,k}} - {s_{g,j,k}}} \right)/6 $ | (6) |
由于存在含混度[7]的概念,超熵的计算如下:
| $ H{e_{y,g,j,k}} = {\lambda _{y,g,j,k}} = \frac{1}{3}E{n_{y,g,j,k}} $ | (7) |
对于最低等级1与最高等级G分别采用半降正态云与半升正态云模型:当待评价指标值x小于等级1的均值Ex时,其属于等级1的隶属度为1;同理,当待评价指标值x大于等级G的均值Ex时,其属于等级G的隶属度为1;中间等级采用正态云模型。
通过比较指标样本值云参数(Exx, i, j, k,Enx, i, j, k,Hex, i, j, k)与指标等级云的参数(Exy, g, j, k,Eny, g, j, k,Hey, g, j, k)来反映样本值属于某个等级范围的情况,即反映农业旱灾系统脆弱性的强弱程度。其中Exx, i, j, k与Exy, g, j, k反映的是样本值属于某等级范围的大致情况,Enx, i, j, k与Eny, g, j, k反映云的跨度,即农业旱灾系统脆弱性的偏差程度,Hex, i, j, k与Hey, g, j, k反映的是云的厚度,即农业旱灾系统脆弱性的稳定性。
2.4 基于云相似度的综合评价 2.4.1 云相似度计算基于云模型进行单指标评价时,需比较(Exx, i, j, k,Enx, i, j, k,Hex, i, j, k)与(Exy, g, j, k,Eny, g, j, k,Hey, g, j, k),由于不同指标具有不同量纲和数量级,在初始资料没有进行归一化处理时,无法直接加权平均,按照式(3) 与(4) 的计算方法,进行基于改进云相似度的农业旱灾系统脆弱性综合评价,其距离为:
| $ {d_{i,g,j,k}} = \frac{{\left| {E{x_{x,i,j,k}} - E{x_{y,g,j,k}}} \right|}}{{E{n_{x,i,j,k}} + E{n_{y,g,j,k}}}} $ | (8) |
云相似度为:
| $ {S_{i,g,j,k}} = \frac{{{d_{\max ,i,j,k}} - {d_{i,g,j,k}}}}{{{d_{\max ,i,j,k}} - {d_{\min ,i,j,k}}}} $ | (9) |
式中:
结合前面得到的权重与各样本值与等级值之间的云相似度,运用层次分析法,计算各子系统以及整个农业旱灾风险系统的脆弱性等级云相似度。子系统与等级云之间的相似度为:
| $ {S_{i,g,j}} = \sum\limits_{k = 1}^{{n_j}} {{S_{i,g,j,k}}{w_{j,k}}} $ | (10) |
脆弱性系统与等级云之间的相似度为:
| $ {S_{i,g}} = \sum\limits_{j = 1}^m {{S_{i,g,j}}{w_j}} $ | (11) |
得到农业旱灾风险各子系统以及整个系统与各脆弱性等级云之间的相似度后,利用加速遗传算法(AGA)[20]对云相似度进行逆向运算优化,得到各子系统以及整个农业旱灾风险系统的云模型参数(Exx,i,j,Enx,i,j,Hex,i,j)与(Exx,i,Enx,i,Hex,i),并与旱灾系统脆弱性等级云模型参数(Exy, g,Eny, g,Hey, g)进行比较,以确定农业旱灾系统脆弱性的强弱程度。最终从样本单指标、子系统、整个农业旱灾风险系统3个层次对农业旱灾系统脆弱性进行评价,包括强弱程度、偏差程度、稳定性等因素,反映旱灾风险的不确定性。
3 模型应用在拟定指标选取原则基础上,确定蚌埠市农业旱灾系统脆弱性评价初步指标体系;然后经专家打分,采用AGA-AHP修正各判断矩阵的一致性并计算权重,筛选指标,得到最终指标体系见表 1左侧部分(子系统、各指标的名称及权重)。
| 表 1 农业旱灾系统脆弱性评价子系统与指标权重和评价等级 Table 1 Weights and assessment grades of agricultural drought disaster vulnerability system |
由于目前农业旱灾系统脆弱性等级没有统一的评价标准,因此本模型整理安徽省17个地级市2001—2010年的统计资料,按照等级划分原则将各指标的统计资料进行等级划分,由左至右分别等分为正(逆)序指标1~5级,详见表 1右侧部分(等级划分)。
计算蚌埠市农业旱灾系统脆弱性各评价指标每年数据的云模型参数(Exx,i,j,k,Enx,i,j,k,Hex,i,j,k)与每一等级的云模型参数(Exy, g, j, k,Eny, g, j, k,Hey, g, j, k),通过比较两个云来反映样本值属于某个等级范围的情况,即反映农业旱灾系统脆弱性的强弱程度、偏差程度、稳定性等。下面给出单指标脆弱性评价有代表性的样本值与等级值之间的几张云模型图。
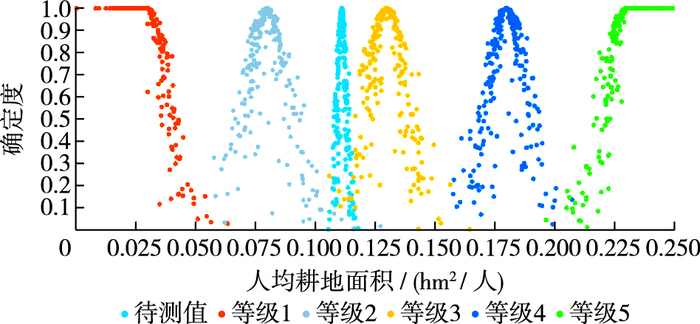
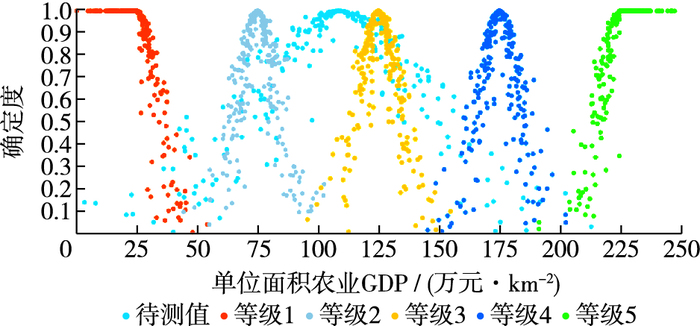
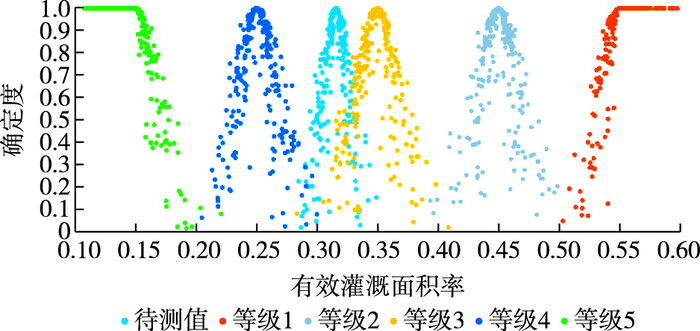
图 2说明2007年人均耕地面积反映蚌埠市农业旱灾系统脆弱性的评价结果,属于等级2~3,稍偏向等级3,且样本数据较为集中,云模型图较“窄”且“薄”,即不确定性较小,离散程度小、稳定性好。图 3说明2004年单位面积农业GDP反映蚌埠市农业旱灾系统脆弱性的评价结果,同样属于等级2~3,稍偏向等级3,但是样本数据较为分散,云模型图较“宽”且“厚”,即不确定性较大,离散程度大、稳定性差。图 4较为中等既不“窄”“薄”又不“宽”“厚”,说明2006年有效灌溉面积率反映蚌埠市农业旱灾系统脆弱性的评价结果,属于等级3与等级4之间,稍偏向等级3;其他指标评价脆弱性结果大致在等级3左右,云模型图有“宽厚”有“窄薄”,即其他指标识别的脆弱性不确定性有大有小,离散程度有大有小、稳定性有差有好。
|
图 2 2007年人均耕地面积(V1) 反映脆弱性评价结果 Figure 2 Assessment results of vulnerability reflected by per capita arable land area (V1) in 2007 |
|
图 3 2004年单位面积农业GDP(E7) 反映脆弱性评价结果 Figure 3 Assessment results of vulnerability reflected by unit area agriculture GDP (E7) in 2004 |
|
图 4 2006年有效灌溉面积率(A3) 反映脆弱性评价结果 Figure 4 Assessment results of vulnerability reflected by effective irrigation area ratio (A3) in 2006 |
综合评价时,由于不同指标具有不同的量纲和数量级,在初始资料没有进行归一化处理时,无法直接加权平均,采用上述云相似度改进计算方法,进行蚌埠市农业旱灾系统脆弱性综合评价。计算两个云之间的相似度,进而对云相似度进行加权平均,得到每个子系统与脆弱性等级之间云相似度以及整个农业旱灾风险系统与脆弱性等级之间的云相似度;然后对云相似度进行逆向运算优化,得到各子系统以及整个农业旱灾风险系统的云模型参数,并与脆弱性等级云模型参数进行比较,以确定农业旱灾系统脆弱性的强弱程度。将所得结果与模糊综合评价方法所得结果进行比较,见表 2。
| 表 2 评价方法比较 Table 2 Comparison of assessment methods |
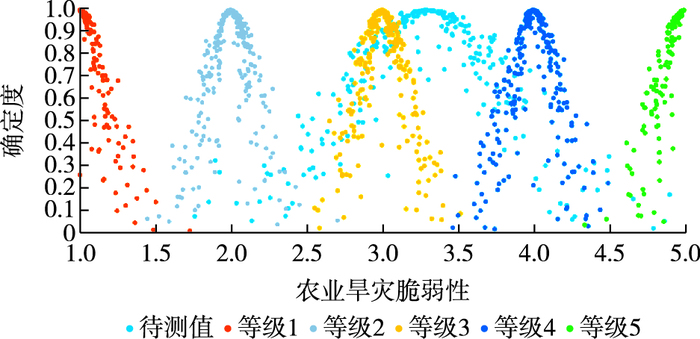
基于改进云相似度的评价方法所得的Ex与模糊综合评价结果表达的含义相同,将旱灾脆弱性描述为1~5的数值,数值越大则脆弱性越强。表 2数据表明,基于改进云相似度的评价方法所得的Ex与模糊综合评价结果大致相同,且偏小,即偏保守,同时又有En,He两个参数来反映可能取值范围、离散程度以及稳定性等不确定性,将脆弱性、风险等的不确定性考虑充分。图 5为基于此方法的蚌埠市2003年农业旱灾系统脆弱性评价结果。
|
图 5 基于云相似度的2003年蚌埠市农业旱灾系统脆弱性综合评价结果 Figure 5 Comprehensive assessment results of vulnerability of agricultural drought system of Bengbu city in 2003 based on cloud similarity |
图 5中:Ex反映了云的中心位置,表示脆弱性强弱程度的中心值,即2003年蚌埠市农业旱灾系统脆弱性属等级3~4,偏向于等级3(Ex=3.330);En反映了云的跨度,表示农业旱灾系统脆弱性的取值范围,即2003年蚌埠市农业旱灾系统脆弱性取值范围较大,可能原因是每个单指标评价的结果不同,导致综合评价结果方差较大,离散程度较大;He反映了云的厚度,即云的稳定性,表示脆弱性隶属度偏离其理论中心值的程度,即2003年蚌埠市农业旱灾系统脆弱性的云模型稳定性较差,这可能是每个单指标样本数据的方差较大,即方差的方差较大。该市其他年份的农业旱灾脆弱性评价结果类似2003年。
4 结语将农业旱灾脆弱性看作一个复杂系统,通过对每个评价指标的分析,可确定农业旱灾脆弱性不确定性的主要来源。传统评价方法仅考虑了确定性因素,得到了确定性结果,而往往忽略了不确定性,导致因忽略不确定性而使得评价结果的潜在风险愈渐突显。
利用云模型改进农业旱灾系统脆弱性综合评价模型,充分考虑了评价过程中存在的不确定性,并通过期望、熵和超熵3个参数将其表达出来,为定量分析农业旱灾系统脆弱性的不确定性提供了简便有效的方法;通过改进的云相似度方法进行农业旱灾系统脆弱性综合评价,可保留样本数据原有的数据特征,避免因数据归一化而造成的数据“失真”现象等。本文尝试将改进了云相似度计算方法应用于蚌埠市农业旱灾系统脆弱性评价中,取得了较好效果。同时,云模型是一种具有定性定量描述相互转换能力的模型,云相似度只是云模型的一种算法,如何将云模型更深入更广泛地应用到实际问题研究中,将是今后研究的一个重点。
| [1] |
金菊良, 宋占智, 崔毅, 等. 旱灾风险评估与调控关键技术研究进展[J]. 水利学报, 2016, 47(3): 398-412. ( JIN Juliang, SONG Zhanzhi, CUI Yi, et al. Research progress on the key technologies of drought risk assessment and control[J]. Journal of Hydraulic Engineering, 2016, 47(3): 398-412. (in Chinese)) |
| [2] |
金菊良, 郦建强, 周玉良, 等. 旱灾风险评估的初步理论框架[J]. 灾害学, 2014, 29(3): 1-10. ( JIN Juliang, LI Jianqiang, ZHOU Yuliang, et al. Research on theoretical framework of drought risk assessment[J]. Journal of Catastrophology, 2014, 29(3): 1-10. (in Chinese)) |
| [3] |
BLAKIC P, CANNON T, DAVIS I, et al. At risk: natural hazard, people's vulnerability and disasters[M]. Lond: Routledge, 1994.
|
| [4] |
刘兰芳, 刘盛和, 刘沛林, 等. 湖南省农业旱灾脆弱性综合分析与定量评价[J]. 自然灾害学报, 2002, 11(4): 78-83. ( LIU Lanfang, LIU Shenghe, LIU Peilin, et al. Synthetic analysis and quantitative estimation of the agricultural vulnerability to drought disaster in Hunan Province[J]. Journal of Natural Disasters, 2002, 11(4): 78-83. (in Chinese)) |
| [5] |
蚌埠市地方志编纂委员会. 蚌埠市志[M]. 北京: 方志出版社, 1995. ( The Local Chronicles Compilation Committee in Bengbu City. The chronicle of Bengbu City[M]. Beijing: Local Chronicles Publishing Company, 1995. (in Chinese))
|
| [6] |
左其亭, 吴泽宁, 赵伟. 水资源系统中的不确定性及风险分析方法[J]. 干旱区地理, 2003, 26(2): 116-121. ( ZUO Qiting, WU Zening, ZHAO Wei. Uncertainties in water resources system and risk analysis method[J]. Arid Land Geography, 2003, 26(2): 116-121. (in Chinese)) |
| [7] |
李德毅, 杜鹢. 不确定性人工智能[M]. 北京: 国防工业出版社, 2005. ( LI Deyi, DU Yi. Artificial intelligence with uncertainty[M]. Beijing: Publishing Company of National Defence Industry, 2005. (in Chinese))
|
| [8] |
LI Deyi, SHI Xuemei, WARD P, et al. Soft inference mechanism based on cloud models[C]//Proceedings of the 1st International Workshop on Logic Programming and Soft Computing: Theory and Application, Bonn, Germany, 1996.
|
| [9] |
王贺, 刘高峰, 王慧敏. 基于云模型的城市极端雨洪灾害风险评价[J]. 水利经济, 2014, 32(2): 15-20. ( WANG He, LIU Gaofeng, WANG Huimin. Urban extreme rainstorm flood loss based on cloud model[J]. Journal of Economics of Water Resources, 2014, 32(2): 15-20. (in Chinese)) |
| [10] |
张勇, 赵东宁, 李德毅. 相似云及其度量分析方法[J]. 信息与控制, 2004, 33(2): 129-132. ( ZHANG Yong, ZHAO Dongning, LI Deyi. The similar cloud and the measurement method[J]. Information and Control, 2004, 33(2): 129-132. (in Chinese)) |
| [11] |
张仕斌, 许春香, 安宇俊. 基于云模型的风险评估方法研究[J]. 电子科技大学学报, 2013, 42(1): 92-98. ( ZHANG Shibin, XU Chunxiang, AN Yujun. Study on the risk evaluation approach based on cloud model[J]. Journal of University of Electronic Science and Technology of China, 2013, 42(1): 92-98. (in Chinese)) |
| [12] |
李德毅, 刘常昱. 论正态云模型的普适性[J]. 中国工程科学, 2004, 6(8): 28-34. ( LI Deyi, LIU Changyu. Study on the universality of the normal cloud model[J]. Engineering Science, 2004, 6(8): 28-34. (in Chinese)) |
| [13] |
李德毅, 孟海军, 史雪梅. 隶属云和隶属云发生器[J]. 计算机研究与发展, 1995, 32(6): 15-20. ( LI Deyi, MENG Haijun, SHI Xuemei. Membership clouds and membership cloud generators[J]. Journal of Computer Research and Development, 1995, 32(6): 15-20. (in Chinese)) |
| [14] |
吕辉军, 王晔, 李德毅, 等. 逆向云在定性评价中的应用[J]. 计算机学报, 2003, 26(8): 1009-1014. ( LU Huijun, WANG Ye, LI Deyi, et al. The application of backward cloud in qualitative evaluation[J]. Chinese Journal of Computers, 2003, 26(8): 1009-1014. (in Chinese)) |
| [15] |
张国英, 沙芸, 余有明, 等. 基于属性相似度的云分类器[J]. 北京理工大学学报, 2005, 25(6): 499-503. ( ZHANG Guoying, SHA Yun, YU Youming, et al. Cloud classifier based on attribute similarity[J]. Transactions of Beijing Institute of Technology, 2005, 25(6): 499-503. (in Chinese)) |
| [16] |
邵立周, 白春杰. 系统综合评价指标体系构建方法研究[J]. 海军工程大学学报, 2008, 20(3): 48-52. ( SHAO Lizhou, BAI Chunjie. Index system construction on comprehensive evaluation[J]. Journal of Naval University of Engineering, 2008, 20(3): 48-52. (in Chinese)) |
| [17] |
金菊良, 魏一鸣, 丁晶. 基于改进层次分析法的模糊综合评价模型[J]. 水利学报, 2004, 3(3): 65-70. ( JIN Juliang, WEI Yiming, DING Jing. Fuzzy comprehensive evaluation model based on improved analytic hierarchy process[J]. Journal of Hydraulic Engineering, 2004, 3(3): 65-70. (in Chinese)) |
| [18] |
安徽省统计局, 国家统计局安徽调查总队. 安徽统计年鉴(2001—2015版)[M]. 北京: 中国统计出版社. ( Statistical Bureau of Anhui Province, Survey Office of the National Bureau of Statistics in Anhui. Anhui statistical yearbooks(from 2001 to 2015)[M]. Beijing: Statistics Publishing Company of China. (in Chinese))
|
| [19] |
张秋文, 章永志, 钟鸣. 基于云模型的水库诱发地震风险多级模糊综合评价[J]. 水利学报, 2014, 45(1): 87-95. ( ZHANG Qiuwen, ZHANG Yongzhi, ZHONG Ming. A cloud model based approach for multi-hierarchy fuzzy comprehensive evaluation of reservoir-induced seismic risk[J]. Journal of Hydraulic Engineering, 2014, 45(1): 87-95. (in Chinese)) |
| [20] |
金菊良, 杨晓华, 丁晶. 标准遗传算法的改进方案——加速遗传算法[J]. 系统工程理论与实践, 2001, 21(4): 8-13. ( JIN Juliang, YANG Xiaohua, DING Jing. An improved simple genetic algorithm——accelerating genetic algorithm[J]. System Engineering—Theory and Practice, 2001, 21(4): 8-13. (in Chinese)) |
2. Institute of Water Resources and Environmental Systems Engineering, Hefei University of Technology, Hefei 230009, China;
3. Key Laboratory of Water Conservancy and Water Resources of Anhui Province, Anhui and Huaihe River Institute of Hydraulic Research, Ministry of Water Resources, Bengbu 233000, China;
4. College of Civil Engineering and Architecture, Anhui Polytechnic University, Wuhu 241000, China
 2017
2017 
