2. 大连理工大学海岸和近海工程国家重点实验室,辽宁大连 116024
沙质海床广泛分布于近海海域,由不同粒径的泥沙颗粒组成,具有渗透性。当波浪在沙质海床上传播时,水质点会通过海床的孔隙渗流进海床内部,从而引起波高与波长的变化。Putman采用线性波浪理论,最先研究了波浪通过无限厚透水海床的问题,得出了海床的透水性会使波高衰减的结论[1]。Savage等先后通过试验研究了可渗透海床上的波浪衰减,发现波能消耗和波高衰减是底部摩阻和渗透造成的,且渗透系数较大的泥沙对波能的耗散相对显著[2-3]。Dean等基于线性波浪理论,推导得到了无限深常水深可渗透海床上波浪运动的速度势表达式和色散关系[4]。Silva等分别利用缓坡方程和Boussinesq方程研究了波浪在地形变化的渗透海床上传播时的波高分布[5-6]。唐志波等详细研究了不同渗透系数和相对水深条件下波高的衰减规律,指出衰减速率随着海床渗透系数的增大和相对水深的减小而变大[7]。上述研究成果有助于认识各类渗透海床上的波高变化规律,但鲜有关于波浪在渗透海床上传播波长变化的研究报道。因此,本文基于线性波浪理论,研究沙质海床上的波长变化规律,探求引起波长变化的物理机制。
1 数学模型和理论基础针对波浪在无限厚沙质海床上沿x轴正方向传播的二维运动问题,根据Dean和Dalrymple的推导结果[4],速度势可表示为:
| $\varphi \left( {x,z} \right) = - \frac{{{\rm{i}}Ag}}{{\omega \left( {1 - {\rm{i}}\omega T{\rm{tanh}}\left( {kh} \right)} \right)}}\frac{{{\rm{cosh}}\left( {z + h} \right) - {\rm{i}}\omega T{\rm{sinh}}k\left( {z + h} \right)}}{{{\rm{cosh}}\left( {kh} \right)}}{\rm{exp}}({\rm{i}}kx)$ | (1) |
式中:
相应地,色散关系(方程)为:
| ${\omega ^2}\left( {1 - {\rm{i}}\omega T{\rm{tanh}}kh} \right) = gk\left( {{\rm{tanh}}kh - {\rm{i}}\omega T} \right)$ | (2) |
为了研究波浪在沙质海床上传播时波长的变化规律,需要在已知水深、波浪周期和沙质海床渗透系数的条件下,求解色散方程式(2) 中的复波数k。参考Mendez提出的摄动解法[8],该方法假设渗透系数的轻微扰动会引起波数的微小变化,计算步骤如下:
(1) 对色散方程式(2) 进行无量纲化处理,得
| $\lambda - x{\rm{tanh}}x = \psi \left( {\lambda {\rm{tanh}}x - x} \right)$ | (3) |
式中:λ=ω2h/g;x=kh;ψ=iωT。
(2) 令ψ=0,则式(3) 可以简化为:
| $\lambda = {x_{|\psi = 0}}{\rm{tanh}}{x_{|\psi = 0}}$ | (4) |
此即为海床不可渗透条件下无量纲化后的色散方程。采用迭代方法,便可得xψ=0=x0,作为求解式(3) 中x的初值。
(3) 定义δψ=ψ/N为小变量,则ψi=ψi-1+δψ,i=1, 2, …, N。其中,N为区间数,ψ0=0。
(4) 按照式(5) 计算δxi,则xi=xi-1+δxi,i=1, 2, …, N。
| $\delta {x_i} = \delta \psi \frac{{\lambda {\rm{tanh}}{x_{i - 1}} - {x_{i - 1}}}}{{{\psi _{i - 1}} - {\rm{tanh}}{x_{i - 1}} - \frac{{{x_{i - 1}} + \lambda {\psi _{i - 1}}}}{{{\rm{cos}}{{\rm{h}}^2}{\psi _{i - 1}}}}}}$ | (5) |
(5) 重复步骤(3) 和(4),直至ψ=ψN=ψN-1+δψ,此时x=xN=xN-1+δxN即为式(3) 的复数根,则复波数k=x/h。
2 计算结果与分析针对开敞平直的沙质海岸,海床坡度相对较小,通常介于1:50~1:500[9],且等深线近似相互平行,因此可应用第1节中的数学模型来研究波浪在沙质海床上传播时不同渗透系数和相对水深对波长的影响规律,进而探求影响波长的物理机制。
2.1 渗透系数对波长变化的影响沙质海床渗透性是引起波长变化的直接原因。试验结果表明,不同类型沙质海床的渗透系数Ks约为10-2~10-4 m/s[10-11]。设水深h=5 m,波浪周期分别取3和5 s(实际观测波浪平均周期一般为3~5 s),对应的波浪圆频率分为ω1=2.094 4 Hz和ω2=1.256 6 Hz,利用给出的色散方程求解方法,在确定合适区间数N的前提下,可求得波长L和空间衰减系数ki。如表 1所示,通过与文献[7]中迭代法计算结果的对比,可以发现,采用Mendez提出的计算方法求得的复波数k,其实部kr在区间数N较小的情况下,就可达到较高的计算精度,而虚部ki的收敛速度则随着区间数N的增大表现为先快后慢。因此,为了得到高精度计算结果,取区间数N=200。
| 表 1 不同区间数时计算结果的相对误差 Table 1 Relative calculation errors with different interval number N |
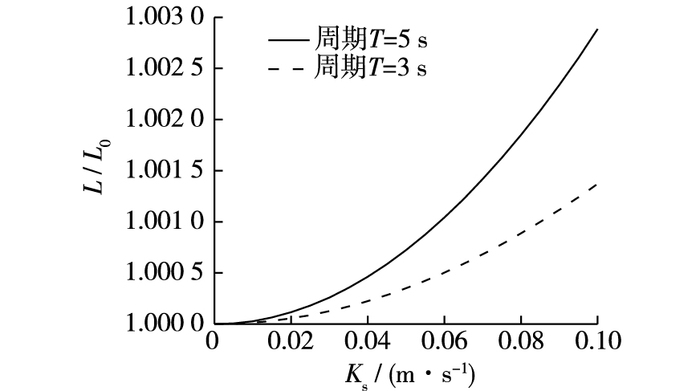
图 1是相对波长L/L0随渗透系数Ks的变化规律,其中L0为Ks=0时计算得到的波长,在本算例中分别等于13.75和30.29 m。可以看出,随着海床渗透系数的变大,相对波长也略有增加,这说明在水深和波浪周期一定的条件下,波浪在沙质海床上传播时的波长略大于海底不可渗透时的情况,且组成沙质海床的泥沙颗粒越大,即渗透系数越大,波长的增大也越大。
|
图 1 相对波长L/L0随渗透系数的变化 Figure 1 Changes of wavelength ratio L/L0 versus permeability coefficients |
相对水深可以反映沙质海床对波浪的影响程度。设沙质海床上深水入射波的波长为LI,随着波浪的向岸传播,水深h处的波长为L,而同等水深h、海底不可渗透(即Ks=0) 条件下对应的波长为L0。相对波长L/LI随相对水深h/L的变化见图 2。可见沙质海床上的波浪,在由深海向近岸传播过程中,波长逐渐减小,这是波浪浅水变形的结果,是引起波长变化的主要原因。从不同类型沙质海床上的波长与不可渗透海床上波长的比值L/L0随相对水深h/L的变化(图 2)可见,随着水深减小,渗透海床上的波长与不可渗透海床上的波长相比越来越大。这说明,受海底渗透的影响,波浪因浅水变形引起的波长减小在数值上略小于海床不可渗透的情况,且这种差别随着相对水深的减小而增大。

|
图 2 相对波长L/L0和L/LI随相对水深的变化 Figure 2 Changes of wavelength ratio L/L0and L/LI versus non-dimensional wave depth h/L |
综上所述,波浪在沙质海床上传播时,受海底渗透的影响,波长略大于海底不可渗透的情况,且这种影响随着海床渗透系数的增大或相对水深的减小而变大。可以认为,由于水质点会通过沙质海床的孔隙渗流进入海床内部[12],因此,沙质海床的渗透性对波长的影响相当于存在一个“海床水深”Δh,即当波浪在水深为h的沙质海床上传播时,其波长在数值上等于波浪在水深为h+Δh的不可渗透海床上传播的情况,Δh=ΔhKs, h/L是关于海床渗透系数和相对水深的函数,并随着Ks的增大和h/L的减小而增大。这就解释了在水深和波浪周期一定的条件下,沙质海床上的波长相对较大原因。
3 结语(1) 在已知波浪周期、海床渗透系数和水深的条件下,采用Mendez提出的方法求解复波数,其实部在区间数N较小的情况就可以达到较高的计算精度,而虚部的收敛速度则随着区间数N的增大表现为先快后慢。
(2) 沙质海床是由不同大小的泥沙颗粒组成的多孔介质,具有渗透性。波浪在沙质海床上传播时,其波长略大于同等水深不可渗透海床上的波长,且随渗透系数的增大而增大。
(3) 沙质海床上的波浪在向岸传播过程中会发生浅水变形而波长减小,但相比海床不可渗透的情况,波长的减小程度相对较小,且随着相对水深的变小,这种现象更加明显。
(4) 沙质海床的渗透性对波长的影响可等效于一个“海床水深”Δh,它随渗透系数Ks的增大和相对水深h/L的减小而增大。当波浪在水深为h的沙质海床上传播时,其波长在数值上等于水深为h+Δh的不可渗透海床上的波长。
| [1] |
PUTNAM J A. Loss of wave energy due to percolation in a permeable sea bottom[J]. Eos, Transactions American Geophysical Union, 1949, 30(3): 349-356. DOI:10.1029/TR030i003p00349 |
| [2] |
SAVAGE R P, FAIRCHILD J C. Laboratory study of energy losses by bottom friction and percolation[Z]. Beach Erosion Board, Corps of Engineers, Technical Memorandum, No.31, 1953.
|
| [3] |
SAWARAGI T, DEGUCHI I. Waves on permeable layers[C]//Proc 23rd Coast Eng Conf, Venice, 1992: 1531-1544.
|
| [4] |
DEAN R G, DALRYMPLE R A. Water wave mechanics for engineers and scientists[M]. New Jersey: Prentice Hall Inc, 1984.
|
| [5] |
SILVA R, SALLES P, PALACIO A. Linear waves propagating over a rapidly varying finite porous bed[J]. Coastal Engineering, 2002, 44(3): 239-260. DOI:10.1016/S0378-3839(01)00035-7 |
| [6] |
刘忠波, 孙昭晨, 房克照. 波浪在渗透海床上传播的数学模型及其验证[J]. 大连理工大学学报, 2013, 53(3): 417-422. ( LIU Zhongbo, SUN Zhaochen, FANG Kezhao. Mathematical model for wave propagation over a porous seabed and its numerical validation[J]. Journal of Dalian University of Technology, 2013, 53(3): 417-422. DOI:10.7511/dllgxb201303017 (in Chinese)) |
| [7] |
唐志波, 倪云林, 于姜梅, 等. 渗透海床上波浪传播特性的研究[J]. 船舶力学, 2016, 20(1): 77-82. ( TANG Zhibo, NI Yunlin, YU Jiangmei, et al. Research of the characteristics of wave propagation over porous bottom[J]. Journal of Ship Mechanics, 2016, 20(1): 77-82. (in Chinese)) |
| [8] |
MENDEZ F J, LOSADA I J. A perturbation method to solve dispersion equations for water waves over dissipative media[J]. Coastal Engineering, 2004, 51(1): 81-89. DOI:10.1016/j.coastaleng.2003.12.007 |
| [9] |
邹志利, 房克照. 海岸动力地貌[M]. 大连: 大连理工大学, 2014: 93-94. ( ZOU Zhili, FANG Kezhao. Coastal dynamic geomorphology[M]. Dalian: Dalian University of Technology, 2014: 93-94. (in Chinese))
|
| [10] |
于通顺, 王海军. 循环荷载下复合筒型基础地基孔隙水压力变化及液化分析[J]. 岩土力学, 2014, 35(3): 820-826. ( YU Tongshun, WANG Haijun. Pore water pressure fluctuation and liquefaction analysis of subgrade for composite bucket foundation under cyclic loading[J]. Rock and Soil Mechanics, 2014, 35(3): 820-826. (in Chinese)) |
| [11] |
程永舟. 波浪与多孔介质相互作用的水动力特征研究[D]. 大连: 大连理工大学, 2008 (CHENG Yongzhou. Hydrodynamic behaviors of waves interaction with porous medium[D]. Dalian: Dalian University of Technology, 2008. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10141-2007211018.htm
|
| [12] |
王忠涛, 栾茂田, 郑东生. 多孔介质海床对波浪传播影响理论分析[J]. 大连理工大学学报, 2009, 49(6): 891-896. ( WANG Zhongtao, LUAN Maotian, ZHENG Dongsheng. Dynamic analysis for effects of porous seabed on wave propagation[J]. Journal of Dalian University of Technology, 2009, 49(6): 891-896. DOI:10.7511/dllgxb200906020 (in Chinese)) |
2. State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China
 2017
2017 
