2. 河北省水利水电第二勘测设计研究院,河北石家庄 050021
受人类活动影响,如城市下垫面不透水面积增加、城市向低洼易涝区扩张、城市热岛效应与雨岛效应等,城市内涝灾害越来越频繁[1]。我国当前正处在城市化快速发展阶段,城市化水平将不断提高,与之不相符的是城市防洪排涝标准普遍偏低,城市洪涝灾害损失持续增长[2]。因此,数值模拟城市暴雨内涝的形成及演进过程,开展城市暴雨内涝积水的风险分析,为防涝救灾和城市发展规划提供决策依据,显得尤为重要。
为了更精确计算城市暴雨内涝的淹没深度和范围,二维水动力学模型越来越广泛引用到城市洪涝数值模拟计算中。水动力模型计算获得任意时刻的流速、流向和水深,能够更真实、更全面、更立体地体现城市复杂环境下的水流现象。近年来,仇劲卫等[3]采用无结构不规则网格,以二维非恒定水力模型为基础,模拟了天津市暴雨沥涝过程;解以扬等[4-5]针对特定的研究区域对该模型进行了改进,验证结果表明改进模型对南京、南昌及上海等城市也具有良好适用性。Norton等[6]采用有限元算法求解了水深平均的二维水动力学模型;何文华[7]基于无结构网格的水动力模型对济南市二环路以内区域马路行洪和地表积水进行了数值模拟;黄清雨等[8]采用地理信息系统技术(GIS)与水文/水动力学相结合的方法,利用局部等体积法和水动力模型模拟了上海中心城区的暴雨内涝;喻海军[9]基于非结构网格中心型的有限体积法,采用Godunov型格式计算界面通量,并将分片线性逼近的MUSCL格式应用于变量重构,建立了时空均具有二阶精度的二维水动力学模型,同时引入隐式的双时间步算法以提高二维模型的稳定性和计算效率,并将模型应用于广州新河浦社区暴雨洪水计算。城市暴雨内涝二维水动力模拟的精度与基础地形数据精度直接相关联,且城区内排水系统(如管网、泵站)以及房屋建筑、城市道路等城市典型地物均为雨水汇流过程的主要影响要素,直接影响涝水的演进过程。目前,综合考虑多种因素的城市暴雨内涝精细化水动力模型研究却少见报道。
本文基于石家庄市高精度地形数据,采用DHI公司开发的MIKE软件,利用小尺寸结构化网格建立城市暴雨内涝精细化水动力模型。模型充分考虑城区内不同的土地利用类型,赋予房屋建筑一定高度,体现各片街区雨水管道及立交泵站排水能力。
1 模型原理暴雨内涝模型为二维水动力模型,模型控制方程是基于Navier-Stokes方程沿水深平均的平面二维浅水方程。基于结构化矩形网格采用有限差分方法对控制方程进行离散与求解,采用隐式交替格式(ADI)[10]可防止离散过程中可能发生的质量、动量和能量失真,Taylor级数展开的截断误差可达二阶至三阶精度,计算结果精确;与显式格式相比,可取较大时间步长,计算效率较有限体积法高。同时针对城市典型地物特点以及复杂水流环境,采取系列精细化措施进一步提高模型精度。
1.1 基本方程二维水动力模型平面二维浅水控制方程包括连续性方程和动量方程,
| $ \partial \zeta /\partial t + \partial p/\partial x + \partial q/\partial y = \partial d/\partial t $ | (1) |
| $ \frac{{\partial p}}{{\partial t}} + \frac{\partial }{{\partial x}}\left( {\frac{{{p^2}}}{h}} \right) + \frac{\partial }{{\partial y}}\left( {\frac{{pq}}{h}} \right) + gh\frac{{\partial \zeta }}{{\partial x}} + \frac{{gp\sqrt {{p^2} + {q^2}} }}{{{C^2}{h^2}}} - \\ \frac{1}{{{\rho _{\rm{w}}}}}\left[ {\frac{\partial }{{\partial x}}\left( {h{\tau _{xx}}} \right) + \frac{\partial }{{\partial y}}\left( {h{\tau _{xy}}} \right)} \right] - {\mathit{\Omega }_q} - fV{V_x} + \frac{h}{{{\rho _{\rm{w}}}}}\frac{\partial }{{\partial x}}\left( {{p_{\rm{a}}}} \right) = 0 $ | (2) |
| $ \frac{{\partial q}}{{\partial t}} + \frac{\partial }{{\partial x}}\left( {\frac{{pq}}{h}} \right) + \frac{\partial }{{\partial y}}\left( {\frac{{{q^2}}}{h}} \right) + gh\frac{{\partial \zeta }}{{\partial y}} + \frac{{gq\sqrt {{p^2} + {q^2}} }}{{{C^2}{h^2}}} - \\ \frac{1}{{{\rho _{\rm{w}}}}}\left[ {\frac{\partial }{{\partial x}}\left( {h{\tau _{xy}}} \right) + \frac{\partial }{{\partial y}}\left( {h{\tau _{xy}}} \right)} \right] + {\mathit{\Omega }_p} - fV{V_y} + \frac{h}{{{\rho _{\rm{w}}}}}\frac{\partial }{{\partial y}}\left( {{p_{\rm{a}}}} \right) = 0 $ | (3) |
式中:h为总水头,h=d+ζ(d为静水深,ζ为控制体水位); p,q分别为x和y方向的单宽流量; g为重力加速度; C为谢才系数; Ω为科氏力系数; f为阻力系数; ρw为水密度; V为风速; Vx,Vy为风速在x,y方向的分量;Pa为大气压。
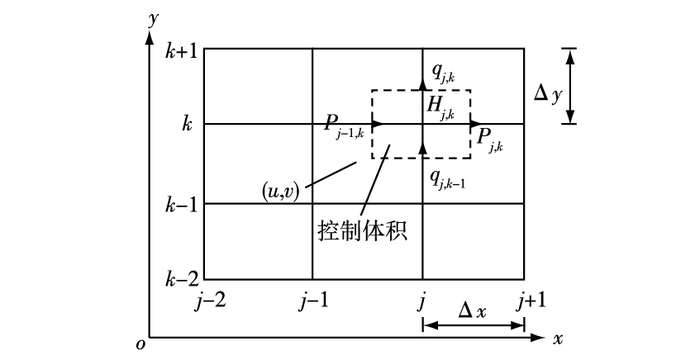
1.2 方程的离散采用隐式交替方向(ADI)离散模型连续方程和动量方程[11-12],各重要系数和微分项均采用中心差分格式。模型网格布置见图 1。
|
图 1 模型网格布置 Figure 1 Model grid layout |
X,Y方向连续方程可表示为:
| $ \begin{array}{*{20}{c}} {2{{\left( {\frac{{{\zeta ^{n + 1/2}} - {\zeta ^n}}}{{\Delta t}}} \right)}_{j,k}} + \frac{1}{2}{{\left\{ {\left( {\frac{{{p_j} - {p_{j - 1}}}}{{\Delta x}}} \right) + {{\left( {\frac{{{p_j} - {p_{j - 1}}}}{{\Delta x}}} \right)}^n}} \right\}}_k} + }\\ {\frac{1}{2}{{\left\{ {\left( {\frac{{{q_k} - {q_{k - 1}}}}{{\Delta y}}} \right) + {{\left( {\frac{{{q_k} - {q_{k - 1}}}}{{\Delta y}}} \right)}^{n - 1/2}}} \right\}}_j} = 2{{\left( {\frac{{{d^{n + 1/2}} - {d^n}}}{{\Delta t}}} \right)}_{j,k}}} \end{array} $ | (4) |
| $ \begin{array}{*{20}{c}} {2{{\left( {\frac{{{\zeta ^{n + 1}} - {\zeta ^{n + 1/2}}}}{{\Delta t}}} \right)}_{j,k}} + \frac{1}{2}{{\left\{ {\left( {\frac{{{p_j} - {p_{j - 1}}}}{{\Delta x}}} \right) + {{\left( {\frac{{{p_j} - {p_{j - 1}}}}{{\Delta x}}} \right)}^n}} \right\}}_k} + \frac{1}{2}{{\left\{ {{{\left( {\frac{{{q_k} - {q_{k - 1}}}}{{\Delta y}}} \right)}^{n + 3/2}} + {{\left( {\frac{{{q_k} - {q_{k - 1}}}}{{\Delta y}}} \right)}^{n + 1/2}}} \right\}}_j} = }\\ {2{{\left( {\frac{{{d^{n + 1}} - {d^{n + 1/2}}}}{{\Delta t}}} \right)}_{j,k}}} \end{array} $ | (5) |
对动量方程逐项给出离散格式,此处仅给出x方向动量方程格式,y方向动量方程离散格式类似。
时间偏导项,可表示为:
| $ \frac{{\partial p}}{{\partial t}} \approx {\left( {\frac{{{p^{n + 1}} - {p^n}}}{{\Delta t}}} \right)_{j,k}} $ | (6) |
重力项,可表示为:
| $ gh{\zeta _x} \approx g{\left( {\frac{{{h_{j,k}} + {h_{j + 1,k}}}}{2}} \right)^n}{\left( {\frac{{{\zeta _{j + 1,k}} + {\zeta _{j,k}}}}{{\Delta x}}} \right)^{n + 1/2}} $ | (7) |
对流项,可分别表示为:
| $ \frac{\partial }{{\partial x}}\left( {\frac{{pp}}{h}} \right) \approx {\left[ {\frac{{{{\left( {{p_{j + 1}} + {p_j}} \right)}^{n + 1}}}}{2}\frac{{{{\left( {{p_{j + 1}} + {p_j}} \right)}^n}}}{2}\frac{1}{{h_{j + 1}^n}} - \frac{{{{\left( {{p_j} + {p_{j - 1}}} \right)}^{n + 1}}}}{2}\frac{{{{\left( {{p_j} + {p_{j - 1}}} \right)}^n}}}{2}\frac{1}{{h_j^n}}} \right]_k}\frac{1}{{\Delta x}} $ | (8) |
| $ \frac{\partial }{{\partial y}}\left( {\frac{{pq}}{h}} \right) \approx \left[ {\left( {\frac{{p_{k + 1}^a + p_k^b}}{2}} \right)v_{j + 1/2,k}^{n + 1/2} - \left( {\frac{{p_k^a + p_{k - 1}^b}}{2}} \right)v_{j + 1/2,k - 1}^{n + 1/2}} \right]\frac{1}{{\Delta y}} $ | (9) |
其中,向下追赶时,a=n+1, b=n;向上追赶时a=n, b=n+1,表达式可写成:
| $ v_{j + 1/2,k - 1}^{n + 1/2} = 2\left( {{q_j} + {q_{j + 1}}} \right)_k^{n + 1/2}/\left( {{h_{j,k}} + {h_{j,k + 1}} + {h_{j + 1,k}} + {h_{j + 1,k + 1}}} \right) $ | (10) |
| $ v_{j + 1/2,k}^{n + 1/2} = 2\left( {{q_j} + {q_{j + 1}}} \right)_{k - 1}^{n + 1/2}/{\left( {{h_{j,k - 1}} + {h_{j,k}} + {h_{j + 1,k - 1}} + {h_{j + 1,k}}} \right)^n} $ | (11) |
底床阻力项,可表示为:
| $ gp\sqrt {{p^2} + {q^2}} /\left( {{C^2}{H^2}} \right) = gp_{j,k}^{n + 1}\sqrt {{p^{ * 2}} + {q^{ * 2}}} /\left( {{C^2}{H^{ * 2}}} \right) $ | (12) |
| $ {p^ * } = p_{j,k}^n $ | (13) |
| $ {q^ * } = \left( {q_{j,k}^{n - 1/2} + q_{j + 1,k}^{n - 1/2} + q_{j,k - 1}^{n - 1/2} + q_{j + 1,k - 1}^{n - 1/2} + q_{j,k}^{n + 1/2} + q_{j,k - 1}^{n + 1/2} + q_{j + 1,k - 1}^{n + 1/2}} \right)/8 $ | (14) |
| $ {H^ * } = \left\{ \begin{array}{l} H_{j,k}^n,\;\;\;\;\;\;\;{p^ * } \ge 0\\ H_{j - 1,k}^n,\;\;\;\;\;{p^ * } < 0 \end{array} \right. $ | (15) |
采用有限差分法求解方程,包括空间差分和时间中心差分[12]。
(1) 空间差分法。采用ADI逐行法对连续及动量方程分别进行时空上的积分,每个方向及每个单独网格线产生的方程矩阵用追赶法求解。
(2) 时间中心差分法。将1个时间步长中心差分分为x-sweep(t从n到n+1/2) 和y-sweep(t从n+1/2到n+1)。方程采用一维推进方式,x-sweep方向求解x连续方程和x动量方程时,ζ从n到n+1/2,p从n到n+1,q为已知的n-1/2到n+1/2的值;y-sweep方向求解y连续方程和y动量方程时,ζ从n到n+1/2,q从n到n+1, p为已知的n-1/2到n+1/2的值。
时间中心差分形式在x-sweep后立刻进行y-sweep的循环求解,由于动量方程中的交叉项求解很难找到一个合适的时间中心点,因此采用side-feedind差分方式对动量方程中的交叉项求导。
1.4 精细化措施(1) 小尺寸网格剖分。在高精度地形数据的基础上,取较小的网格剖分尺度,真实体现城区内典型地物及复杂地形,并很好地反映水流边界。
(2) 城区建筑物概化。赋予房屋建筑一定实体高度,实现屋面雨水下排和建筑实体阻水效果。
(3) 糙率分区与径流分区。城市核心城区大部分土地为建设用地,地面高度硬化;新建城区和城郊结合部的建筑密度较老城区小,土地利用中绿地和农田占比较大;城区用地类型包括居民建筑、硬质地面、交通道路、排水明渠及绿地等,模型针对各类用地选取不同径流系数和糙率。
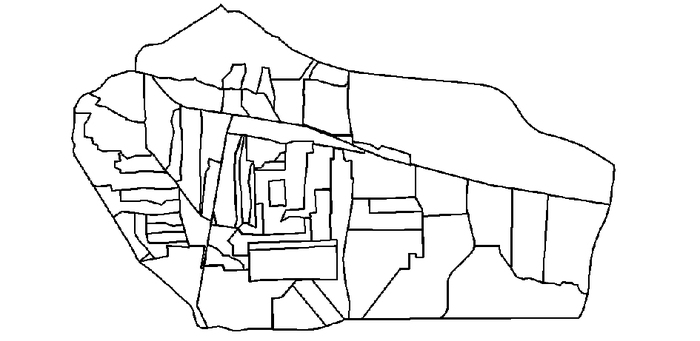
(4) 排水分区精细划分。以石家庄市为例,考虑地形地势、河渠水系、城市建设时序等因素,石家庄市主城区现状排水系统共划分为五支渠、桥西明渠、元村明渠、南栗明渠、石津南支渠、东明渠、总退水渠、滹沱河、东南环水系(包括环山湖)、汪洋沟、良村东部等11个排水分区,如图 2所示。在以上排水分区基础上,根据主干管分布位置、集水区域等情况,将排水分区精细划分至各雨水干管实际控制街区,最终得到55个子排水分区,如图 3所示。细化分区能更有效地模拟城市管网排水的实际过程,地面汇流过程也更贴合具体情景。

|
图 2 雨水排放系统排水分区 Figure 2 Partition schematic of drainage system |
|
图 3 雨水排放系统细化后排水分区 Figure 3 Refined partition schematic of drainage system |
(5) 源汇设置。源点是外部水进入模型,汇点是水从模型流出进入外部。以源点模拟排水管口,以汇点模拟城市泵站。
(6) 干湿水深设定[13]。设定网格干湿水深值,当网格单元的水深小于干水深时网格单元不作为水域参与控制方程的计算;当该单元格水深介于干湿水深之间时,该单元格只计算质量通量;网格单元水深大于湿水深时,同时计算质量通量和动量通量。干湿网格方法提高了模型计算效率和稳定性,同时,针对城市暴雨模拟设定的干湿水深值很小,可以模拟暴雨积水后的流动。
2 模型建立城市暴雨内涝水动力模型通过采取系列精细化处理措施,还原了真实城区地形,较全面地反映了城市各类典型地物,对石家庄市主城区进行暴雨内涝模拟,并结合淹没结果进行风险分析。
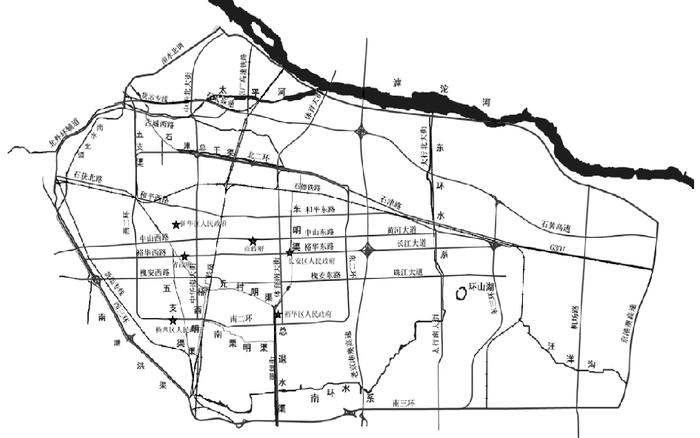
2.1 模拟区域概况主城区总面积520.08 km2,研究范围西部和南部以三环路为界,西北部以防洪堤结合南水北调工程为界,北部以滹沱河右堤为界,东部包括高新开发区,以新建京港澳高速为界,包括石家庄市新华区、桥西区、桥东区、裕华区、长安区和藁城区及栾城区的局部。石家庄地势整体呈西北高、东南低,主要道路包括京广铁路、石太铁路、石德铁路、货运专线、107国道、307国道、石黄高速、石太高速、原京港澳高速等,主要河渠水系有五支渠、元村明渠、南栗明渠、东明渠、总退水渠等,如图 4所示。近些年,该市极端天气逐渐增多,陆续发生局部短历时强降雨,因暴雨强度超出排水管网及泵站排水能力,造成城区大范围积水,损失严重。
|
图 4 石家庄市主城区主要道路和水系分布 Figure 4 Main roads and water system in Shijiazhuang |
主城区地物较为复杂,包括建筑、硬质地面、道路、排水明渠及绿地等。建筑及硬质地面属不透水区域,道路为主要行涝通道,排水明渠是城市排水的主要通道。综合考虑建筑、道路及计算时间等因素,采用20 m×20 m的矩形结构化网格剖分研究区域,共剖分219.23万个网格。
2.2.2 内边界确定内边界主要包括堤防、道路等阻水建筑物以及桥梁、涵洞、闸等过水建筑物。1:1 000地形图高程点分布密集,且区域网格划分尺寸足够小,生成的地形文件能够有效反映各地物实际高程。当水位达到阻水建筑物顶部高程时,以漫溢形式通过;而线状构筑物沿程桥梁、涵洞,允许涝水正常演进,其中规模较大的线状构筑物有京广铁路、石德铁路、石黄高速、石太高速、京港澳高速等。
城市的建筑房屋,从降雨和汇流角度考虑,屋顶雨水排出迅速,且具有不透水的特性;从行涝角度考虑,房屋实体具有阻水作用。因此,计算中整体拔高建筑房屋所在的网格高程,拔高尺度为4 m。屋顶汇流为雨水自高地向低处汇集,由模型基本方程控制。
石家庄市主城区共有43座雨水排水泵站,包括集中在地道桥及下穿式立交桥处的39座一般性泵站,4座区域性排水泵站。该市泵站的抽水管口均设在地道桥下和下穿式立交桥下最低点,依据地形图确定泵站服务区,设定积水区最低点网格为泵站位置,以汇点形式体现泵站排水功能。
研究区域共有排水出口110处,包括方涵出口70处,圆管出口40处(其中管径小于800 mm未计)。依据排水出口点位置确定排水出口附近水域,选取距离出口最近水域网格作为排水出口位置,以源点形式体现排水出口的雨水出流。
2.2.3 抽排水能力确定城市排水管网涝水收纳能力与其所在排水分区系统的管网排水能力直接相关。考虑管网排水能力时,以净雨量折算的形式等效处理,净雨折算量与所在排水分区的排水能力相对应。即通过统计各细化排水分区排水出口总设计流量,除以所在排水分区面积作为该区管网排水能力。通过在细化的子排水分区上叠加各自对应的净雨折算过程,得到随时间和空间变化的排水文件,作为模型排水边界条件。
依据排水泵站实际调度规则,考虑将泵站所在积水区涝水强排入相应排水管网。管道水量(净雨折算量和泵站强排水量)由出水口排放至对应排水渠道,考虑出水口的排水能力与设计能力相一致。
在强降雨过程中,城市排水渠道水位先涨后落,雨峰后渠道下游段部分排水管道出口被淹没,对管网排水产生顶托。考虑以顶托系数体现渠道顶托影响。比较管道出口高程和相应位置水位过程确定顶托时段;结合顶托水位和管道参数确定受顶托影响的管道长度和顶托系数,进而调整对应子排水分区的排水过程。
2.2.4 径流与糙率确定石家庄市主城区建设用地包括建筑房屋、硬质地面、广场花园等各种类型,对于坡面屋顶,降雨湿润屋面后便直接形成径流下落至地面;对于平面屋顶,大多设有畅通的导流管道,依据《室外排水设计规范(2014版)》,一般建筑屋顶的径流系数为0.9[14];对于硬质地面,除具有不透水性的混凝土地面之外,还包括干砌石地面、砖石地面等,广场地砖通常具有一定下渗能力,花园和小区的绿化区域能够吸收大部分雨水,综合考虑以上因素,确定建筑用地径流系数统一取值为0.80。
参考倪丽丽等[15]基于石家庄局部城区的城市暴雨内涝模型中径流系数取值,公园绿地为0.15,裸地为0.3,城市道路为0.85,本研究中道路含两侧人行道及绿化带,故道路径流系数取为0.70。各类用地径流系数如表 1所示。
| 表 1 分区径流系数和分区糙率系数 Table 1 Partitioned runoff coefficients and roughness |
根据《城市防洪工程设计规范》,城市商业区糙率为0.015~0.030,密集住宅区糙率为0.025~0.040。城区建筑物形成的封闭场院和纵横交错的街巷延长了汇流路径,致使核心城区尤其是房屋建筑、庭院密集区域的糙率比一般建设用地大。综合楼房房顶、硬质地面、广场花园等细分土地类型的糙率,确定建设用地糙率系数取值为0.035。各类用地糙率如表 1所示。
2.2.5 干湿边界及计算步长确定影响城市暴雨内涝水动力模型运行稳定性和效率的主要参数包括干、湿水深以及计算步长。根据网格质量、内涝情况及区域地形复杂程度,设定计算区域网格为干单元,设网格干水深0.02 m,湿水深0.03 m,时间步长为1.5 s,输出时间步长为10 min。
2.3 模型验证据记载,石家庄市历史上发生严重涝灾的年份有1963年和1996年。为说明模型合理性,对模型进行验证,下面以“96.8”降雨为例,从计算过程的流场、流态、淹没情况及与历史上易积水点对比等方面分析,验证计算模型的合理性与可靠性。
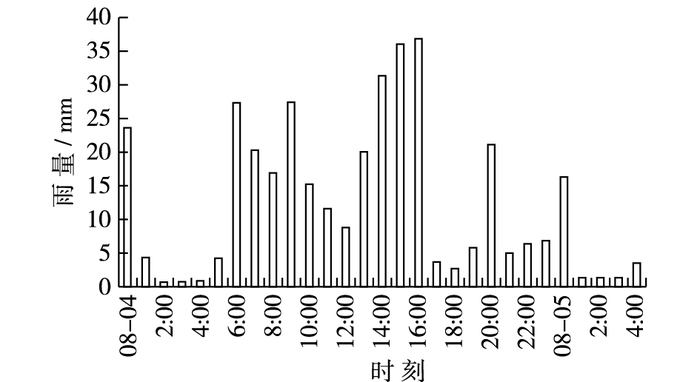
石家庄站1996年实测降雨过程见图 5。根据石家庄站“96.8”实测暴雨资料,以8月3日23时作为模拟起始时间,8月5日4时作为模拟终止时间,计算“96.8”降雨过程和积涝过程,模型计算时间步长1.5 s,输出时间间隔为10 min。
|
图 5 “96.8”石家庄站实测降雨过程 Figure 5 "96.8" rainfall at Shijiazhuang station |
根据“96.8”暴雨内涝模型计算结果,统计研究范围内地道桥、下穿路和立交桥的最大积水深度。统计数据显示,“96.8”暴雨条件下主城区淹没水深超过1 m的地道桥和立交桥共22处,其中地道桥21处,立交桥1处;胜利北大街地道桥最大积水深为5.03 m。根据“96.8”暴雨内涝资料记录,市区内20座地道桥大部分因积水交通中断,胜利北大街地道桥下局部区域积水深达5 m,其他另有积水断交路段35处。通过模型计算结果和历史信息资料比较验证分析,地道桥淹没情况基本吻合,说明所建暴雨内涝精细化计算模型基本合理。
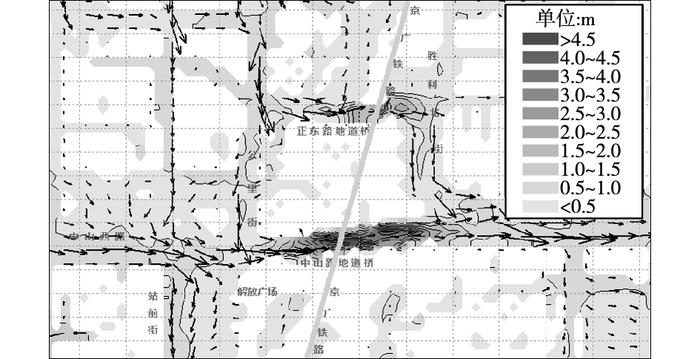
根据“96.8”暴雨内涝资料记录,中山路地道桥因地势低洼,降雨开始后附近涝水迅速向该处汇集,水深和流速均较大,造成中山路地道桥挡墙严重断裂。中山路地道桥及其附近区域流场分布,如图 6所示。“96.8”降雨模拟结果显示:地道桥内积水深度超过4.5 m,且水流湍急,对挡墙产生持续冲击作用,由此说明了以地道桥为代表的重点积水区流场及流态的合理性,进一步验证了模型的精细化及合理可靠性。
|
图 6 “96.8”降雨中山路地道桥及其附近区域流场分布 Figure 6 Flow field in Zhongshan Road underpass bridge and vicinity in "96.8" |
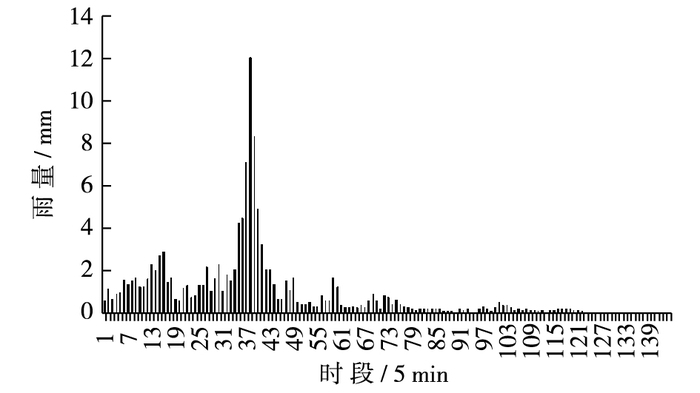
基于已验证的石家庄市主城区暴雨内涝精细化水动力模型,研究100年一遇12 h降雨条件下,该市主城区涝水形成及淹没情况,并对降雨情景进行风险分析,暴雨过程如图 7所示。
|
图 7 100年一遇设计12 h暴雨过程线 Figure 7 12 h rainstorm hydrograph of 100-year return period design flood |
城市内具有一系列典型地物,这些地物使得涝水在发展过程中形成了具有城市典型流场特征的淹没区。裕华西路与中华南大街立交桥附近积水路段的流场分布如图 8所示,可以看出,立交桥下形成积水点并发展成为大的积水区域;中华南大街、裕华西路、站前街、南长街等道路作为行涝通道影响着涝水的演进;涝水遇到房屋建筑受到阻碍并绕行;在宽度较小的街巷如站前街处形成较深积水,且街巷两端流场呈扩散状;房屋建筑群的围绕和机关单位的围墙形成了大量的庭院,暴雨在庭院中汇集后形成较深积水,这部分涝水不能像坡面汇流一样顺地势沿最短路径流动,只能通过庭院的口门向外流出。

|
图 8 裕华西路中华南大街立交桥附近积水路段流场分布 Figure 8 Flow field in Yuhua Road and Zhonghua Street overpass and vicinity |
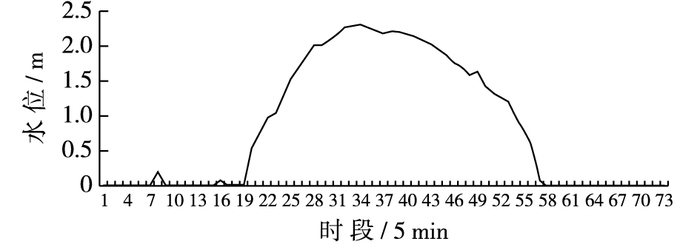
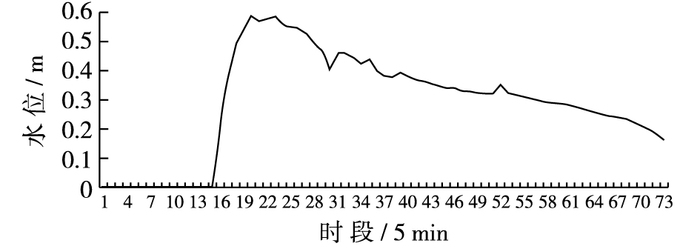
城市泵站多位于易积水的地道桥、下穿路和立交系统附近,用以排出涝区积水。下面以100年一遇12 h降雨条件下,南二环与胜利南街立交桥和工人街地道桥的水深过程线为例,分析泵站的抽排水作用和积水点的涨退水过程,如图 9和10所示。降雨开始时,四面汇集来的雨水首先通过位于较低位置的雨篦口进入汇水池,再由泵站将积水抽排出去。在这个过程中,由于降雨初始水量较小、排水能力相对较大,地面没有形成积水。随着降雨历时的增加、降雨量增大和雨峰的到来,泵站未能及时排出四面汇来的雨水,开始形成积水区域,积水水位迅速升高,将导致较长时间的交通中断现象。降雨临近结束,降雨量大大减少,泵站仍持续工作,可基本排出降雨后期产生的积聚涝水,恢复积水点处的正常交通。
|
图 9 南二环与胜利南街立交桥水深变化过程 Figure 9 Water depth hydrograph under South Second Ring Road and Shengli Street overpass |
|
图 10 工人街地道桥水深变化过程 Figure 10 Water depth hydrograph under Workers Street underpass bridge |
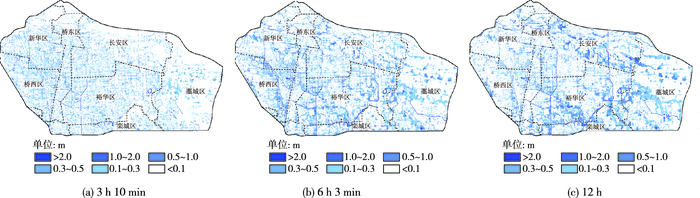
石家庄市主城区100年一遇12 h降雨条件下,不同时段淹没水深分布见图 11。
|
图 11 不同时段淹没水深分布 Figure 11 Distribution of waterdepth at different time |
分析图 11可见,降雨开始后3 h10 min达到雨峰,雨峰历时1 h,峰内降雨71.36 mm,与主峰前降雨量总和相当,计算区内积水面积迅速扩大,大部分积水区积水深度大于0.1 m;积水深度在0.3 m以上的积水点和积水路段明显增多,且多集中在元村明渠北侧桥东区中部区域、元村明渠西北侧桥西区东北部区域、元村明渠和南栗明渠之间的裕华区中西部区域以及太平河沿岸一带;大量出现1 m以上的深积水危险区域,联盟路下穿京广高速铁路低洼区域水深2~4 m,胜利北街下穿石太铁路最低点水深4.46 m,且各深积水点附近均有较长的积水路段,这些路段已不具备机动车通行条件,部分路段交通已基本陷入瘫痪状态。降雨开始后12 h,最后6 h内降雨量仅为26.85 mm,雨量减少和管网持续排水使得地面积水险情有所缓和,除部分地势低洼的积水点仍有积水之外,核心城区内大部分区域地面积水已经基本排除,积水严重路段积水深度已退至0.3 m以下,基本不影响机动车通行。
经统计分析,100年一遇12 h降雨条件下,积水深超过0.3 m而发生交通中断路况的地道桥、下穿路和立交系统共35处,其中30处最大积水深度超过1.5 m;积水路段73处,其中桥西区18处,新华区16处,桥东区7处,长安区17处,裕华区15处。积水淹没面积193.38 km2,最终积水量1.05亿m3,其中农田淹没面积9 268.21 hm2,房屋淹没面积1 763.35万m2,研究计算结果可为防汛部门应急管理提供关键技术支撑。
3.4 情景模拟危险性分析参照倪丽丽等[15]基于石家庄局部城区的城市暴雨内涝规划应对研究成果以及刘敏等[16]关于内涝危险性评估等级划分的研究,将石家庄内涝危险性等级划分为3级(如表 2所示),根据100年一遇12 h暴雨积水模拟结果,危险性分析成果如图 12和表 3所示。
| 表 2 危险性分析等级划分 Table 2 Classification of risk analysis |

|
图 12 100年一遇12 h降雨情景危险性分析 Figure 12 Risk analysis of 12 h rainfall of 100-year return period design flood |
| 表 3 危险性分析结果 Table 3 Results of risk analysis |
由表 3可见,100年一遇降雨情景中,大部分受淹区域淹没历时均超过1 h,高风险区域的淹没面积最大,中风险区域次之,低风险区域的淹没面积最小。高风险淹没区域中,淹没水深超过0.5 m的区域面积占到高风险区总面积的一半以上,约为城区总淹没面积的1/3,说明石家庄市主城区100年一遇12 h降雨积涝程度很深、积涝风险很大。由图 12可知,高危险区域主要为新华区东南部、桥西区北部及东部五支渠沿线、桥东区中部、裕华区中部石栾公路沿线以及长安区石黄高速部分路段路基处。
4 结语针对城市暴雨内涝形成、演进及风险特点,基于高精度地形数据,采用小尺度结构化网格剖分研究区域并真实体现城市各地物的实际高程与分布特征。通过径流系数与糙率分区、细化排水分区、合理概化管网与泵站抽排水能力等多类精细化措施,建立了城市暴雨内涝精细化水动力模型,利用“96.8”降雨实测资料与模拟值对比分析,验证了模型的精细化、合理性与可靠性,并成功将其应用于石家庄市主城区暴雨内涝积水风险模拟中。
对石家庄市主城区100年一遇12 h暴雨内涝情景进行模拟,计算结果较好地反映了屋面雨水下排、房屋建筑与线状地物阻水、庭院雨水出流、地道桥等低洼处的汇水积涝、城市道路路面行涝、管网排水以及泵站抽排水等具有典型城市特征的水流现象。根据暴雨积水计算结果,分析了积水点、积水路段、易形成局部积水区域以及淹没面积和影响人口,划分了内涝危险性等级,研究成果可为石家庄市主城区城市规划与内涝防控提供重要决策支持。所建城市暴雨内涝精细化水动力模型,合理考虑并概化了城区各类地物,较好地反映了城区暴雨积水动态过程,模拟精度较高,可推广应用于模拟类似城区的暴雨内涝积水风险。
| [1] |
汪宗伟, 刘焱. 给水排水与城市防灾减灾[J]. 江苏建筑, 2012(3): 24-28. ( WANG Zongwei, LIU Yan. Water supply and sewerage and urban disaster prevention and mitigation[J]. Jiangsu Construction, 2012(3): 24-28. (in Chinese)) |
| [2] |
杨士弘. 城市生态环境学[M]. 北京: 科学出版社, 1996: 56-61. ( YANG Shihong. Urban ecological environment[M]. Beijing: Science Press, 1996: 56-61. (in Chinese))
|
| [3] |
仇劲卫, 李娜, 程晓陶, 等. 天津市城区暴雨沥涝仿真模拟系统[J]. 水利学报, 2000(11): 342-421. ( QIU Jinwei, LI Na, CHENG Xiaotao, et al. The simulation system for heavy rainfall in Tianjin City[J]. Journal of Hydraulic Engineering, 2000(11): 342-421. (in Chinese)) |
| [4] |
解以扬, 李大鸣, 李培彦, 等. 城市暴雨内涝数学模型的研究与应用[J]. 水科学进展, 2005, 16(3): 384-390. ( XIE Yiyang, LI Daming, LI Peiyan, et al. Research and application of mathematical model for urban rainstorm water logging[J]. Advances in Water Science, 2005, 16(3): 384-390. (in Chinese)) |
| [5] |
邱绍伟, 董增川, 李娜, 等. 暴雨洪水仿真模型在上海防汛风险分析中的应用[J]. 水力发电, 2008, 34(5): 11-14. ( QIU Shaowei, DONG Zengchuan, LI Na, et al. Storm flood simulation model in Shanghai flood control and risk analysis[J]. Water Power, 2008, 34(5): 11-14. (in Chinese)) |
| [6] |
DONNEL B P, LETTER J V, MCANALLY W H, et al. Users guide for RMA2 Version 4[M]. US Army Engineer Research and Development Center, 2005: 1-98.
|
| [7] |
何文华. 城市化对济南市暴雨洪水的影响及其洪水模拟研究[D]. 广州: 华南理工大学, 2010: 9-15 (HE Wenhua. Study on urbanization impact and flood simulation of Jinan rainstorm[D]. Guangzhou: South China University of Technology, 2010: 9-15. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10561-2010228531.htm
|
| [8] |
黄清雨, 董军刚, 李梦雅, 等. 暴雨内涝危险性情景模拟方法研究——以上海中心城区为例[J]. 地球信息科学学报, 2016, 18(4): 506-513. ( HUANG Qingyu, DONG Jungang, LI Mengya, et al. Research on the scenario simulation method of rainstorm waterlogging hazard: a case study in the central urban area of Shanghai[J]. Journal of Geo-Information Science, 2016, 18(4): 506-513. (in Chinese)) |
| [9] |
喻海军. 城市洪涝数值模拟技术研究[D]. 广州: 华南理工大学, 2015: 11-12 (YU Haijun. Research on numerical simulation technology of urban floods[D]. Guangzhou: South China University of Technology, 2015: 11-12. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10561-1015986910.htm
|
| [10] |
黄远东, 张洪武, 赵连军, 等. 黄河下游平面二维非恒定输沙数学模型: Ⅰ—模型方程与数值方法[J]. 水动力学研究与进展(A辑), 2003, 18(5): 639-646. ( HUANG Yuandong, ZHANG Hongwu, ZHAO Lianjun, et al. A two-dimensional mathematical model for unsteady sediment transport in the lower Yellow River: Ⅰ-model equations and numerical method[J]. Chinese Journal of Hydronamics (SerA), 2003, 18(5): 639-646. (in Chinese)) |
| [11] |
HUANG Yuandong. Research on two-dimensional mathematical model for sediment transport in the lower Yellow River[J]. Beijing: Tsinghua University, 2001, 56-58. |
| [12] |
衣秀勇, 关春曼, 果有娜, 等. DHI MIKE FLOOD洪水模拟技术应用与研究[M]. 北京: 中国水利水电出版社, 2014: 8-10. ( YI Xiuyong, GUAN Chunman, GUO Youna, et al. DHI MIKE FLOOD flood simulation technology application and research[M]. Beijing: China Water Power Press, 2014: 8-10. (in Chinese))
|
| [13] |
苑希民, 田福昌, 王丽娜. 漫溃堤洪水联算全二维水动力模型及应用[J]. 水科学进展, 2015, 26(1): 83-90. ( YUAN Ximin, TIAN Fuchang, WANG Lina. Comprehensive two-dimensional associate hydrodynamic models for overflow and levee-breach flood and its application[J]. Advances in Water Science, 2015, 26(1): 83-90. (in Chinese)) |
| [14] |
GB 50014—2006室外排水设计规范(2014版)[S]. (GB 50014—2006 Code for design of outdoor wastewater engineering (2014 Ed) [S]. (in Chinese))
|
| [15] |
倪丽丽, 曾坚, 张彦平, 等. 基于精细模型的城市暴雨内涝规划应对——以石家庄局部城区为例[J]. 城市发展研究, 2015, 22(6): 7-8. ( NI Lili, ZENG Jian, ZHANG Yanping, et al. Planning strategies on urban rainstorm water-logging based on fine model: a case study on the part of Shijiazhuang[J]. Urban Development Studies, 2015, 22(6): 7-8. (in Chinese)) |
| [16] |
刘敏, 权瑞松, 徐世远. 城市暴雨内涝灾害风险评估:理论、方法与实践[M]. 北京: 科学出版社, 2012. ( LIU Min, QUAN Ruisong, XU Shiyuan. Urban storm waterlogging disaster risk assessment: theory, methods and practice[M]. Beijing: Science Press, 2012. (in Chinese))
|
2. The Second Design and Research Institute of Water Conservancy and Hydropower of Hebei Province, Shijiazhuang 050021, China
 2017
2017 
