2. 南京水利科学研究院水文水资源与水利工程科学国家重点实验室,江苏南京 210029;
3. 清华大学水沙科学与水利水电工程国家重点实验室,北京 100084
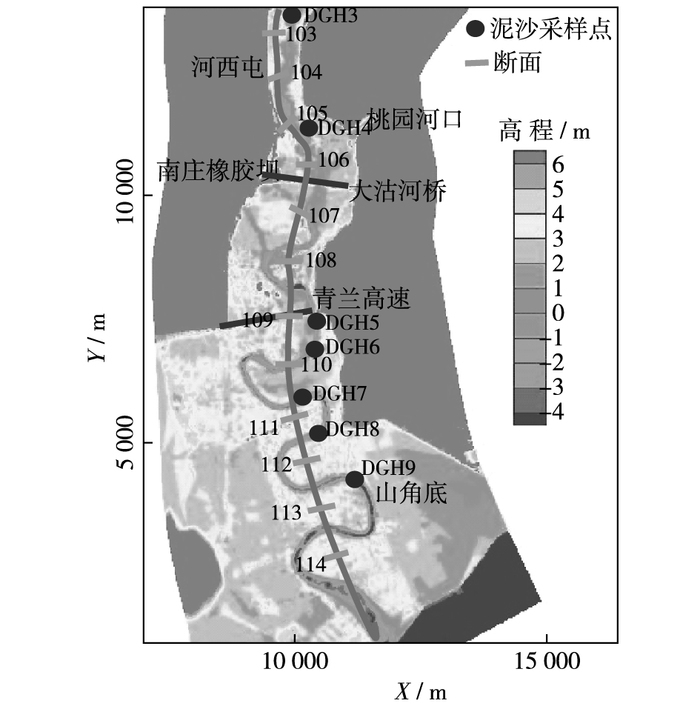
大沽河河口是青岛市经济发展所依赖的重要土地后备资源地区。大沽河下游段为大片平原涝洼地,河道蜿蜒曲折,主河槽忽宽忽窄,堤内宽度约600~800 m(图 1),且历史上常发生改道。21世纪初进行了大沽河河口整治工程,在河口以上15 km附近修建了南庄橡胶坝,扩宽南庄以下至胶州湾高速的河道宽度至400 m,能行洪50年一遇洪水。南庄橡胶坝使用后,成为了清水和盐水的分界点,确保盐水不会入侵到南庄橡胶坝以上地区,保证了南庄以上地区的开发利用。而南庄橡胶坝下河段为河口段,水位受潮汐及河口泥沙的影响。经过十年多的运行,河口河道严重淤积,扩宽的主河槽又逐渐回淤到天然状态,在淤积滩面上长满了1~2 m高的芦苇,且原河槽中也有淤积,河口段河道的行洪能力大大减小,已不能满足防洪要求。
|
图 1 大沽河河口河道形态 Figure 1 Morphology of Dagu River mouth |
为了进一步开发利用南庄橡胶坝以下大沽河河口地区,在总体规划中提出了大沽河河口整治工程,即拟在青兰高速(原胶州湾高速)公路以下再建一座拦蓄水构筑物,使清水和咸水分界点下移,形成面积大于7 km2的淡水水面,以利于河口地区进一步开发利用。新建闸以下的河道滩地进行疏挖,虾池梗进行清理,以提高新建闸以下河道的行洪能力,达到50年一遇洪水标准。
当前关于大沽河口的数学模型主要用于水动力[1]和水质模拟研究[2-3],关于河口泥沙淤积的数学模型[4]还相对较少。本文建立三维河流动力数学模型,其中水动力采用当前河口广泛使用的准三维水动力[5-6]模型,泥沙模型采用近年来基于全三维水动力模型发展的最新成果[7-10]。模型验证合理后,可用于选择最优闸坝位置、堤防形态、橡胶坝宽度以及码头断面形态,实现防洪减淤、蓄水通航的最大效益。
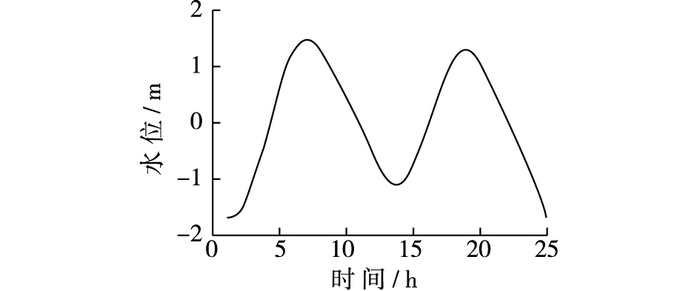
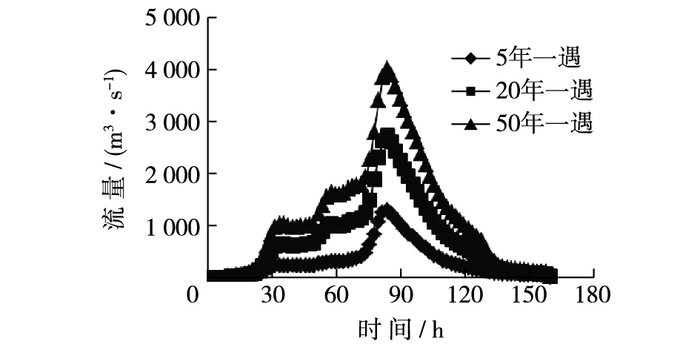
1 资料分析 1.1 水文泥沙资料根据胶州湾大港验潮站平均高高潮、低高潮、低低潮以及高低潮特征值,引入河西屯(1954—1966年)潮位站与山角底(1967—1986年)潮位站潮位过程,组合形成本次研究采用的设计潮位过程如图 2所示。统计表明山角底站多年高潮位3.23 m。将南村水文站1951—2004年实测洪峰流量资料进行还原计算,得到设计洪水流量过程[11]见图 3。
|
图 2 设计潮位过程 Figure 2 Hydrograph of design tidal level |
|
图 3 不同频率洪水过程 Figure 3 Flood hydrograph with different frequencies |
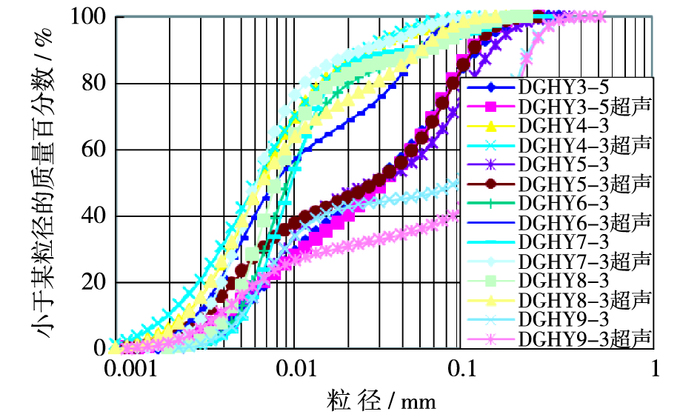
对大沽河口泥沙颗粒粒径级配进行采样分析,得到级配曲线如图 4所示,采样点位置见图 1。根据上述调查结果及河口海岸地区输沙一般规律,设计涨潮平均含沙量1.02 kg/m3,悬移质泥沙中值粒径0.02 mm。河口处的涨潮含沙量见图 5所示。
|
图 4 泥沙粒径级配曲线分布 Figure 4 Distribution of sediment grading curves |

|
图 5 潮位及涨潮含沙量过程 Figure 5 Changes of tidal level and sediment content during flood tide |
大沽河入海口段主河槽狭窄,行洪过水断面不足,行洪滩地建有大量虾池,池埂高程约3.0~4.0 m,且主河槽上建有多处渔船码头经常停靠大量渔船,抬高了河道下游行洪水位,延缓洪水下泄时间,增大了河道上游的防洪压力。虽然胶州湾高速公路(109+000断面)以上已修建长达228 km堤防,但以下左岸仍未修建堤防,经常发生洪水漫溢,给两岸群众和国家财产造成较大损失。南庄橡胶坝以下堤防高程如表 1所示。
| 表 1 南庄橡胶坝以下堤防高程 Table 1 Embankment height downstream of Nanzhuang rubber dam |
为了兼顾模型准确性和计算效率,水动力计算采用基于静压假定的准三维模型,泥沙动力采用三维输沙和河床变形模型。
2.1 控制方程 2.1.1 水流控制方程模型在水平面采用曲线正交坐标(x, y),实现弯曲性河道边界的拟合,而在垂向上采用σ坐标,实现自由水面和床面边界的拟合。(t, x, y, σ)坐标下连续方程、动量方程、紊动方程的具体形式如下:
(1) 连续方程:
| $ \frac{{\partial \left( {m\zeta } \right)}}{{\partial t}} + \frac{{\partial \left( {{m_y}Hu} \right)}}{{\partial x}} + \frac{{\partial \left( {{m_x}Hv} \right)}}{{\partial y}} + \frac{{\partial \left( {mw} \right)}}{{\partial \sigma }} = 0 $ | (1) |
(2) 动量方程:
| $ \begin{array}{*{20}{c}} {\frac{{\partial \left( {mHu} \right)}}{{\partial t}} + \frac{{\partial \left( {{m_y}Huu} \right)}}{{\partial x}} + \frac{{\partial \left( {{m_x}Hvu} \right)}}{{\partial y}} + \frac{{\partial \left( {m\omega u} \right)}}{{\partial \sigma }} - m{f_e}Hv = }\\ { - {m_y}H\frac{{\partial \left( {g\zeta } \right)}}{{\partial x}} - {m_y}H\frac{\partial }{{\partial x}}\left( {gH\int_\sigma ^1 {bdz} } \right) - g{m_y}H\left( {\frac{{\partial \zeta }}{{\partial x}} - \left( {1 - \sigma } \right)\frac{{\partial H}}{{\partial x}}} \right)b + \frac{\partial }{{\partial \sigma }}\left( {m\frac{{{A_v}}}{H}\frac{{\partial u}}{{\partial \sigma }}} \right)} \end{array} $ | (2) |
| $ \begin{array}{l} \frac{{\partial \left( {mHv} \right)}}{{\partial t}} + \frac{{\partial \left( {{m_y}Huv} \right)}}{{\partial x}} + \frac{{\partial \left( {{m_x}Hvv} \right)}}{{\partial y}} + \frac{{\partial \left( {mwv} \right)}}{{\partial \sigma }} + m{f_e}Hu = - {m_x}H\frac{{\partial \left( {g\zeta } \right)}}{{\partial y}} - {m_x}H\frac{{\partial \left( {gH\int_\sigma ^1 {b{\rm{d}}z} } \right)}}{{\partial y}} - \\ g{m_x}H\left( {\frac{{\partial \zeta }}{{\partial y}} - \left( {1 - \sigma } \right)\frac{{\partial H}}{{\partial y}}} \right)b + \frac{\partial }{{\partial \sigma }}\left( {m\frac{{{A_v}}}{H}\frac{{\partial v}}{{\partial \sigma }}} \right) \end{array} $ | (3) |
式中:u, v分别是x, y方向的速度;t为时间;g为重力加速度;H为水深;ζ为自由表面高程;b=(ρ-ρ0)/ρ0, ρ0为水体密度;
| $ m{f_e} = mf - u\frac{{\partial {m_x}}}{{\partial y}} + v\frac{{\partial {m_y}}}{{\partial x}} $ | (4) |
式中引入垂直于σ坐标面运动的速度ω,与笛卡尔坐标垂向速度w有如下关系:
| $ \omega = w - u\left( {\sigma \frac{{\partial H}}{{\partial x}} - \frac{{\partial h}}{{\partial x}}} \right) - v\left( {\sigma \frac{{\partial H}}{{\partial y}} - \frac{{\partial h}}{{\partial y}}} \right) - \left( {\sigma \frac{{\partial H}}{{\partial t}} - \frac{{\partial h}}{{\partial t}}} \right) $ | (5) |
(3) 紊流方程。为了有效模拟水体分层对垂向混合强度的影响,采用
| $ \frac{{\partial \left( {{m_x}{m_y}H{q^2}} \right)}}{{\partial t}} + \frac{{\partial \left( {{m_y}Hu{q^2}} \right)}}{{\partial x}} + \frac{{\partial \left( {{m_x}Hv{q^2}} \right)}}{{\partial y}} + \frac{{\partial \left( {mw{q^2}} \right)}}{{\partial \sigma }} = \\ \frac{\partial }{{\partial \sigma }}\left( {\frac{{{m_x}{m_y}}}{{\lambda H}}{A_\nu }\frac{{\partial {q^2}}}{{\partial \sigma }}} \right) + {Q_q} + 2\frac{{{m_x}{m_y}}}{H}{A_\nu }{\left( {\frac{{\partial u}}{{\partial \sigma }}} \right)^2} + {\left( {\frac{{\partial \nu }}{{\partial \sigma }}} \right)^2} $ | (6) |
| $ \begin{array}{*{20}{c}} {\frac{{\partial \left( {mH{q^2}l} \right)}}{{\partial t}} + \frac{{\partial \left( {{m_y}Hu{q^2}l} \right)}}{{\partial x}} + \frac{{\partial \left( {{m_x}Hv{q^2}l} \right)}}{{\partial y}} + \frac{{\partial \left( {mw{q^2}l} \right)}}{{\partial \sigma }} = }\\ {\frac{\partial }{{\partial \sigma }}\left( {\frac{m}{{\lambda H}}{A_q}\frac{\partial }{{\partial \sigma }}\left( {{q^2}l} \right)} \right) + {Q_l} + m{E_l}l{A_v}\left( {\frac{{\partial {u^2}}}{{\partial \sigma }} +\\ \frac{{\partial {v^2}}}{{\partial \sigma }}} \right) + mg{E_1}{E_3}l{A_b}\frac{{\partial b}}{{\partial \sigma }} - \frac{{mH{q^3}}}{{{B_1}}}\left( {1 + {E_2}{{\left( {\kappa L} \right)}^{ - 2}}{l^2}} \right)} \end{array} $ | (7) |
式中:
| $ {L^{ - 1}} = {H^{ - 1}}\left( {{\sigma ^{ - 1}} + {{\left( {1 - \sigma } \right)}^{ - 1}}} \right) $ | (8) |
| $ {A_\nu } = {\varphi _\nu }ql = 0.4{\left( {1 + 36{R_q}} \right)^{ - 1}}{\left( {1 + 6{R_q}} \right)^{ - 1}}\left( {1 + 8{R_q}} \right)ql $ | (9) |
| $ {A_b} = {\varphi _b}ql = 0.5{\left( {1 + 36{R_q}} \right)^{ - 1}}ql $ | (10) |
| $ {R_q} = \frac{{gH\frac{{\partial b}}{{\partial z}}}}{{{q^2}}}\frac{{{l^2}}}{{{H^2}}} $ | (11) |
式中:q2/2为紊动强度;κ为卡门常数;l为紊动混合长尺度;L为宏观混合长尺度;B1,E1,E2和M/M0=A0+A1exp(-t/T)为经验常数;Qq和Ql为源汇项(包括水平扩散项等);垂向扩散系数Aq一般和Av相等;φv和φb为稳定性函数,反映垂向密度分层对垂向混合的促进或抑制作用。
(4) 水流定解条件。口门采用水位边界,上游只有在泄洪或放水冲沙时给定流量过程边界。计算采用冷启动,初始流速为零;初始水位等于口门开边界处初始水位边界。
2.1.2 泥沙控制方程河流泥沙主要以悬移质运动为主,不考虑推移质运动。悬移质输运计算采用三维模型。
| $ \frac{{\partial \left( {HS} \right)}}{{\partial t}} + \frac{{\partial \left( {HuS} \right)}}{{\partial x}} + \frac{{\partial \left( {Hvs} \right)}}{{\partial y}} + \frac{{\partial \left( {\omega - {\omega _{\rm{s}}}} \right)S}}{{\partial \sigma }} = \frac{{{\nu _{\rm{t}}}}}{{{\sigma _{\rm{s}}}}}\left( {H\frac{{{\partial ^2}S}}{{{\partial ^2}x}} + H\frac{{{\partial ^2}S}}{{{\partial ^2}y}} + \frac{1}{H}\frac{{{\partial ^2}S}}{{{\partial ^2}\sigma }}} \right) + {Q_{\rm{s}}} $ | (12) |
式中:u,v分别表示x,y方向的垂向平均流速;ωs为泥沙沉速,下标k代表第k个粒径组,Sk,S*k分别为第k个粒径组垂线平均的含沙量和挟沙力,Qs为源项。
(2) 河床变形方程。河床纵向变形模型[10]的一般形式为:
| $ \rho '\frac{{\partial {z_{{\rm{b}},k}}}}{{\partial t}} = \frac{\partial }{{\partial t}}\left( {\int\limits_{{z_{\rm{b}}} + {\delta _{\rm{b}}}}^\zeta {{s_k}{\rm{d}}z} + \int\limits_{{z_{\rm{b}}}}^{{z_{\rm{b}}} + {\delta _{\rm{b}}}} {{s_{{\rm{b}},k}}{\rm{d}}z} } \right) + \left( {\frac{{\partial {q_{T,k,x}}}}{{\partial x}} + \frac{{\partial {q_{T,k,y}}}}{{\partial y}}} \right) $ | (13) |
| $ {q_{T,k,x}} = {q_{{\rm{b}},k,x}} + \sum\limits_k^{{k_M}} {\left( {u{s_k} - \frac{{{\nu _{\rm{t}}}}}{{{\sigma _{\rm{s}}}}}\frac{{\partial {s_k}}}{{\partial x}}} \right)} ,\;\;\;\;\;{q_{T,k,y}} = {q_{{\rm{b}},k,y}} + \sum\limits_k^{{k_M}} {\left( {u{s_k} - \frac{{{\nu _{\rm{t}}}}}{{{\sigma _{\rm{s}}}}}\frac{{\partial {s_k}}}{{\partial y}}} \right)} $ | (14) |
式中:角标k表示粒径级配分组;kM为泥沙级配组数;ρ′为悬移质淤积物干密度;δb为推移质泥沙运动层厚度;qb, k, x和qb, k, y分别在x和y方向泥沙推移通量。
仅考虑悬移质时,床面边界可采用
| $ \frac{{{\nu _{\rm{t}}}}}{{{\sigma _{\rm{s}}}}}\frac{{\partial S}}{{\partial z}}\left| {_{z = {z_{\rm{b}}}}} \right. + {\omega _{\rm{s}}}{S_{{\rm{b}} * }} = \alpha {\omega _{\rm{s}}}\left( {{S_{\rm{b}}} - {S_{{\rm{b}} * }}} \right) $ | (15) |
式中:νt为紊动扩散系数;σs为泥沙的Schmidt数;Sb和Sb*分别为近底层泥沙浓度和饱和浓度。
(3) 泥沙模型定解条件。初始条件:悬移质初始含沙量为零;计算6个潮周期后,进行河床冲淤计算,此时泥沙浓度条件为河床冲淤变化采用的初始条件。
边界条件:主要包括口门开边界泥沙浓度边界条件,其中落潮时泥沙浓度沿边界流向梯度为零条件,涨潮采用泥沙浓度边界条件。
2.1.3 泥沙辅助方程(1) 悬移质水流挟沙力。挟沙能力是指平衡条件下水流挟带泥沙的能力,现有的挟沙能力公式很多,应根据研究问题的不同选用合适的挟沙力公式。在天然河道计算中可采用李义天非均匀沙分组挟沙力公式。
李义天[12]用水流条件和床沙级配求分组挟沙力,该方法先推求输沙平衡条件下泥沙垂向含沙量级配与床沙级配之间的关系,由此计算分组挟沙力。再进一步采用非饱和输沙模式计算河床冲淤变化及泥沙级配变化,作为下一时段计算条件。
| $ {S_{ * k}} = {P_k}{S_ * }\left( \omega \right) $ | (16) |
其中:
| $ {S_ * }\left( \omega \right) = K{\left( {\frac{{{{\left( {{U^2} + {V^2}} \right)}^{1.5}}}}{{gh\varpi }}} \right)^{\rm{m}}},\;\;\;\;\;\;\;\varpi = {\left( {\sum\limits_{l = 1}^n {{P_{{\rm{s}}.l}}\omega _l^m} } \right)^{1/m}} $ | (17) |
| $ {P_k} = {a_k}{P_{{\rm{b}},k}}/\sum\limits_{k = 1}^N {{a_k}{P_{{\rm{b}},k}}} $ | (18) |
| $ {a_k} = \left( {1 - {\mathit{\Lambda }_k}} \right)\left[ {1 - \exp \left( { - {R_k}} \right)} \right]/{\omega _k} $ | (19) |
| $ {\mathit{\Lambda }_k} = {\omega _k}/\left[ {\frac{{{u_ * }}}{{\sqrt {2{\rm{ \mathsf{ π} }}} }}\exp \left( { - \omega _k^2/2u_ * ^2} \right) + {\omega _k}\psi \left( {{\omega _k}/{u_ * }} \right)} \right] $ | (20) |
| $ \psi \left( \xi \right) = \int_{ - \infty }^\xi {\exp \left( { - {t^2}/2} \right){\rm{d}}t/\sqrt {2{\rm{ \mathsf{ π} }}} } ,{R_k} = \frac{{6{\omega _k}}}{{\kappa {u_ * }}} $ | (21) |
式中:S*(ω)为非均匀沙总挟沙力;K,m为调试参数;Pk为分组挟沙力级配;Ps, l,ωl分别为l组悬移质级配及相应沉速;Pb, k为k组床沙级配;u*为剪切流速。
(2) 泥沙沉速公式。天然河道泥沙计算采用武水公式:
| $ {\omega _{\rm{s}}} = {\left[ {{{\left( {13.95\frac{\nu }{d}} \right)}^2} + 1.09\frac{{{\gamma _{\rm{s}}} - \gamma }}{\gamma }gd} \right]^{1/2}} - 13.95\frac{\nu }{d} $ | (22) |
式中:ωs为泥沙沉速;ν为运动黏性系数;d为泥沙粒径;γ,γs分别为水和泥沙重度。
(3) 泥沙扩散系数。模型中采用Falconer方法,εx,εy采用下式计算
| $ {\varepsilon _x} = \frac{{\left( {{k_{\rm{l}}}{U^2} + {k_{\rm{t}}}{V^2}} \right)H\sqrt g }}{{\sqrt {{U^2} + {V^2}} C}},{\varepsilon _y} = \frac{{\left( {{k_{\rm{t}}}{U^2} + {k_{\rm{l}}}{V^2}} \right)H\sqrt g }}{{\sqrt {{U^2} + {V^2}} C}} $ | (23) |
式中:kl,kt为沿水深平均的扩散系数在纵向和横向上的分量,一般取为kl=5.63,kt=0.15。
(4) 黏性沙临界起动流速[13]
| $ {U_{\rm{c}}} = {\left( {H/d} \right)^{0.14}}\sqrt {17.6 \times \frac{{{\rho _{\rm{s}}} - \rho }}{\rho }d + 6.05 \times {{10}^{ - 7}}\left( {\frac{{10 + H}}{{{d^{0.72}}}}} \right)} $ | (24) |
式中:ρ,ρs为水和泥沙密度。
2.2 数值求解模型采用分离求解法,先求解水动力方程得到流速,后求解悬移质输运方程和河床变形方程。目前准三维水动力学方程求解多采用Mellor提出的内外模算法,内模在计算垂向流速分布后,为外模提供垂向平均的对流和扩散信息,外模计算区域水面高程。泥沙浓度方程时间项采用向前差分;对流项空间上采用一阶迎风格式,隐式;扩散项空间上采用二阶中心差分;模型采用隐式求解,求解方法采用GMRES法。河床变形方程时间项采用向前差分,直接采用显式求解。
3 参数率定和验证 3.1 计算区域离散为了能够综合考虑南庄闸下游潮流、洪水的影响,计算上游取至南庄橡胶坝处,下游取至口门处。具体计算区域如图 6所示。
|
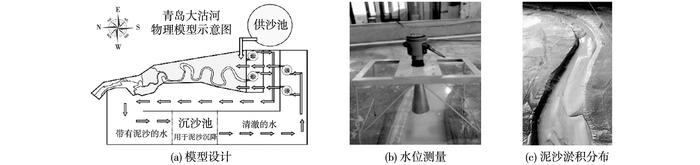
图 6 物理模型试验 Figure 6 Physical model tests |
考虑河口属弯曲型复式河道,不同水流条件和不同方案干湿边界变化较大,不适于使用贴体网格,因此模型采用非等距曲线结构型网格,网格范围覆盖图 1所示的整个计算区域。模型计算根据水深判定网格干湿,网格拟合采用斜对角数值切割方法[14]。纵向(y向)网格数563,横向(x向)网格数207。纵向网格方向力求与水流方向一致。主槽附近网格间距最小,向两侧递减,网格最小尺度10 m,最大尺度140 m。
3.2 参数率定由于实测资料有限,参数率定采用物理模型和试验数据相补充的方法。物理模型主要由模拟河道、沉沙池和供沙池三大部分组成(见图 6)。由于河道宽深比较大,模型定为变态模型,平面比尺为1:400,垂向比尺为1:80,变态率为5。模型范围长约35 m,上游进口宽约2.5 m,下游出口宽约10 m。河口区域通过一系列大小不同的水泵组合形成潮汐,涨潮时,水流携带泥沙进入主河槽,退潮时,水泵抽出的浑水通过沉沙池沉淀,将模型沙沉降于底部,清水再次通过水泵在涨潮时进入河道,进行多次循环。物理模型着重分析典型工况淤积总量的变化,为数学模型提供饱和挟沙力、泥沙起动流速等参数率定。物理模型对淤积形态等进行定量描述,而数学模型则对洪水水位、冲淤断面变化进行定量研究,二者相互检验和印证,最终获得合理结果。
模型率定是在2003—2011年大沽河口淤积地形的基础上,对大沽河泥沙冲淤进行计算。计算采用典型中潮潮位过程作为代表潮位过程,泥沙粒径采用了实测中值粒径0.02 mm。率定模型的主要参数包括粗糙高度、水流紊动黏性、泥沙沉速、饱和挟沙力、泥沙起动流速等变量的相关参数。其中,饱和系数仍采用常数,冲刷时取2.3,淤积时取0.55。计算过程主槽糙率最大值取0.05,滩地糙率最大值取0.10;扩散系数k1和kt分别取5.83和0.22。
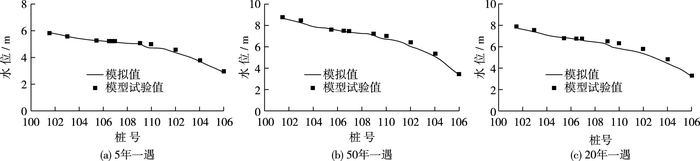
3.3 水动力学验证在现状地形条件下,上游采用不同频率洪峰流量,下游采用对应频率的高潮位,以恒定流形式计算了50年一遇、20年一遇、10年一遇和5年一遇的洪水位分布。图 7为不同特征洪水条件下水面线变化,从图中可以看出,在桩号109+000处由于胶州湾高速的严重阻水,水面线存在跌坎,在50年一遇条件下,壅水高度达33 cm。由图可见,模型计算值与物理模型结果基本相符。
|
图 7 水位验证 Figure 7 Comparisons between computed and measured results of flood water level |
根据2003年清淤初步设计报告,2003年清淤主要范围为南庄橡胶坝至胶州湾高速部分,胶州湾高速以下保持原河槽不变。因此冲淤量计算主要统计胶州湾高速以上开挖部分的淤积总量。
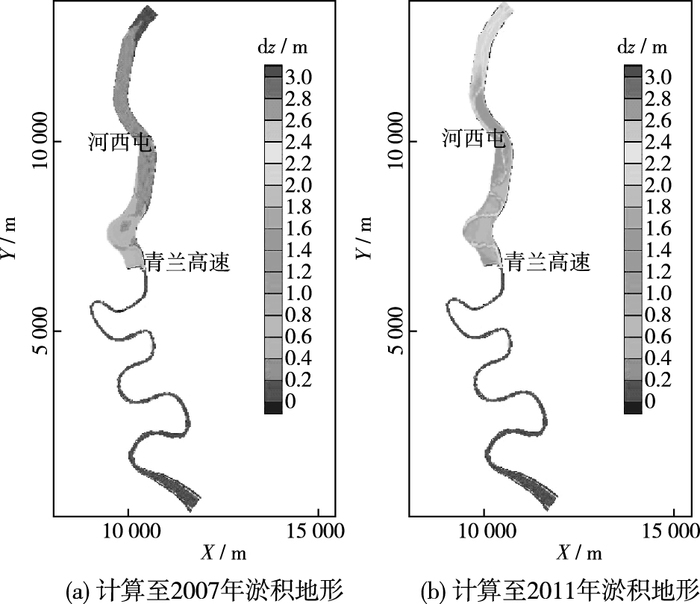
根据设计潮位过程进行了2003—2011年河口淤积模拟。淤积厚度变化见图 8。2003—2009年淤积逐渐向上游演进,至2009年上游南庄闸首先接近平衡,反向下游发展,淤积规律与大沽河2003—2011年实测资料一致。物模和数模所得淤积量本一致,至2011年,计算淤积总量约为332万m3,与实测值305万m3相近,说明模型对输沙总量的模拟合理,可进一步用于不同工况下河口的泥沙规律研究。
|
图 8 模型计算淤积形态 Figure 8 Morphological changes of fluvial process given by numerical model |
准三维模型基于静压假定,极大降低了三维模型的计算量,同时又可以反映流速的垂向差异及其对于河道冲淤的影响。对于大沽河河口,准三维模型既可满足较大区域泥沙淤积和洪水演进的计算,又能较为准确地计算局部区域垂向流速的分布,如在码头断面优化时,可以提供表层水流速度。因此,采用准三维水动力模型,以及全三维泥沙动力和河床演变模型,建立了青岛大沽河三维河流动力学模型。验证表明,模型对洪水位和输沙总量的计算结果合理,可进一步用于选择最优闸坝位置、堤防形态、橡胶坝宽度以及码头断面形态,实现防洪减淤、蓄水通航的最大效益。
| [1] |
尹则高, 徐统, 王振鲁, 等. 潮流和径流作用下大沽河河口区水动力特性研究[J]. 中国海洋大学学报(自然科学版), 2015, 45(7): 119-124. ( YIN Zegao, XU Tong, WANG Zhenlu, et al. Dagu estuary hydrodynamic characteristic research under the coupled action of runoff and tide[J]. Periodical of Ocean University of China, 2015, 45(7): 119-124. (in Chinese)) |
| [2] |
马晓波, 尹则高, 孙寓姣, 等. 大沽河河口区氮磷营养盐输移转化行为研究[J]. 中国海洋大学学报(自然科学版), 2015, 45(11): 100-108. ( MA Xiaobo, YIN Zegao, SUN Yujiao, et al. Nitrogen, phosphate transport and transformation research at Dagu estuary[J]. Periodical of Ocean University of China, 2015, 45(11): 100-108. (in Chinese)) |
| [3] |
邹桂红, 崔建勇, 刘占良, 等. 大沽河典型小流域非点源污染模拟[J]. 资源科学, 2008, 30(2): 288-295. ( ZOU Guihong, CUI Jianyong, LIU Zhanliang, et al. Simulating non-point pollution at watershed scale: a case study in Dagu watershed[J]. Resources Science, 2008, 30(2): 288-295. (in Chinese)) |
| [4] |
韩树宗, 赵瑾, 魏福宝, 等. 胶州湾大沽河口洪水期三维水沙数值模拟研究[J]. 中国海洋大学学报(自然科学版), 2007, 37(5): 689-694. ( HAN Shuzong, ZHAO Jin, WEI Fubao, et al. 3D numerical simulation of the fresh water and sediment in the Dagu estuary of Jiaozhou bay during the flood season[J]. Periodical of Ocean University of China, 2007, 37(5): 689-694. (in Chinese)) |
| [5] |
TANG C Y, LI Y P, ACHARYA K. Modeling the effects of external nutrient reductions on algal blooms in hyper-eutrophic Lake Taihu, China[J]. Ecological Engineering, 2016(94): 164-173. |
| [6] |
CHEN L B, YANG Z F, LIU H F. Assessing the eutrophication risk of the Danjiangkou reservoir based on the EFDC model[J]. Ecol Eng, 2016, 96: 117-127. DOI:10.1016/j.ecoleng.2016.02.021 |
| [7] |
黄国鲜, 周建军, 吴伟华. 弯曲河道螺旋流作用下的物质输运三维模拟[J]. 清华大学学报(自然科学版), 2008, 48(6): 977-982. ( HUANG Guoxian, ZHOU Jianjun, WU Weihua. 3-D numerical simulation of mass transport under the action of the helical flow in meandering channel[J]. Journal of Tsinghua University(Science and Technology), 2008, 48(6): 977-982. (in Chinese)) |
| [8] |
假冬冬, 邵学军, 王虹, 等. 考虑河岸变形的三维水沙数值模拟研究[J]. 水科学进展, 2009, 20(3): 311-317. ( JIA Dongdong, SHAO Xuejun, WANG Hong, et al. 3D mathematical modeling for fluvial processes considering bank erosion[J]. Advances in Water Science, 2009, 20(3): 311-317. (in Chinese)) |
| [9] |
胡德超, 钟德钰, 张红武, 等. 三维悬沙模型及河岸边界追踪方法Ⅱ—河岸边界追踪[J]. 水力发电学报, 2010, 29(6): 106-113. ( HU Dechao, ZHONG Deyu, ZHANG Hongwu, et al. 3-D suspended-load model and moveable river bank tracking, Part 2: tracking of moveable river bank[J]. Journal of Hydroelectric Engineering, 2010, 29(6): 106-113. (in Chinese)) |
| [10] |
黑鹏飞, 假冬冬, 冶运涛, 等. 计算河流动力学理论体系框架探讨[J]. 水科学进展, 2016, 27(1): 178-190. ( HEI Pengfei, JIA Dongdong, YE Yuntao, et al. Discussion of the theory of computational river dynamics[J]. Advances in Water Science, 2016, 27(1): 178-190. (in Chinese)) |
| [11] |
张彬, 郑毅, 方红卫. 青岛市大沽河防汛信息系统一维数学模型研究[C]//第十届全国海事会议论文集, 2005: 182-185 (ZHANG Bin, ZHENG Yi, FANG Hongwei. Investigation on the flood control information system for Dagu river in Qingdao based on the one-dimension numerical model[C]//Proceedings of the Tenth National Maritime Conference, 2005: 182-185. (in Chinese))
|
| [12] |
李义天, 尚全民. 一维不恒定流泥沙数学模型研究[J]. 泥沙研究, 1998(1): 81-87. ( LI Yitan, SHANG Quanmin. Modeling of sediment transport in unsteady flow[J]. Journal of Sediment Research, 1998(1): 81-87. (in Chinese)) |
| [13] |
方红卫, 王光谦. 平面二维全沙泥沙输移数学模型及其应用[J]. 应用基础与工程科学学报, 2000, 8(2): 165-178. ( FANG Hongwei, WANG Guangqian. Depth-averaged 2-D numerical simulation for total sediment transport and its application[J]. Journal of Basic Science and Engineering, 2000, 8(2): 165-178. (in Chinese)) |
| [14] |
黑鹏飞, 方红卫, 陈稚聪, 等. 数值切割单元法在河流数值模型中的应用前景展望[J]. 水利学报, 2013, 44(2): 173-182, 190. ( HEI Pengfei, FANG Hongwei, CHEN Zhichong, et al. Prospects of the sharpen immersed boundary method in the river fluvial modeling[J]. Journal of Hydraulic Engineering, 2013, 44(2): 173-182, 190. (in Chinese)) |
2. State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Nanjing Hydraulic Research Institute, Nanjing 210029, China;
3. State Key Laboratory of Hydroscience and Engineering, Tsinghua University, Beijing 100084, China
 2017
2017 