2. 中国人民武装警察部队水电第二总队,江西南昌 330096
河道堤防工程是人类长期与水涝灾害做斗争的产物,是居民安全生产、生活的保障。堤防失事已成为洪水灾害爆发的一个重要因素。在堤坝溃决后进行迅速有效的封堵,以防御可能的二次洪水袭击、降低堤坝溃决灾害损失。决口抢险需以现场的水力学特性参数为依据,选择合适的封堵方法快速有效地进行[1]。因而通过研究堤防决口不同封堵方法的水力学特性,并据此制定快速且准确有效的抢险封堵措施具有重要意义。堤防决口封堵方法[2]主要分为平堵、立堵和混合堵3种。混合堵法是将立堵与平堵相结合的方法,可取长补短。20世纪40年代以前以平堵为主,50年代后立堵法逐渐被采用并得到广泛应用[3]。
早期堤坝溃决以分析研究溃坝水流运动的理论解为主,但简单依靠理论解解决实际溃决问题并不是很有效[4]。在理论研究基础上,数值模拟求解能较好地弥补一些不足。1986年,Garcia等[5]将数学模型的数值解和基于Saint-Venant方程组的一维无摩擦溃坝解析解进行了对比验证;1992年,Toro[6]通过有限差分法WAF利用TVD形式求解二维溃坝问题;2003年,魏文礼等[7]在求解二维浅水方程基础上建立了模拟大坝瞬间全溃或局部溃倒所致的洪水演进过程数学模型,并预测矩形河道情况下大坝瞬间局部溃倒时下游有多个障碍物的洪水演进过程。2005年,王志力等[8]对存在多处险滩和深潭的地形复杂河段采用非结构化网格有限体积法进行实际模拟,结果吻合较好。2011年,岳志远等[9]基于非结构三角网格系统的非恒定浅水二维水流数学模型对4个经典算例进行模拟。2014年,冶运涛等[10]建立适应于结构网格的复杂边界浅水流动高分辨率高精度有限体积数学模型对非平底地形溃坝水流算例和超临界流倾斜水跃算例进行验证。本文针对长直河道下T形决口,采用数值模拟方法,模拟堤防决口不同封堵方法的封堵过程,对比分析其水力学特性[11]。
1 基本理论FLOW-3D采用独创的FAVOR方法及真实的Tru-VOF方法,具有离散完整的N-S方程,能很好地模拟真实世界中自由液面的流动现象及准确计算出其流场性质。数值模拟选择非恒定、VOF,RNG湍流模型[12-13]。
1.1 基本方程流体为牛顿流体,暂不考虑泥沙问题,基本方程包括连续方程、动量方程[14-15]。
连续方程:
| $\frac{{\partial (u{A_x})}}{{\partial x}} + \frac{{\partial (v{A_y})}}{{\partial y}} + \frac{{\partial (w{A_z})}}{{\partial z}} = 0$ | (1) |
动量方程:
| $\frac{{\partial u}}{{\partial t}} + \frac{1}{{{V_F}}}\{ u{A_x}\frac{{\partial u}}{{\partial x}} + v{A_y}\frac{{\partial u}}{{\partial y}} + w{A_z}\frac{{\partial u}}{{\partial z}}\} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} + {G_x} + {f_x}$ | (2) |
| $\frac{{\partial v}}{{\partial t}} + \frac{1}{{{V_F}}}\{ u{A_x}\frac{{\partial v}}{{\partial x}} + v{A_y}\frac{{\partial v}}{{\partial y}} + w{A_z}\frac{{\partial v}}{{\partial z}}\} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial y}} + {G_y} + {f_y}$ | (3) |
| $\frac{{\partial w}}{{\partial t}} + \frac{1}{{{V_F}}}\{ u{A_x}\frac{{\partial w}}{{\partial x}} + v{A_y}\frac{{\partial w}}{{\partial y}} + w{A_z}\frac{{\partial w}}{{\partial z}}\} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial z}} + {G_z} + {f_z}$ | (4) |
式中:u,v,w分别为x,y,z方向上的流速分量;Ax,Ay,Az分别为x,y,z方向上可流动的面积分数;Gx,Gy,Gz分别为x,y,z方向上的重力和非惯性力加速度;fx,fy,fz分别为x,y,z方向上的黏滞力加速度;VF为可流动的体积分数;ρ为流体密度;p为作用在流体微元上的压强;t为时间。
1.2 RNG k-ε模型FLOW-3D软件本身提供5种紊流模型,采用RNG k-ε模型进行模拟,可以更好地处理流线弯曲较大及高应变率的流动。
紊动能k方程:
| $\frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho k{u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left( {{\alpha _k}{\mu _{{\rm{eff}}}}\frac{{\partial k}}{{\partial {x_j}}}} \right) + {G_k} + \rho \varepsilon $ | (5) |
紊动能耗散率ε方程:
| $\frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho \varepsilon {u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left( {{\alpha _\varepsilon }{\mu _{{\rm{eff}}}}\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right) + \frac{{C_{1\varepsilon }^*\varepsilon }}{k}{G_k} - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k}$ | (6) |
式中:k为紊动能;ε为紊动能耗散率;μ为紊动黏滞系数,μeff=μ+μt,μt=ρCμk2/ε,Cμ=0.084 5;αk,αε分别为湍动能和耗散率对应的Prandtl数,αk=αε=1.39;Gk为紊动能k的产生项,Gk=μt(∂ui/∂xj+∂uj/∂xi)∂ui/∂xj;C1ε*=C1ε-η(1-η/η0)/(1+βη3)为经验常数,C1ε=1.42,C2ε=1.68,η0=4.377,β=0.012。
1.3 自由表面处理技术FLOW-3D软件对自由表面追踪采用VOF法,用体积追踪的方式提高其适用性,可处理流体的破碎和融合。其原理[13]是模型中互不相融的两种或多种流体的任何相位,都有与其相对应的相关变量来描述,计算域整体的流动由所有相位的流动情况相加构成。任一单元的变量和特性取决于每一相的面积和体积分量值及其运动情况。
VOF运动学方程:
| $\frac{{\partial F}}{{\partial t}} + \frac{1}{{{V_F}}}[\frac{{\partial (F{A_x}u)}}{{\partial x}} + \frac{{\partial (F{A_y}v)}}{{\partial y}} + \frac{{\partial (F{A_z}w)}}{{\partial z}}] = 0$ | (7) |
流体体积函数F=F(x, y, z, t)代表计算区域内流体的体积占计算区域的相对比例。F=1,表示该单元完全被流体充满;F=0,表示该单元完全被气体充满;0<F<1,表示该单元包含气体和流体,有自由面。
2 有三角形障碍物的决口水流数值模型算例模拟验证 2.1 数值模型算例的建立为模拟验证决口水流遇障碍物的洪水演进过程,选取文献[16]中有三角形障碍物的溃坝算例水位场进行验证。该模型是1个由玻璃壁面封闭的系统,尺寸5.6 m ×0.5 m。上游水库长2.39 m,水位0.111 m,下游从水库至河道的三角形障碍物间无水。障碍物为底长0.9 m,高0.065 m的对称三角形,边坡0.14。障碍物下游有1个长0.7 m、深0.025 m的湖,如图 1所示。模型尺寸5.6 m×0.5 m×0.111 m,从精度考虑,将模型划分成0.02 m×0.02 m×0.01 m的单元。设置上游水库和下游湖的初始水位分别为0.111和0.025 m。求解设置:求解时间设为20 s,时间步长设为0.01 s。

|
图 1 试验模型平面布置及模型初始水位(单位:m) Figure 1 Plan layout of experimental model and its initial water level (unit: m) |
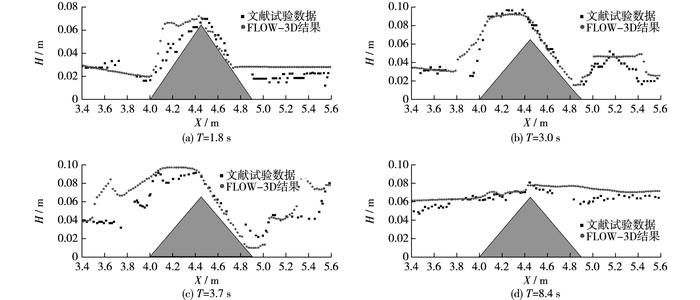
FLOW-3D计算结果与文献[16]试验数据在T为1.8,3.0, 3.7, 8.4 s时的水位对比见图 2,在T=1.8 s时,水流刚漫过三角形障碍物顶部向下游流动,但部分水流波被反射成负波传向上游(图 2(a));在T=3.0 s时,水流到达下游水池后,前波速度突然减慢,形成一个正波,如图 2(b),此时前波位置大致为5.2 m;在T=3.7 s时,波在下游墙处发生反射,若能量足够则可通过障碍物后向上游传播,如图 2(c)。水流经多次反射,在T=8.4 s后水位最终趋于稳定,如图 2(d)。模拟计算的各时刻水位变化规律与文献[16]中试验数据基本吻合,且符合水流运动规律,表明所建数值模型可以很好地重现非恒定流现象,验证了该模型的可靠性以及对决口封堵水流进行模拟的可行性。
|
图 2 FLOW-3D水位计算结果和文献[16]试验数据对比 Figure 2 Comparison between calculated results from FLOW-3D and document [16] |
以某河流堤防决口水流模拟建模,分析不同封堵方法对堤防决口水流的水力学特性。模拟区域为长700 m,宽100 m(河底)的长直河道,模型高10 m,河道坡降0.3‰,河道糙率0.025,决口高度8 m,距离下游河道200 m,河道左岸堤防高10 m,堤顶宽4 m,两侧边坡分别为1:1.05和1:0.85[17],河道及堤防典型断面如图 3所示。边界条件:物理边界条件设重力加速度为-9.8 m/s2,上游设初始流量为800 m3/s,上游初始水位为7 m,下游为自由出流;模型顶部设1个标准大气压,模型底部和左右两侧皆设定为固壁边界。初始条件:给定河道初始水位为5 m。设置求解时间为600 s,时间步长为2 s。

|
图 3 河道与堤防横断面及其三维图(单位:m) Figure 3 Cross-sections of river and dike and their 3D diagram (unit:m) |
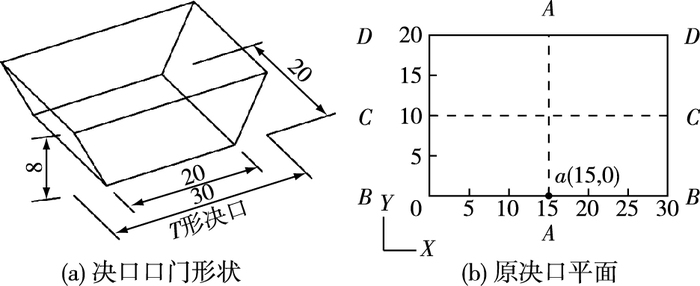
建立长直河道7 m水头下T形决口模型,模型顶部长20 m、宽30 m、高8 m,具体形状及尺寸如图 4所示。
|
图 4 决口口门形状及原决口平面(单位:m) Figure 4 Schematic diagram of levee breach (unit:m) |
分析原决口进口断面a(15, 0) 点水深及流速随时间的变化可知:在决口瞬间,水深迅速减小,流速迅速增大;随着决口断面流量的增加,a点水深逐渐增大,在200 s内,水位起伏变化,200 s后水位略有波动,直至T=403 s后基本达到稳定水位;a点流速在150 s前起伏增长,150 s后达到相对稳定状态,直至T=403 s后基本达到稳定流速,如图 5所示。

|
图 5 原决口a点水深和流速变化 Figure 5 Changes in water depths and velocities of point a of primary breach |
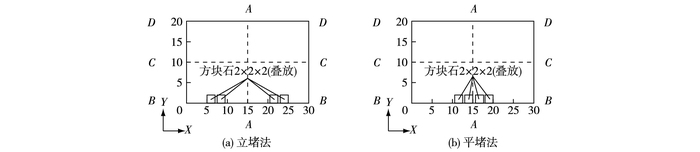
为计算方便,封堵材料选用8个2 m×2 m×2 m, 密度为1 800 kg/m3的方块石。立堵法方块石布置在决口进口断面、左右两侧叠两层放置,平堵法方块石布置在决口中轴线左右两侧叠两层放置,如图 6所示。
|
图 6 立堵法和平堵法决口平面(单位:m) Figure 6 Plan view of vertical and horizontal closure methods for dike breach (unit:m) |
FLOW-3D物理边界条件设置需激活运动模型,并对块石进行运动条件的设置,块石在初始时设为静止状态,在T=403 s时,下层块石开始向下运动,在其沉入决口底部后第2层块石开始运动。河道模型网格划分为2 m×2 m×1 m,决口出口50 m内平地网格加密为1 m×1 m×1 m,决口处因封堵料块石体积较小,为提高计算精度将决口处网格加密为0.5 m×0.5 m×0.5 m。
模拟过程中,当决口处水流趋于稳定后,选取图中所示决口处中轴线断面A-A、进口断面B-B、中部断面C-C、出口断面D-D在T=523 s时刻的结果进行封堵前后的堤防决口水力学特性对比分析。
3.2 水位场分布规律立堵封堵后的水深三维图与原决口相似,但在块石后面有2个明显漩涡;平堵后与原决口相比有部分变化,且在块石后面有1个明显漩涡;立堵和平堵封堵后的水面均有一定壅高。计算水深三维图见图 7。

|
图 7 决口水深三维图(单位:m) Figure 7 3D water depth hydrograph of dike breach (unit:m) |
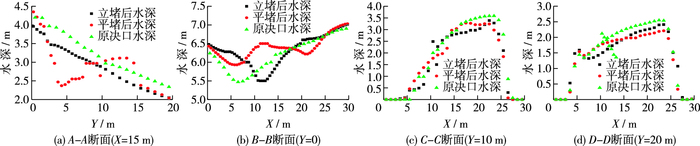
图 8(a)为决口中轴线断面A-A水深沿水流方向的分布,图 8(b)~(d)为决口B-B, C-C, D-D断面水面线沿决口宽度方向的分布。
|
图 8 各断面水深分布 Figure 8 Water depth hydrograph at different sections |
由图 8可见,立堵封堵后A-A断面与原决口平均水深变化规律基本一致,且低于原决口水深。平堵封堵后的水面线在沿水流方向上呈现先减后增而后再减小的变化规律。接近决口出口处立堵和平堵封堵后平均水深均低于封堵前平均水深。决口进口B-B断面封堵后块石前水位明显壅高。在X=6.50 m处,原决口最小水深5.47 m;在X=5.75 m处,立堵封堵后最小水深5.93 m;在X=11.75 m处,平堵封堵后最小水深为5.5 m。C-C, D-D断面封堵前后的平均水深在横向上的变化规律大致相似,其水面线在横向上呈两边低、中间及右侧偏高的不对称高拱形分布,总体来说,在断面左右两侧,封堵后平均水深要大于封堵前,但在断面中间部位,封堵后平均水深要小于封堵前。
3.3 流速场分布规律立堵封堵后的流速场分布和最大流速分布位置与原决口比较相似。平堵封堵后的流速场分布与原决口在块石后存在部分区别,但堤防上最大流速分布位置均在决口左侧。流速计算结果三维图如图 9所示。

|
图 9 决口三维流速(单位:m·s-1) Figure 9 3D velocities of dike breach by vertical and horizontal closure methods (unit:m·s-1) |
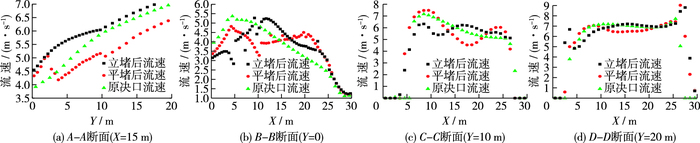
决口A-A, B-B, C-C, D-D等断面流速分布如图 10所示。立堵封堵前后A-A断面的平均流速沿水流方向的变化规律基本一致,且立堵封堵后该断面平均流速大于原决口及平堵封堵后的平均流速;平堵封堵后决口流速沿水流方向在堤防中轴线(Y=10.00 m)左侧起伏较大,在Y<3.50 m范围,平堵封堵后的平均流速比原决口大,在Y>3.50 m范围,平堵封堵后的平均流速比原决口小。
|
图 10 各断面流速分布 Figure 10 Velocity distributions at different sections |
对于B-B断面,在X=10.00 m左侧,立堵封堵后的流速比原决口小,右侧则比原决口大;立堵封堵后在X=9.00 m处达最大流速5.27 m/s,原决口、平堵封堵后均在X=4.50 m处达最大流速,分别为5.37和4.82 m/s。C-C, D-D断面上立堵、平堵封堵后和原决口平均流速在横向上均呈不对称拱形分布。对C-C断面,在X=8.50 m处,原决口最大平均流速7.16 m/s,立堵封堵最大平均流速6.32 m/s;在X=9.50 m处,平堵封堵最大平均流速7.48 m/s;对D-D断面,在X=26.50 m处,平堵封堵最大平均流速为9.03 m/s。
4 结语从数值模拟结果来看,无论立堵法还是平堵法,在封堵过程中,决口处的平均水深及流速都趋于均匀化,断面平均流速有所降低,有利于后续的封堵直至合龙;从施工难易程度上分析,平堵法适合单体大块石封堵,在合龙期(口门宽度较小)可采用;对于决口封堵的初期(宽口门),采用群体块石立堵法抛投更加快捷高效[18-19]。从决口流速分布看,该决口靠近水流上游侧流速较大,建议做好裹头处理,采取从决口口门水流下游侧沿堤防上堤脚线单边进占进行封堵,以避免左侧流速高而导致抛投块体被冲走。实际作业时,仍需根据决口现场实际情况合理制定封堵措施。
| [1] |
王运辉. 防汛抢险技术[M]. 武汉: 武汉水利电力大学出版社, 1999. ( WANG Yunhui. Flood control technology[M]. Wuhan: Wuhan University of Hydraulic and Electric Engineering Publishing House, 1999. (in Chinese))
|
| [2] |
刘铁奇, 高长权, 杨宏宇. 堤防决口的几项堵口技术[J]. 黑龙江水利科技, 2008, 36(4): 165. ( LIU Tieqi, GAO Changquan, YANG Hongyu. Several techniques for levee breach closure[J]. Heilongjiang Science and Technology of Water Conservancy, 2008, 36(4): 165. (in Chinese)) |
| [3] |
胡志根, 孟德乾, 黄天润, 等. 单戗堤立堵截流龙口的水力特性试验研究[J]. 水利学报, 2011, 42(4): 414-418. ( HU Zhigen, MENG Deqian, HUANG Tianrun, et al. Experimental study on hydraulic characteristics of gap in end-dumping closure with single embankment[J]. Journal of Hydraulic Engineering, 2011, 42(4): 414-418. (in Chinese)) |
| [4] |
宋利祥. 溃坝洪水数学模型及水动力学特性研究[D]. 武汉: 华中科技大学, 2012 (SONG Lixiang. Research on mathematical model and hydrodynamic characteristics of dam-break floods[D]. Wuhan: Huazhong University of Science and Technology, 2012. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10487-1012361474.htm
|
| [5] |
GARCIA R, KAHAWITA R A. Numerical solution of the St.Venant equations with the MacCormack finite-difference scheme[J]. International Journal for Numerical Methods in Fluids, 1986, 6(5): 259-274. DOI:10.1002/(ISSN)1097-0363 |
| [6] |
TORO E F. Riemann problems and the WAF method for solving the two-dimensional shallow water equations[J]. Physical Sciences and Engineering, 1992, 338(1649): 43-68. DOI:10.1098/rsta.1992.0002 |
| [7] |
魏文礼, 沈永明, 孙广才, 等. 二维溃坝洪水波演进的数值模拟[J]. 水利学报, 2003(9): 43-47. ( WEI Wenli, SHEN Yongming, SUN Guangcai, et al. Numerical simulation of 2D dam-break flood wave[J]. Journal of Hydraulic Engineering, 2003(9): 43-47. (in Chinese)) |
| [8] |
王志力, 耿艳芬, 金生. 具有复杂计算域和地形的二维浅水流动数值模拟[J]. 水利学报, 2005, 36(4): 439-444. ( WANG Zhili, GENG Yanfen, JIN Sheng. Numerical modeling of 2-D shallow water flow with complicated geometry and topography[J]. Journal of Hydraulic Engineering, 2005, 36(4): 439-444. (in Chinese)) |
| [9] |
岳志远, 曹志先, 李有为, 等. 基于非结构网格的非恒定浅水二维有限体积数学模型研究[J]. 水动力学研究与进展(A辑), 2011, 26(3): 359-367. ( YUE Zhiyuan, CAO Zhixian, LI Youwei, et al. Unstructured grid finite volume model for two-dimensional shallow water flows[J]. Chinese Journal of Hydrodynamics(SerA), 2011, 26(3): 359-367. (in Chinese)) |
| [10] |
冶运涛, 梁犁丽, 张光辉, 等. 基于修正控制方程的复杂边界溃坝水流数值模拟[J]. 水力发电学报, 2014, 33(5): 99-107. ( YE Yuntao, LIANG Lili, ZHANG Guanghui, et al. Numerical simulation of dam-break water flow with complex boundary based on governing equations modification[J]. Journal of Hydroelectric Engineering, 2014, 33(5): 99-107. (in Chinese)) |
| [11] |
曾秀娟. 堤防决口封堵水力学数值模型研究[D]. 南昌: 南昌大学, 2015 (ZENG Xiujuan. The study of dyke breach hydraulics numerical model closure[D]. Nanchang: Nanchang University, 2015. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10403-1015633236.htm
|
| [12] |
王月华, 包中进, 王斌. 基于Flow-3D软件的消能池三维水流数值模拟[J]. 武汉大学学报(工学版), 2012, 45(4): 454-457. ( WANG Yuehua, BAO Zhongjin, WANG Bin. Three-dimensional numerical simulation of flow in stilling basin based on Flow-3D[J]. Engineering Journal of Wuhan University, 2012, 45(4): 454-457. (in Chinese)) |
| [13] |
张健, 方杰, 范波芹. VOF方法理论与应用综述[J]. 水利水电科技进展, 2005, 25(2): 67-70. ( ZHANG Jian, FANG Jie, FAN Boqin. Advances in research of VOF method[J]. Advances in Science and Technology of Water Resources, 2005, 25(2): 67-70. (in Chinese)) |
| [14] |
张婷. 波浪的三维数值模拟及其应用[D]. 天津: 天津大学, 2009 (ZHANG Ting. Three-dimensional numerical simulation of waves and its application[D]. Tianjin: Tianjin University, 2009. (in Chinese))
|
| [15] |
王福军. 计算流体动力学分析[M]. 北京: 清华大学出版社, 2004. ( WANG Fujun. Computational fluid dynamics analysis[M]. Beijing: Tsinghua University Press, 2004. (in Chinese))
|
| [16] |
BISCARINI C, FRANCESCO S D, MANCIOLA P. CFD modelling approach for dam break flow studies[J]. Hydrology & Earth System Sciences, 2010, 14(4): 705-718. |
| [17] |
孙芦忠, 赵建均, 严建国, 等. 堤防决口的水力学试验研究[J]. 人民长江, 2003, 34(11): 41-42. ( SUN Luzhong, ZHAO Jianjun, YAN Jianguo, et al. Experimental study on hydraulics of dyke breach[J]. Yangtze River, 2003, 34(11): 41-42. DOI:10.3969/j.issn.1001-4179.2003.11.018 (in Chinese)) |
| [18] |
肖焕雄. 施工水力学[M]. 北京: 水利电力出版社, 1992. ( XIAO Huanxiong. Construction hydraulics[M]. Beijing: Water Conservancy and Electric Power Press, 1992. (in Chinese))
|
| [19] |
肖焕雄, 唐晓阳. 江河截流中混合粒径群体抛投石料稳定性研究[J]. 水利学报, 1994(3): 10-18. ( XIAO Huanxiong, TANG Xiaoyang. Stability of mixed riprap dumped for river closure[J]. Journal of Hydraulic Engineering, 1994(3): 10-18. (in Chinese)) |
2. No. 2 General Team of Armed Police Hydropower Troops, Nanchang 330096, China
 2017
2017 