2. 广西大学 工程防灾与结构安全教育部重点实验室,广西 南宁 530004;
3. 广西大学 广西防灾减灾与工程安全重点实验室,广西 南宁 530004
为了解降水结构变化特征,更好地避免降水变化带来的损失,国内学者对不同地区的降水特性做了很多深入的研究。王小玲等[1]对我国8个不同区域从不同强度年降水量、年降水频率和平均降水强度等角度分析了其趋势变化;邵晓梅等[2]借助小波分析探讨了黄河流域年降水在多时间尺度下的变化关系,并且分析了该变化结构的周期、突变点等;梅伟等[3]对长江中下游年和季的降水量、降水日数和降水强度进行分析,研究了其变化趋势和突变点,对不同等级的日降水量变化趋势进行了讨论。但国内学者大多从年、季、日降水的角度考虑,也大多停留在不同降水强度的分类方式,对于不同历时的降水事件在长时间序列中的特性没有更多的深入研究[4-5]。
广西南宁市处于亚热带季风气候区,为我国降水量最丰富地区之一,年均降雨量在1 300 mm左右。由于全球气候变化带来的降水变化以及降水分布不均匀,南宁市每年因洪涝灾害带来的经济损失逐年增加。
本文基于小波分析方法[6-7],针对不同历时降水事件的次数和降水量,研究降水在年时间序列上的多时间尺度的周期变化、变化强度等特征,为预测未来降水趋势提供依据。
1 资料与方法采用1971-2012年南宁市国家级地面气象站逐小时降水数据观测资料。根据资料发现4-9月的降水量占全年降水量的70%以上,因此选取4-9月的汛期降雨量来研究其降水结构变化特征。从降水历时出发,分析南宁市1~3 h,4~6 h,7~10 h,10 h以上4个历时降水的次数以及降水量的多尺度结构及变化趋势。
为了更准确地描述降水结构,对收集的原始数据进行距平处理[8],年降雨量序列和年降雨量平均值的差值及距平百分率的结果见图 1,可见,距平值较大年份主要出现在1986, 1989, 1994, 2001年。

|
图 1 降水量距平处理结果 Figure 1 Processing results of precipitation anomaly |
小波分析是由Morlet在20世纪80年代提出的基于Fourier变换的时频局部化分析方法[9]。小波分析采用的基本函数是复数小波Morlet小波,其定义为:
| $ \psi \left( t \right) = \exp \left( {i{w_0}t} \right)\exp \left( { - {t^2}/2} \right) $ | (1) |
且小波函数ψ(t)=L2(R)满足:
| $ \int_{ - \infty }^{ + \infty } {\psi \left( t \right){\rm{d}}t} = 0 $ | (2) |
同时,函数ψ(t)可构成一簇函数系:
| $ {\psi _{a, b}}\left( t \right) = {\left| a \right|^{ - 1/2}}\psi \left( {\frac{{t - b}}{a}} \right) $ | (3) |
对于信号f(t)∈L2(R),小波变化定义为:
| $ {W_f}\left( {a, b} \right) = {\left| a \right|^{ - 1/2}}\int_{ - \infty }^{ + \infty } {f\left( t \right)\bar \psi \left( {\frac{{t - b}}{a}} \right){\rm{d}}t} $ | (4) |
式中:Wf(a, b)为连续小波变换系数的二元函数,随参数a,b变化,代表小波变化系数;参数a为小波周期长度的尺度因子;参数b为时间平移的时间因子。小波变化系数图是关于Wf(a, b)的二维等值线图,反映了信号的时频变化特征。小波方差是对时间域上关于尺度因子的小波系数模的平方进行的积分:
| $ {\mathop{\rm var}} \left( a \right) = \int_{ - \infty }^{ + \infty } {{{\left| {{W_f}\left( {a, b} \right)} \right|}^2}{\rm{d}}b} $ | (5) |
小波方差图是方差var(a)随时间尺度的变化过程,代表了信号的显著周期。
Morlet小波变换的模可以代表时间尺度信号的强弱,实部则代表了不同时间尺度下的信号分布及相位等信息[10-11]。分别绘制实部和模平方的时频分布图,可以对降水序列进行多时间尺度分析,了解不同时间尺度的结构和变化趋势[12-13]。
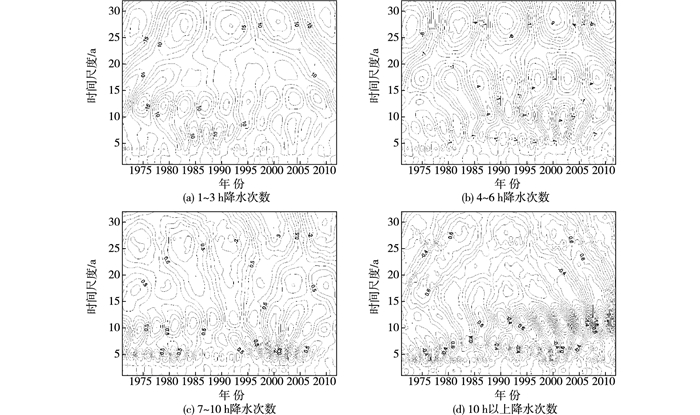
2 结果分析 2.1 各历时降水次数变化采用Morlet小波函数来分析南宁市各历时降水次数的多时间尺度演变规律,图 2为各历时降水次数序列小波系数实部时频变化。从图中信息可以得到,1~3 h降水次数在时间尺度5~9年, 10~15年, 23~29年, 周期变化较强,其中心时间尺度分别在4, 13, 28年左右。4~6 h降水次数在时间尺度3~12年, 15~20年, 22~31年变化较强,中心尺度分别在10, 17, 27年左右。7~10 h降水次数在时间尺度3~6年,7~14年,23~30年变化较强,中心尺度分别在5, 10, 26年左右。10 h降水次数在时间尺度2~9年, 10~15年, 25~30年变化较强,中心尺度分别在3, 11, 28年左右。
|
图 2 各历时降水次数小波系数实部时频分布 Figure 2 Time frequency distribution of real part of wavelet coefficients in duration of precipitation frequency |
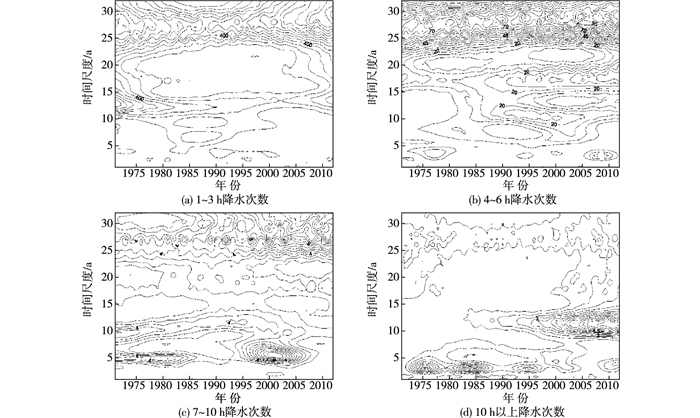
为进一步分析不同时段各时间尺度分布的强弱,绘制小波系数模平方时频分布如图 3。
|
图 3 各历时降水次数小波系数模平方时频分布 Figure 3 Time frequency distribution of wavelet coefficient modulus square in duration of precipitation frequency |
由图 3可见,1~3 h降水次数的22~30年时间尺度振荡较强,分布在整个时间序列;4~15年时间在1971-2002年有明显振荡,振荡中心在1987年左右;3~5年时间尺度也存在微弱变化。4~6 h降水次数的25~30年时间尺度变化较大,分布在整个时间序列;15~22年时间尺度在整个序列有振荡,中心在1982年、2002年左右;10~15年时间尺度在1983-2012年有微弱变化,中心在2004年。7~10 h降水次数的29~32年时间尺度振荡较强,分布在整个时间序列;4~7年时间尺度在1971-1993年有明显振荡,中心在1980年左右;3~9年时间尺度在1993-2010年有振荡,中心在2002年左右。10 h以上降水次数的9~15年时间尺度在1983-2012年振荡明显;2~7年时间尺度在1972-2006年振荡较明显,振荡中心分别在1976,1984,1995年左右;25~30年时间尺度有微弱振荡。
图 4给出了小波方差随时间尺度的变化过程,反映了小波能量在不同尺度下的变化规律。分析得知1~3 h降水次数变化过程的第1主周期为28年,第2主周期为13年;4~6 h的第1主周期为27年,第2主周期为17年;7~10 h的第1主周期为29年,第2主周期为5年;10 h以上的第1主周期为11年,第2主周期为3年。

|
图 4 各历时降水次数小波方差 Figure 4 Wavelet variance duration of precipitation frequency |
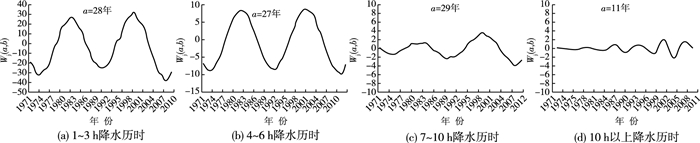
图 5给出了各历时降水次数的第一主周期的小波实部变换过程。其中,1~3 h降水次数存在2个高频期:1979-1987年、1996-2005年;3个低频期:1971-1978年、1988-1995年、2006-2012年。4~6 h降水次数存在2个高频期:1978-1986年、1996-2005年;3个低频期:1971-1977年、1987-1995年、2006-2012年。7~10 h降水次数存在2个高频期:1979-1985年、1996-2004年;3个低频期:1972-1978年、1986-1995年、2005-2012年。10 h以上降水次数在1971-1972年、1977-1980年、1985-1987年、1993-1996年、2001-2003年、2008-2011年为高频,其余时间均为低频。
|
图 5 主要时间尺度下各历时降水次数小波实部变换过程 Figure 5 Real part of wavelet transformation process of duration of precipitation frequency in main time scale |
可以看出主周期下6 h及以下的降水次数高低频交替变化十分明显,突变点分布也十分均匀,而6 h以上的降水次数高低频变化较弱,其中10 h以上变化非常微弱,但自1997年开始形成稳定交替趋势。可以预测,在未来2年内,各历时降水均将处于低频期。
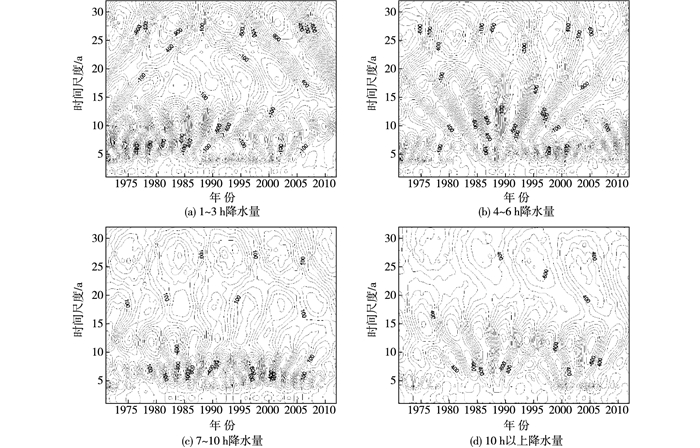
2.2 各历时降水量变化图 6为各历时降水量序列小波系数实部时频变化。分析可得,1~3 h降水量在时间尺度3~14年, 24~32年周期变化较强,其中心时间尺度分别在4, 7, 10, 28年左右。4~6 h降水量在时间尺度3~7年, 8~20年, 21~30年年变化较强,中心尺度分别在6, 12, 17, 26年左右。7~10 h降水量在时间尺度3~9年, 10~22年, 22~30年变化较强,中心尺度分别在6, 12, 18, 27年左右。10 h降水量在时间尺度3~6年, 7~20年, 22~32年变化较强,中心尺度分别在3, 12, 26年左右。
|
图 6 各历时降水量小波系数实部的时频分布 Figure 6 Time frequency distribution of real part of wavelet coefficients during precipitation |
绘制小波系数模平方时频分布如图 7。分析可得,1~3 h降水量的24~32年时间尺度振荡较强,分布在整个时间序列;5~12年时间在1971-2000年有明显振荡,振荡中心在1987年左右;2~4年时间尺度也存在微弱变化。4~6 h降水量的24~28年时间尺度变化较大,分布在整个时间序列;19~23年时间尺度在1971-1997年有振荡,中心在1982年左右;10~17年时间尺度在1990-2012年有变化,中心在2004年;2~5年时间尺度在多个时间段有微弱变化。7~10 h降水量的25~30年时间尺度振荡较强,分布在整个时间序列;5~10年时间尺度在1971-2010年有明显振荡,中心在1985,1991,2001年左右;14~16年时间尺度在1974-1991年有振荡,中心在1983年左右。10 h以上降水量8~17年时间尺度整个时间序列振荡明显;1~4年时间尺度在1972-1997年、1999-2011年振荡较明显,振荡中心分别在1976,1983,1993,2002年左右;25~30年时间尺度有微弱振荡。
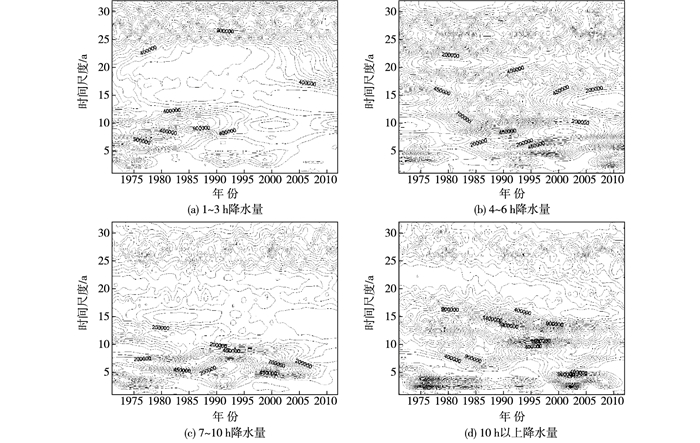
|
图 7 各历时降水量小波系数模平方时频分布 Figure 7 Frequency distribution of modulus square of wavelet coefficients in different durations of precipitation |
图 8给出了小波方差随时间尺度的变化过程,分析可得1~3 h降水量变化过程的第1主周期为28年,第2主周期为10年;4~6 h的第1主周期为26年,第2主周期为17或12年;7~10 h的第1主周期为29年,第2主周期为6年;10 h以上的第1主周期为12年,第2主周期为3年。

|
图 8 各历时降水量小波方差 Figure 8 Wavelet variance of different durations of precipitation |
图 9为各历时降水量第1主周期的小波实部变换过程。其中,1~3 h降水量存在2个丰水期:1979-1988年和1998-2006年;3个枯水期:1971-1978年、1989-1997年、2007-2012年。4~6 h降水量存在2个丰水期:1977-1985年和1994-2002年;3个枯水期:1971-1976年、1986-1993年、2003-2012年。7~10 h降水量存在3个丰水期:1971年、1980-1988年、1997-2005年;其余为枯水期。10 h以上降水量在1975-1978年、1984-1987年、1992-1995年、2000-2003年、2008-2011年为丰水期,其余时段均为枯水期。

|
图 9 主要时间尺度下各历时降水量小波实部变换过程 Figure 9 Process of real part of wavelet transform of different durations of precipitation in main time scale |
分析可得,除7~10 h降水量丰枯交替不明显,其他各历时降水量丰枯交替明显,突变点分布较为均匀。可预测未来2年内,除4~6 h外其他历时降水将处于枯水期。
3 结语(1) 通过小波分析,可得同一历时降水次数与降水量的时间尺度变化周期基本一致,其中降水量的周期变化更为明显,尤其是在10 h以上的长历时降水事件中,降水量的尺度周期变化明显大于降水次数。这意味着对于南宁市汛期降水特性的研究,降水事件的降水量变化更为显著,敏感度更高,研究意义也相对更大。
(2) 通过主周期的正负相位变化过程,可以看出在整个时间序列,10 h及以下历时降水次数的低频期明显长于高频期,10 h及以下历时降水量的枯水期明显长于丰水期;10 h以上历时的降水次数高、低频期相同,10 h以上历时降水量的丰、枯期十分接近。
(3) 根据预测可得未来2年内,4~6 h历时降水的降水量将处于丰水期,1~3 h,7~10 h,10 h及以上历时降水的次数及量都将处于低频期或枯水期。这对研究南宁市未来降水事件的结构变化提供了参考依据。
(4) 对于降水结构特性的研究,不仅要从降水历时考虑,而且应结合不同降水等级的降水事件予以更详细的分类研究,有助于更全面了解降水结构及变化趋势。
| [1] |
王小玲, 翟盘茂. 1957~2004年中国不同强度级别降水的变化趋势特征[J]. 热带气象学报, 2008, 24(5): 459-466. ( WANG Xiaoling, ZHAI Panmao. Changes in China's precipitation in various categories during 1957~2004[J]. Journal of Tropical Meteorology, 2008, 24(5): 459-466. (in Chinese)) |
| [2] |
邵晓梅, 许月卿, 严昌荣. 黄河流域降水序列变化的小波分析[J]. 北京大学学报(自然科学版), 2006, 42(4): 503-509. ( SHAO Xiaomei, XU Yueqing, YAN Changrong, et al. Wavelet analysis of rainfall variation in the Yellow River basin[J]. Journal of Beijing University(Natural Science), 2006, 42(4): 503-509. (in Chinese)) |
| [3] |
梅伟, 杨修群. 我国长江中下游地区降水变化趋势分析[J]. 南京大学学报(自然科学版), 2005, 41(6): 577-589. ( MEI Wei, YANG Xiuqun. Trends of precipitation variations in the mid-lower Yangtze River valley of China[J]. Journal of Nanjing University (Natural Science), 2005, 41(6): 577-589. (in Chinese)) |
| [4] |
宋晓猛, 张建云, 刘九夫, 等. 北京地区降水结构时空演变特征[J]. 水利学报, 2015, 46(5): 525-535. ( SONG Xiaomeng, ZHANG Jianyun, LIU Jiufu, et al. Spatial-temporal variation characteristics of precipitation pattern in Beijing[J]. Journal of Hydraulic Engineering, 2015, 46(5): 525-535. (in Chinese)) |
| [5] |
冶运涛, 梁犁丽, 龚家国, 等. 长江上游流域降水结构时空演变特性[J]. 水科学进展, 2014, 25(2): 164-171. ( YE Yuntao, LIANG Lili, GONG Jiaguo, et al. Spatial-temporal variability characteristics of precipitation structure across the upper Yangtze River basin, China[J]. Advances in Water Science, 2014, 25(2): 164-171. (in Chinese)) |
| [6] |
王文圣, 丁晶, 向红莲. 小波分析在水文学中的应用研究及展望[J]. 水科学进展, 2002, 13(4): 515-520. ( WANG Wensheng, DING Jing, XIANG Honglian. Application and prospect of wavelet analysis in hydrology[J]. Advances in Water Science, 2002, 13(4): 515-520. (in Chinese)) |
| [7] |
BOGGESS A. A first course in wavelets with Fourier analysis[M]. Hoboken: John Wiley & Sons, 2009: 4-10.
|
| [8] |
李芳, 林中达, 左瑞亭, 等. 基于经验正交函数和奇异值分解对东亚季风区跨季度夏季降水距平的订正方法[J]. 气候与环境研究, 2005, 10(3): 380-390. ( LI Fang, LIN Zhongda, ZUO Ruiting, et al. The methods for correcting the summer precipitation anomaly predicted extraseasonally over East Asian monsoon region based on EOF and SVD[J]. Climatic and Environmental Research, 2005, 10(3): 380-390. (in Chinese)) |
| [9] |
王文圣, 丁晶, 金菊良. 随机水文学[M]. 北京: 中国水利水电出版社, 2008. ( WANG Wensheng, DING Jing, JIN Juliang. Stochastic hydrology[M]. Beijing: China Water & Power Press, 2008. (in Chinese))
|
| [10] |
罗光坤. Morlet小波变换理论与应用研究及软件实现[D]. 南京: 南京航空航天大学, 2007. (LUO Guangkun. A study of morlet wavelet transform theory and application with software implementation[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2007. (in Chinese))
|
| [11] |
康玲, 杨正祥, 姜铁兵. 基于Morlet小波的丹江口水库入库流量周期性分析[J]. 计算机工程与科学, 2009, 31(11): 149-152. ( KANG Ling, YANG Zhengxiang, JIANG Tiebing. The periodical analysis of the Danjiangkou reservoir inflow based on the morlet wavelet[J]. Computer Engineering and Science, 2009, 31(11): 149-152. (in Chinese)) |
| [12] |
徐利岗, 周宏飞, 梁川, 等. 中国北方荒漠区降水多时间尺度变异性研究[J]. 水利学报, 2009, 40(8): 1002-1011. ( XU Ligang, ZHOU Hongfei, LIANG Chuan, et al. Multi-time scale variability of precipitation in the desert region of North China[J]. Journal of Hydraulic Engineering, 2009, 40(8): 1002-1011. (in Chinese)) |
| [13] |
张艳艳, 钟德钰, 吴保生. 黄河下游平滩流量驱动与响应模型[J]. 清华大学学报(自然科学版), 2012, 52(6): 759-765. ( ZHANG Yanyan, ZHONG Deyu, WU Baosheng. Response model for the bankfull discharge in the Lower Yellow River[J]. Journal of Tsinghua University(Science and Technology), 2012, 52(6): 759-765. (in Chinese)) |
2. Key Laboratory of Disaster Prevention and Structural Safety of Ministry of Education, Guangxi University, Nanning 530004, China;
3. Guangxi Key Laboratory of Disaster Prevention and Engineering Safety, Guangxi University, Nanning 530004, China
 2017
2017 
