天然河道总是处在不断地冲淤变化过程中，水流冲刷河床，使河床变形，河床的变形又促使水流结构发生变化。在河流上修建水工建筑物，对河床演变将会产生较大影响。而丁坝作为水工建筑物广泛应用于航道整治及护岸工程中，由于它改变了原有的河床过水断面形态，引起周围水流结构改变，并导致河床重新调整。

早在20世纪50年代初，国外已经开始对丁坝绕流问题进行了理论和试验研究^[1]。近年来，随试验手段和仪器设备的不断发展和更新，众多学者利用水槽及河工模型对丁坝展开了试验研究。Jennifer等^[2]通过水槽试验分析了丁坝附近流态紊动猝发特性。陈国祥等^[3]在水槽中进行了丁坝壅水试验，发现丁坝上游最大壅水断面的平均水位壅高值随流量压缩比和弗劳德数的增大而增大。陆永军等^[4]利用水槽试验结果，根据丁坝近区段流速分布呈自相似性对恢复区近段的流场进行了分析计算，推导出恢复区近段的流速分布式。应强等^[5]利用水槽试验对淹没丁坝附近的水流现象进行了定性描述，并导出淹没丁坝下游主流区流速变化公式。张华庆等^[6]利用水槽试验发现靠近丁坝侧区域横向流速较小，且表层横向流速大于底层；而随着与丁坝距离的增加，下游横向流速有所增大，且底层横向流速逐渐大于表层。Kuhnle等^[7]在水槽中采用Doppler流速仪测量了淹没梯型丁坝周围流速分布，结果显示在丁坝侧，底层纵向流速经过丁坝后明显减小，且在坝头处出现逆向的分离区；表层纵向流速近丁坝时减小，过坝顶时增加，过坝顶后再减小。黑鹏飞^[8]在矩形水槽中采用3D-PDA技术测量了丁坝下游水流的时均流场，并对其进行分区分析，发现丁坝下游不同流区纵向流速的垂向梯度均有所减小，但随着与丁坝距离的增加，流态逐渐恢复到无丁坝状态。李志勤等^[9-10]通过水槽试验和数值模拟对淹没丁坝绕流的水力特性进行了研究，发现在丁坝上游，水位自丁坝侧向对岸减小，且距丁坝一定距离的上游自由水面沿水流方向的纵向坡降较小。周宜林^[11]结合水槽试验和大涡数值模拟研究了上挑、正挑和下挑3种淹没丁坝近区水流特性，发现自附着点开始往下游丁坝一侧的水流流速逐渐增大。于守兵^[12]结合水槽试验和三维数学模型，研究了淹没丁坝对水流结构的调整作用，发现坝顶以上和坝头附近的横向流速随着淹没程度△H/H的增加而减小，并推导出横向水流影响范围与△H/H的经验关系式。李冰冻等^[13]利用水槽试验和数值模拟技术对淹没单丁坝附近的水位和流速进行了研究分析，发现丁坝对水流的影响集中在丁坝上下游一个较小区域，且横向上存在水力坡度。这些研究成果都是针对单一床面结构研究丁坝引起附近水流结构的改变情况，因此，本文利用水槽试验分析不同水力坡度情况下淹没单丁坝对近区水流结构的影响。

将淹没单丁坝作为研究对象，在一定流量下，通过改变水槽坡度，将丁坝近区水流结构的变化情况作为研究重点。试验物理模型主要由试验水槽、流量控制系统、自动水位测量系统及流速测量系统组成。试验在上海海洋大学水动力学试验室U形水槽中进行，水槽直道段长6.00 m，宽0.45 m，高0.55 m，测量段底板及侧壁均为钢化玻璃，试验水槽见示意图 1。丁坝模型长、宽10 cm，高20 cm，材料为普通玻璃，紧贴水槽边壁置于直道中段。试验流量为50 m³/h，尾门控制水深为30 cm，单丁坝为完全淹没状态。

图 1(Figure 1)

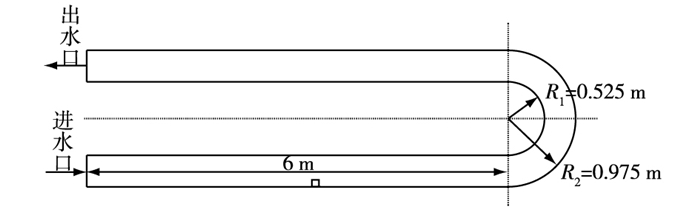
图 1 试验水槽 Figure 1 Schematic diagram of experimental flume

试验过程中进水流量、丁坝位置与尾门水位始终保持不变，通过调节变坡器依次改变水槽坡度为-1‰，0，1‰和2‰，(相应工况为1，2，3，4)。

水位测量采用超声波测量技术，测量系统主要由多个高精度超声水位探头、移动测车、水位采集综合控制箱以及自动水位测量软件等组成。在移动测车上，固定两个超声探头(两超声探头距离须大于25 cm，否则信号会有干扰)，丁坝对岸侧超声探头距离水槽边壁10 cm，丁坝侧超声探头距离边壁5 cm，在丁坝前、后共70 cm范围内设置9个水位观测断面，相邻两观测断面相距10 cm。各断面水位观测点布置见图 2(下列图表中沿程水位按从上游到下游1~9序号编排)。

图 2(Figure 2)

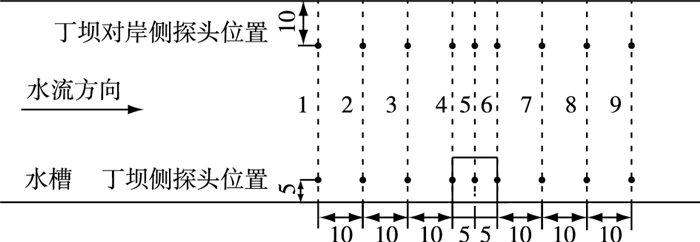
图 2 水位观测点布置(单位：cm) Figure 2 Layout of water level observation points (unit: cm)

流速测量采用PIV技术。由于激光宽度及相机的拍摄范围有限，因此，共设置了2个水平剖面的测量区域，拍摄剖面距离水槽底部10和25 cm，流速测量区域及观测点设置情况如图 3，其中，纵向观测点流速和横向观测点流速各7个，下列图表中纵向观测点流速按从上游到下游1~7序号编排，横向观测点流速按从丁坝对岸一侧到丁坝一侧1~7序号编排。

图 3(Figure 3)

图 3 流速测量区域及观测点布置(单位：cm) Figure 3 Layout of flow velocity measurement areas and observation points (unit: cm)

试验开始前，首先对每个水位测量断面的两个测量点进行水位零点标定。测量水位时，每个断面每次采集水位数据2 min，每个点大约有2 000多个水位数据，然后求平圴，作为测量点的水位值。

图 4为在不同水槽坡度条件下各观测断面水位沿程变化情况。从图中可以看出，在淹没丁坝的影响下，丁坝上下游水面线呈“凹”形，且随着水槽坡度的增大，同一断面的水位相应降低，“凹”形形状趋于扁平。在丁坝上游，当水槽坡度为负时，断面1处水位最高，当水槽坡度为正时，断面2处水位最高；在丁坝下游，除水槽坡度为2‰时断面9两点测量有误差外，其余各不同水槽坡度水位最高点都在断面9处。当水流流经丁坝后，丁坝中线断面至丁坝下游10 cm断面7处水位最低，且该段水位沿程变化非常小，水面线接近于水平。

图 4(Figure 4)

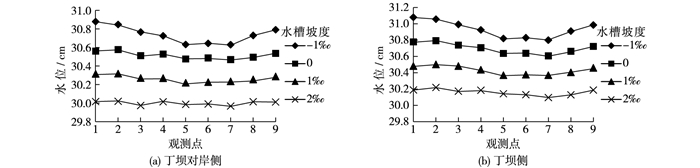
图 4 不同水槽坡度下沿程水位变化 Figure 4 Changes of water level under different flume slopes

表 1是不同水槽坡度下淹没丁坝上下游水面比降变化，从表中可以看出，丁坝上游水面比降为正，表明沿程水位逐渐减小，流速越来越大；丁坝下游水面比降为负，表明沿程水位逐渐增大，流速越来越小。且丁坝上下游水面比降随水槽坡度的增加逐渐减小，说明丁坝引起的水位变化范围在逐渐缩小，即随着水槽坡度增大，丁坝上游最高水位位置向下移动，而丁坝下游水位恢复点的位置则向上移动。当水槽坡度为负时，上下游水面比降比水槽坡度为正时大许多，说明负比降时淹没丁坝对水流的影响范围更大。从整个测量段水槽各断面水位变化情况来看，丁坝一侧的上下游水面比降比丁坝对岸的上下游水面比降要大许多，说明丁坝一侧上游出现了壅水、丁坝下游水位则有明显的跌落后再迅速上升的现象。

表 1(Table 1)

表 1 不同水槽坡度淹没丁坝上下游水面比降测量值 Table 1 Measured values of water surface gradient in vicinity of submerged dike under different flume slopes 水槽坡度/‰ 不同位置水面比降/‰ 丁坝对岸侧 丁坝侧 -1 8.204/-8.119 8.670/-9.320 0 3.356/-3.379 5.232/-5.800 1 3.290/-2.608 4.415/-4.509 2 1.080/-2.208 2.560/-3.388 注：“/”前为上游水面比降，“/”后为下游水面比降。

表 1 不同水槽坡度淹没丁坝上下游水面比降测量值 Table 1 Measured values of water surface gradient in vicinity of submerged dike under different flume slopes

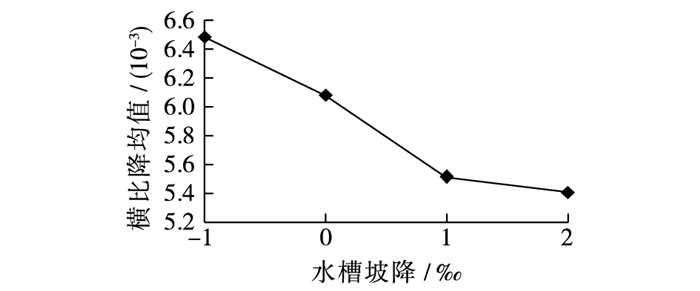
图 5为不同水槽坡度下沿程横比降变化情况，从图可见，同一水槽坡度在丁坝上游断面3处横比降最大，说明丁坝前壅水明显，在丁坝下游断面7处，横比降最小(2‰水槽坡度时测量上有误差)，说明水流经过丁坝后跌水明显。在丁坝上游，横比降沿程逐渐增大，且水槽坡度为0时，横比降最大，在断面3处最大值为7.57‰。在丁坝下游，横比降变化与水槽坡度存在对应关系，即随着水槽坡度的增大，横比降逐渐下降；而横比降沿程变化是先减小至断面7后再逐渐增大，说明水流经过丁坝跌水后回升迅速。在水槽坡度为-1‰时，横比降较其他水槽坡度时大许多，说明负水槽坡度时，因一部分动能转化为势能，水流流速较小，水流经丁坝后，跌水也较小。图 6为不同水槽坡度横比降均值变化情况，可见，在淹没丁坝影响范围，横比降随着水槽坡度的增加逐渐下降，即水槽坡度越大，横向水位差越小，说明流速越大，丁坝的壅水作用会越弱。

图 5(Figure 5)

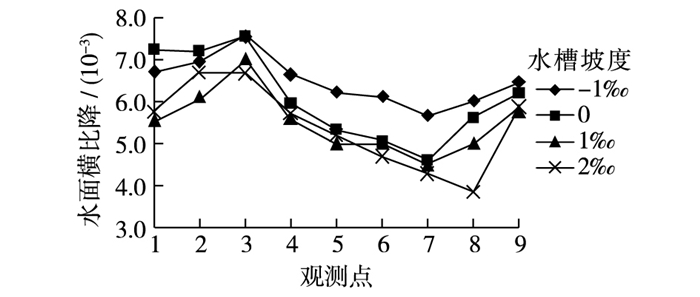
图 5 不同水槽坡度沿程水面横比降变化 Figure 5 Longitudinal changes of water surface transverse gradient under different flume slopes

图 6(Figure 6)

图 6 横比降均值与水槽坡度的关系 Figure 6 Relationship between averaged water surface transverse gradient and flume slope

表 2为不同水槽坡度淹没丁坝水流特征参数变化情况；△H为坝顶到自由水面的距离，H为丁坝处平均水深，△H/H为淹没程度，△H/H越大，表明坝顶溢流作用越大。从表中可以看出，随着水槽坡度的增加，△H/H变小，丁坝迎水面与背水面的水位差也减小。尽管水槽坡度为-1‰时，水槽水流平均流速较小，但丁坝迎水面与背水面的水位差较大，且弗劳德数也最大，即水流的惯性力最大，说明水槽坡度从-1‰增加到1‰时，丁坝的溢流作用随△H/H的变小而减弱。但当水槽坡度为2‰时，尽管丁坝迎水面与背水面的水位差最小，但弗劳德数却最大，水流惯性力较大。因此，用△H/H的变化分析淹没丁坝坝顶溢流作用的变化，应考虑引入其他参考因子。

表 2(Table 2)

表 2 淹没丁坝水流特征参数 Table 2 Characteristic parameters of submerged spur dike 水槽坡度/‰ △H/H 丁坝两侧水位差/mm 弗劳德数 -1 0.351 1.925 0.060 0 0.347 1.320 0.054 1 0.341 1.121 0.059 2 0.337 0.782 0.065

表 2 淹没丁坝水流特征参数 Table 2 Characteristic parameters of submerged spur dike

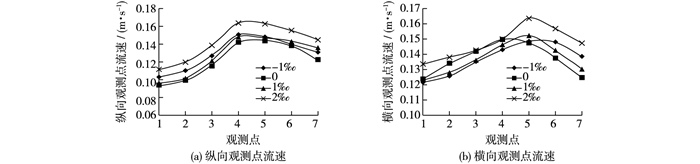
利用PIV系统分别测量距水槽底10和25 cm处的水平剖面的流速场。在10 cm处，由于丁坝附近及丁坝后水流存在较强紊动，每个测量区分别拍摄200张流场图像，然后求平均；在25 cm处，即丁坝顶上方5 cm处，水流紊动较10 cm处弱，每个测量区分别拍摄50张流场图像，然后求平均。图 7为距水槽底部25 cm处各观测点的流速分布。

图 7(Figure 7)

图 7 不同水槽坡度距水槽底25 cm处观测点流速沿程分布 Figure 7 Flow velocity distributions at observation points with 25 cm distance from flume bottom under different slopes

由图 7可见，在纵向上，最大流速都出现在丁坝上方，最小流速出现在丁坝前最远点；当水槽坡度为-1‰时，纵向观测点的流速及最大流速都较水槽坡度为0和1‰时流速大(见图 7(a))，由表 1可以发现，水槽坡度为负时水面比降最大；当水槽坡度从0变化到2‰时，纵向观测点的流速随水槽坡度的增加而增加，水面比降随水槽坡度的增加却有所减小，说明势能转变为动能是流速增加的主要因素，且水槽坡度为2‰时，平均流速和最大流速增加较大，增加幅度都超过10.0%。在横向上，横向观测点的流速随水槽坡度的增加而增加(见图 7(b))，最大流速出现在坝头前10 cm左右处，最小流速出现在丁坝对岸一侧最远点；当水槽坡度小于2‰时，横向观测点的平均流速基本相等，最大流速增幅也较小，小于1.5%，说明当水槽坡度小于2‰时，淹没丁坝对丁坝上方5 cm处的剖面水流影响较小；当水槽坡度为2‰时，横向观测点的平均流速及最大流速增加较大，增加幅度超过7.0%。结合纵向流速观测点平均流速及最大流速变化程度分析，可以认为，在水槽坡度为1‰和2‰之间，淹没丁坝对水流结构的影响可能存在一个临界变化点。

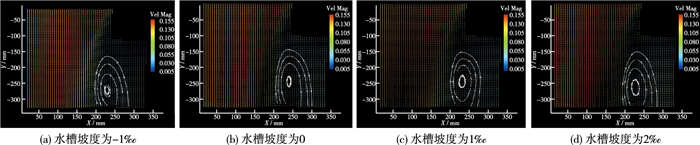
图 8为距水槽底部10 cm处各水槽坡度丁坝处剖面流场。从图 8可见，各水槽坡度在坝后产生了漩涡，漩涡流速分布较为相似，并在坝后出现了负流速区，但漩涡中心位置略有些变化。表 3为不同水槽坡度漩涡中心移动情况，当水槽坡度为-1‰时，丁坝下游漩涡中心距丁坝最远，为15.7 cm，离丁坝一侧边壁的距离为11.5 cm；当水槽坡度为0时，丁坝下游漩涡中心距丁坝及距丁坝一侧边壁最近，分别为13.2和10.8 cm。

图 8(Figure 8)

图 8 不同水槽坡度距水槽底10 cm处水平剖面流场 Figure 8 Flow fields at horizontal plane with 10 cm distance from flume bottom under different flume slopes

表 3(Table 3)

表 3 不同水槽坡度距水槽底10 cm处漩涡中心位置 Table 3 Vortex center positions at plane with 10 cm distance from flume bottom under different flume slopes 水槽坡度/‰ 与丁坝距离/ cm 与丁坝侧边壁距离/ cm -1 15.7 11.5 0 13.2 10.8 1 13.4 11.3 2 14.8 11.7

表 3 不同水槽坡度距水槽底10 cm处漩涡中心位置 Table 3 Vortex center positions at plane with 10 cm distance from flume bottom under different flume slopes

当水槽坡度从0变到2‰时，丁坝下游漩涡中心向下游移动同时，也向丁坝对岸一侧移动，坝后负流速区流速也相应增大(见表 4)，即漩涡强度逐渐增大，最大负流速靠近边壁；横向平均流速及最大流速则随水槽坡度的增加而增大，最大流速在丁坝对岸第2个观测点上。表 4还说明在正流速区，水槽坡度为-1‰时的流速比其他水槽坡度时的流速小，而在负流速区，水槽坡度为-1‰时的流速与水槽坡度为1‰时的流速很接近，显然，由于水力坡度的差异，坝后会产生更为复杂的水流结构形态。

表 4(Table 4)

表 4 不同水槽坡度距水槽底10 cm处沿漩涡中心横向观测点流速 Table 4 Flow velocity of observation points along vortex center transversal line with 10 cm distance from flume bottom under different flume slopes (m·s-1) 水槽坡度/‰ 横向各观测点流速 平均流速 1 2 3 4 5 6 7 -1 0.148 0.151 0.136 0.060 -0.002 -0.032 -0.044 0.059 0 0.149 0.154 0.148 0.079 -0.002 -0.026 -0.036 0.066 1 0.152 0.156 0.147 0.074 -0.002 -0.030 -0.048 0.065 2 0.153 0.157 0.147 0.073 -0.002 -0.041 -0.052 0.062

表 4 不同水槽坡度距水槽底10 cm处沿漩涡中心横向观测点流速 Table 4 Flow velocity of observation points along vortex center transversal line with 10 cm distance from flume bottom under different flume slopes

通过试验研究，分析了不同水力坡度下淹没单丁坝近区水流结构。试验结果表明，水力坡度不同，丁坝附近的水位、横比降、淹没程度△H/H、坝后漩涡中心位置、丁坝上游最高水位及下游水位恢复点位置、丁坝附近的流速变化等各种水力要素都表现不同，说明了淹没丁坝水流结构的复杂性。而天然河道的床面构造及水流结构比本试验情况还要复杂得多，因此，研究结果有助于深入探讨河床演变及海岸工程等复杂水动力问题。

GU Jie, ZHENG Yuhua