随着现代水利技术的发展和水资源的开发利用,我国已成为世界上大型水库拥有量最多的国家。与小型水库不同,大型水库由于水深和库容较大,极易形成水温垂向分层现象,对库区及下游生态环境带来系列不利影响。由于气象条件和水动力条件综合作用,水温分层现象在春末夏初尤为明显。在气象方面,春夏两季水库表层水体温度快速升高,密度随之降低,抑制水体的垂向混合,导致温度分层现象;在秋冬季节,由于热量的损失使得表层水体密度增大,水体垂向混合作用加剧,温度分层现象减弱。在水动力方面,春夏季节,与库内水体相比,上游来水温度较高、密度较小,会浮于水库上层导致分层;在秋冬季节,由于来水温度较低,会进入水库底层水体和表层高温水体之间,水体在运动过程中会受到较大的摩擦阻力,引起剧烈的垂向混合,进一步降低温度分层出现几率。由于气象条件不可控,通过改变取水口位置或流量等水动力条件是防止或减弱春末夏初水温分层的主要措施。研究不同水动力条件对于水库温度分布特性的影响,具有重要的现实意义。
目前预测大型水库温度的主要方法有经验公式和数学模型两种方法。在数学模型研究方面,朱伯芳[1]和张大发[2]提出了用经验类比法来预测水库水温,然而由于在经验公式中难以全面考虑各种影响因素,预测精度不高。为了弥补经验类比法的不足,Orlob等[3-6]开发了一系列垂向一维模型,刘肖等[7-11]提出用二维模型预测垂向和纵向水温分布,丁正锋等[12-15]建立了三维水库水温模型来模拟大型水库的水温分层现象。目前数学模型面临的最大困难是计算所需资料要求极高,而大型水库水深较大不易测量难以满足其模型验证和参数率定的要求,极大地影响了模型的应用。
物理模型是模拟自然现象最为直观的方法,可避免现场观测因时空布置和人员设备调配等因素的限制,是工程实际中应用最广的研究手段,而且可为经验公式法和数学模型的验证和参数率定提供有效的数据支持。华祖林[16]和王鳌然[17]采用物理模型研究温度分层流,但研究主要集中于温度垂向分布对水力参数的影响以及取水口位置和下泄温度之间的关系。目前,对于温度分层的形成和演化过程的物理模型模拟尚未见报道。
根据春末夏初水库库首(即水库内靠近大坝水流较为平缓的区域)水温分层流动特性,建立水槽水温分层流动的模拟试验系统,观测水温分层条件下温度沿程变化和垂向结构变化,分析测量断面、取水口高程和进水流量对水温垂向结构和下泄水温的影响,为制订水库调度措施提供参考。
1 试验方案与过程 1.1 试验系统设计与主要测量设备由于大型水库库首段流速较小,纵向水深变化较小,物理模型将其概化为顺直试验水槽,上游进口设置为表层进水,模拟春夏之交水库的上游高温来水,下游设置不同出水口,模拟不同的水流下泄方式。
图 1为试验系统示意图,包括水槽、装有加热器的水箱、泵等装置。为了更好地观测,试验水槽采用透明有机玻璃制成,设计尺寸:水槽宽0.5 m,高0.6 m,总长4 m,剖面及平面如图 2所示。在下游末端设计了2个直径3 cm的取水口,分别位于底部以上3.5和33.5 cm处。进水口位于上游,高程与水库水体水位一致。通过调节图 1中上下游阀门可对流量进行控制。

|
图 1 试验系统示意 Figure 1 Schematic diagram of experimental system |

|
图 2 大型水库库首试验水槽 Figure 2 Experimental flume for a large reservoir |
温度测量采用厦门宇电自动化科技有限公司生产的AI-5600型手持式高精度数字温度计逐点测量,温度计最高分辨率为0.001 ℃,测量精度为±0.06 ℃,探头直径为2 mm,测量过程中忽略探头对于流场的扰动影响。
1.2 试验工况及过程 1.2.1 试验工况为了研究不同进水流量和多种取水方式下温度的沿程变化和垂向结构变化,结合试验条件,确定了4种试验工况,具体如表 1所示。
| 表 1 物理模型试验工况 Table 1 Working conditions for physical model tests |
为了测量水温在沿程和垂向分布上的变化,分别在水槽中距离上游进水口50 cm和下游出水口50 cm处设置了两个监测断面,在每个检测断面上垂向设置5个监测点,分别位于水槽底部以上5,10,20,30和35 cm处。所有监测点均分布在水槽中心线的剖面上,距离水槽两侧25 cm。密度弗劳德数Fr的定义为:
| $ Fr = {u_0}/\left( {\sqrt {\frac{{{\rho _{\rm{c}}} - {\rho _{\rm{h}}}}}{{{\rho _{\rm{c}}}}}} gD} \right) $ | (1) |
式中:ρc采用初始时刻水槽内水体密度;ρh为进水口注入的高温水密度;u0为水槽横截面的平均流速;D为水槽内水深。
1.2.3 试验过程模型试验过程如下:在水槽中注入24.5 ℃的自来水至35 cm水深,然后从水槽进水口注入36 ℃热水,同时根据工况设定的参数,调节进水口和取水口阀门,使二者流量保持一致,控制水槽水深为35 cm。在试验过程中,记录各种工况下监测断面不同深度的水温变化,直至水槽内水温混合均匀为止。每种工况重复5遍,然后对5次相同试验的数据取平均值,以减小水流随机性所产生的误差。
2 结果与分析根据4种工况的试验结果进行分析,探究在不同流量和取水口高度条件下,水库沿程和垂向水温分布的变化规律。为了分析温度分层对于垂向紊动扩散强度的影响,计算了不同工况下的里查德森数,计算公式为
| $ Ri = {N^2}/{\left( {\frac{{\partial u}}{{\partial z}}} \right)^2} $ | (2) |
式中:N为浮力频率,
工况1条件下,上游监测断面的结果显示(见图 3(a)),试验刚开始时,垂向温度分布明显可分为两层,分别为上部的变温层和底部的均温层。当试验进行到第60 s时,来流温度对水槽内温度分布的影响主要表现在水深15 cm范围内。第120 s时,影响范围扩大到水深25 cm,且在变温层中间部分即水深5~15 cm段出现了明显的混合层,该层温度相对均匀,热量混合最为剧烈,第180 s时该混合层的垂向温度更加均匀,此时变温层的影响范围达到30 cm水深。第360 s时,均温层逐渐消失被变温层所取代。
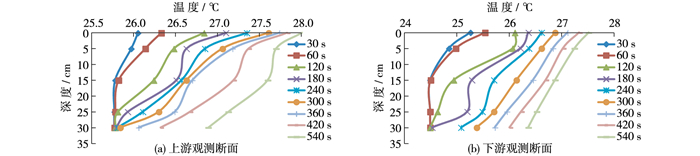
|
图 3 工况1条件下水温垂向分布随时间的变化 Figure 3 Vertical temperature distribution at different times of working condition 1 |
下游监测断面的结果显示(见图 3(b)),前60 s与上游断面分布相似,仅在表层存在变温层。第120 s时,由于水槽末端固壁的阻碍作用,改变了表层热水的流动方向,在水深0~5 cm处出现了混合层,并在其下方形成了两段温度梯度不同的变温层。随后混合层开始向下移动,第180 s时,出现在水深15~25 cm段,并形成了三段温度梯度不同的变温层,这主要是受到出水口垂向混合作用的影响。从第300 s开始,水温随着水深的增加而降低,温度的垂向分布结构不再随时间而改变。在这种工况下,研究时段内水槽内的理查德森数Ri介于82.8~563.0,温度分层对垂向扩散的抑制作用较强。
如图 4所示,与工况1相比,由于流量较大,工况2中上下游监测断面受来流温度影响更加明显,变温层范围在试验开始阶段就达到了25 cm水深。随着试验的进行,在中间段出现混合层,出现位置与工况1大致相同,但工况2的混合层没有工况1明显。由于工况2出水流量增大,中间段的混合层对下游的影响变得显著,在300 s时,混合层的影响水深范围为5~25 cm。在这种工况下,研究时段内水槽内的理查德森数Ri介于14.3~95.0,温度分层对垂向扩散的抑制作用弱于工况1。

|
图 4 工况2条件下水温垂向分布随时间的变化 Figure 4 Vertical temperature distribution at different times of working condition 2 |
如图 5所示,与工况1和2相比,工况3在试验前60 s,表层温度变化较为强烈,变温层的温度梯度较大。第240 s时,上游监测断面出现混合层,且在其上下方各有一个变温层,之后混合层逐渐消失,被变温层所取代。下游监测断面在试验开始阶段温度分布结构与上游监测断面相似,但300 s后垂向温度分布变得更加复杂,如第420 s时,断面交替出现两个混合层和变温层。在这种工况下,研究时段内水槽内的理查德森数Ri介于353.1~914.1,温度分层对垂向扩散的抑制作用非常强。
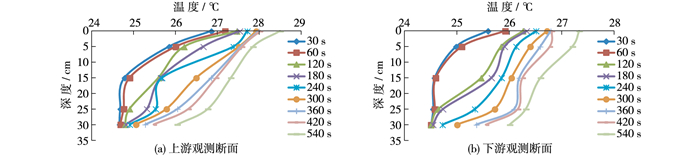
|
图 5 工况3条件下水温垂向分布随时间的变化 Figure 5 Vertical temperature distribution at different times of working condition 3 |
如图 6所示,与工况3相比,工况4的温度分层现象更为明显。上游监测断面,第30 s时,在0~5 cm水深处出现了混合层,第60 s时,热水到达下游出口,混合层消失。第60 s以后,温度垂向分布由三段变温层组成,其中位于表层和水槽底部的两个变温层温度梯度较大,中间段的温度梯度较小。下游监测断面,在前60 s时,0~15 cm水深处为变温层,其下方为均温层。第120 s时,在0~5 cm水深处出现了混合层,由于受到来流温度的显著影响,混合层消失,水温随着水深的增加而降低,温度的垂向分布结构不再随时间而改变。在这种工况下,研究时段内水槽内的理查德森数Ri介于28.9~106.3,温度分层对垂向扩散的抑制作用强于工况2,但弱于其他3种工况。
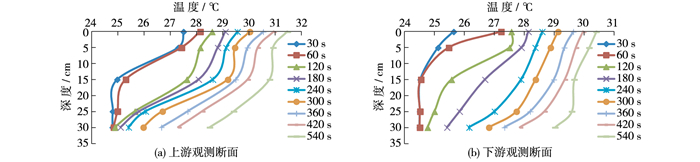
|
图 6 工况4条件下水温垂向分布随时间的变化 Figure 6 Vertical temperature distribution at different times of working condition 4 |
从图 7可知,上游断面的分层现象比下游断面更为明显,这是沿程不断进行的垂向混合运动造成的。由于试验开始阶段进入的热水较少,分层现象并不明显,随着热水不断注入,分层现象也愈发明显。随着温度较低的水体不断排出水槽,分层现象逐渐消失。

|
图 7 垂向温差随时间变化的比较 Figure 7 Changes of vertical temperature with time |
水槽上游的热水流量对于温度分层具有明显影响。在同一取水口条件下,比较工况3和工况4可以发现,上游监测断面最大垂向温差从2.87 ℃升高至4.15 ℃,随着流量的增加水槽内温度分层也更加强烈。
取水口的高度同样会影响水槽内温度分布。在同一进水流量条件下,比较工况2和工况4可以发现,上游监测断面最大垂向温差从3.56 ℃升高至4.15 ℃,取水口位置较高时,温度分层现象更为明显。
因此,通过加大进水流量和降低取水口的高度,可以有效抑制水库中温度分层现象的产生。通过科学的水库调度方式可以削弱水温分层对生态环境的不利影响。
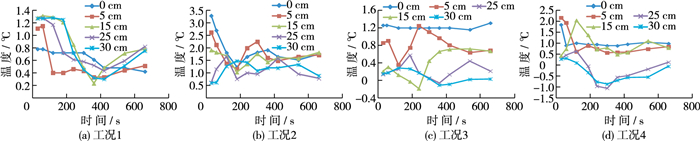
2.3 上下游温差随时间的变化图 8为不同水深条件下,上下游监测断面温差监测时段内随时间的变化。下面分别按表层、中间层和底层对4种工况的温度变化进行分析。
|
图 8 不同深度上下游断面温差随时间的变化 Figure 8 Time series changes of temperature difference between upper and lower sections |
比较工况1和2可知,同一水深下,上游断面温度总是高于下游断面,这是因为热水总是先经过上游断面,且上游断面垂向的混合程度也不如下游断面均匀。同时可以发现工况2的温差大于工况1,这是因为工况2的流量更大。
初始阶段,热水还未到达下游导致上下游表层温差较大。工况1的表层温差随时间的增加而减小,增大进水口流量后,工况2的表层温差变化更为复杂,在第180 s时出现了极小值。这是因为热水注入水槽表层后,向下游移动,下游温度也随之升高,表层温度处于减小过程。当上层水体流动至水槽末端时,受到固壁的影响,水温在垂向的混合加剧,表层热量传递到深处,下游监测断面表层温度降低,上下游表层温差再次处于上升过程。
比较工况3和4可知,当下游取水口位于水槽表层时,上游断面温度总是高于下游断面,表层温差随时间变化幅度不大,但随着进水口流量的增加,温差会相应增加。
2.3.2 中间层温差变化比较工况1和2可知,中间层上游断面温度高于下游断面,工况2由于流量较大,温差也较大。初始阶段温差较大,随后开始减小,达到极小值点后再次升高,这一现象与热水在水槽中的运动过程密不可分。初始时段,热水注入水槽时,上游断面快速升温,其影响还未波及下游,因此上下游会产生较大温差。随着热水移动到下游,以及底部取水口的作用,温度在垂向上的混合加剧,使下游中间段温度升高,上下游温差开始减小并达到极小值。此外,当下游垂向混合剧烈时,将会对整个断面的温度产生影响,导致中间层升温速度较慢,因此在温差达到极小值后再次缓慢增加。
工况3和4的中间层温差随时间的变化规律与工况1和2大体相同,只是在试验初始阶段,温差存在上升过程,这是取水口高度不同所致。工况1和2的取水口位于水槽底部,温度垂向混合剧烈,而工况3和4的取水口位于水槽表层,导致在开始阶段热水仅在表层水平方向移动,上下游中间层受热水影响较小,升温速度相对较慢,因此,试验开始阶段温度差会呈上升趋势。
2.3.3 底层温差变化与工况2的温差变化趋势不同,热水到达下游底部之前,工况1底层温差均保持在较高值。由于工况2出现了明显的温度分层,导致试验初始阶段水槽底部的水温较低,随着上游断面底部水体从取水口排出,底部水温不断升高,导致温差增大。
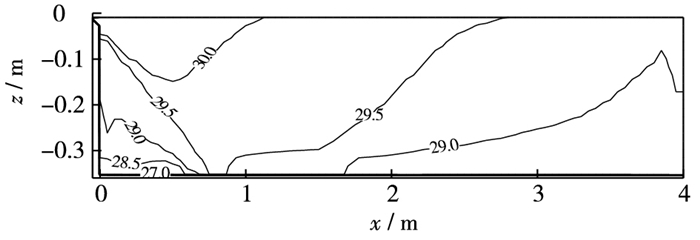
工况3和4底部温差分别小于工况1和2,且出现负值,表明上游底部水温低于下游底部水温。由于该工况条件下取水口位于水槽表层,水温分层现象明显,从而抑制了温度在垂向上的混合。由于温度分层现象在上游表现得更为明显,导致上游底部水温相比于下游上升速度较慢,上下游温差出现负值,这与文献[18]中数学模型计算结果一致(见图 9)。
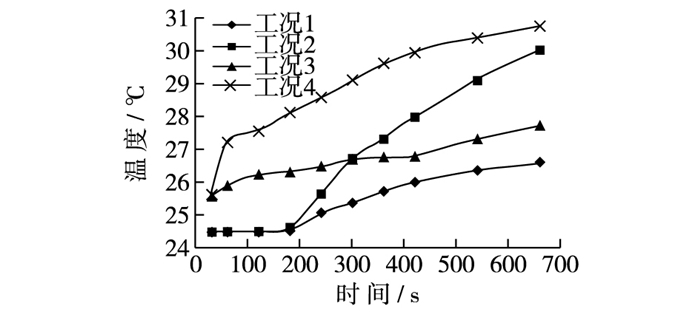
2.4 下游出水温度从图 10可知,取水口高度与进水口流量均会对出水温度产生影响。分别比较工况1,3和2,4,发现进水流量相同时,取水口位置越高出水温度越高,最大出水温差可达3.5 ℃。分别比较工况1,2和3,4,发现取水口位置相同时,进水流量越大出水温度越高,最大出水温差可达3 ℃。试验结果表明,通过改变取水口高度与进水口流量可以有效控制水库的出水温度,对保护水库下游水环境具有重要现实意义。
|
图 10 出水温度随时间变化 Figure 10 Time series of outlet temperature |
水库的合理设计和科学运作是减少水温分层负面作用的有效方式。通过物理模型试验,模拟研究了春末夏初库首段上游来水条件和下游取水条件对水温分布的影响,结论如下:① 随着上游来水进入库区,库首水温垂向结构可出现多种不同形式。初始阶段,垂向水温由变温层和均温层两层组成。随着时间的增加,水温垂向结构变得更为复杂,可能出现3个温度梯度不同的变温层,也有可能在两个变温层中间出现混合层。② 温度分层强度取决于水动力条件。上游温度分层现象比下游更为明显,这是由水流运动过程中的垂向混合作用所致。入口热水流量增大,取水口位置较高,都会导致水库水温分层强度增加。③ 同一深度水温的沿流分布具有明显规律性。当取水口位于底部时,同一深度的上游水温高于下游。当取水口位于表层时,由于上游出现明显的温度分层,导致上游底部水温低于下游。④ 出水温度很大程度受到进水流量和取水口高度的影响。入口热水流量增大,取水口位置升高,均会引起出水温度升高,试验工况下最大温差可达3.5 ℃。
由于水动力条件与边界条件对于温度分层流特性具有重要影响,本次试验工况尚不够全面,今后还需开展关于底坡和糙率等条件对于水温分层流动特性影响的物理试验。
| [1] |
朱伯芳. 库水温度估算[J]. 水利学报, 1985(2): 12-21. ( ZHU Bofang. Prediction of water temperature in reservoirs[J]. Journal of Hydraulic Engineering, 1985(2): 12-21. (in Chinese)) |
| [2] |
张大发. 水库水温分析及估算[J]. 水文, 1984(1): 19-27. ( ZHANG Dafa. Analysis and assessment of water temperature in reservoirs[J]. Hydrology, 1984(1): 19-27. (in Chinese)) |
| [3] |
ORLOB G T, SELNA L G. Temperature variation in deep reservoirs[J]. Journal of Hydraulics Division, ASCE, 1983, HY3(108): 301-325. |
| [4] |
HUBER W, HARLEMAN D, RYAN P. Temperature prediction in stratified reservoirs[J]. Journal of the Hydraulics Division, 1972, 98(4): 645-666. |
| [5] |
祝东亮, 李兰, 杨梦斐. 分层型水库垂向水温分布模型解析解研究[J]. 人民长江, 2010, 41(5): 67-70. ( ZHU Dongliang, LI Lan, YANG Mengfei. Research on analytical solution of vertical temperature distribution model for thermal stratification reservoir[J]. Yangtze River, 2010, 41(15): 67-70. DOI:10.3969/j.issn.1001-4179.2010.15.017 (in Chinese)) |
| [6] |
王颖, 臧林, 张仙娥. 河道水温模型及糯扎渡水库下游河道水温预测[J]. 西安理工大学学报, 2003, 19(3): 235-239. ( WANG Ying, ZANG Lin, ZHANG Xian'e. Water temperature of river model and its forecast for downstream flow of Nuozhadu reservoir[J]. Journal of Xi'an University of Technology, 2003, 19(3): 235-239. (in Chinese)) |
| [7] |
刘肖, 陈青生, 魏小旺. 参数率定方案对水温数值模拟结果的影响[J]. 水利水运工程学报, 2014(4): 82-86. ( LIU Xiao, CHEN Qingsheng, WEI Xiaowang. Effects of parameter calibration schemes on numerical simulation results of water temperature[J]. Hydro-Science and Engineering, 2014(4): 82-86. (in Chinese)) |
| [8] |
KARPIK S R, RAITHBY G D. Laterally averaged hydrodynamics model for reservoir predictions[J]. Journal of Hydraulic Engineering, 1990, 116(6): 783-798. DOI:10.1061/(ASCE)0733-9429(1990)116:6(783) |
| [9] |
KUO J T, WU J H, CHU W S. Water quality simulation of Te-Chi reservoir using two-dimensional models[J]. Water Science Technology, 1994, 30(2): 63-72. |
| [10] |
陈小红. 湖泊水库垂向二维水温分布预测[J]. 武汉水利电力学院学报, 1992, 25(4): 376-383. ( CHEN Xiaohong. Prediction of vertical two-dimensional temperature distribution in lakes and reservoirs[J]. Journal of Wuhan University of Hydraulic and Electric Engineering, 1992, 25(4): 376-383. (in Chinese)) |
| [11] |
邓云, 李嘉, 罗麟, 等. 水库温差异重流模型的研究[J]. 水利学报, 2003, 34(7): 7-11. ( DENG Yun, LI Jia, LUO Lin, et al. Temperature prediction model for reservoirs[J]. Journal of Hydraulic Engineering, 2003, 34(7): 7-11. (in Chinese)) |
| [12] |
丁正锋, 钱新, 张玉超, 等. ELCOM模型在流溪河水库水温模拟中的应用[J]. 环境保护科学, 2009, 35(4): 30-33. ( DING Zhengfeng, QIAN Xin, ZHANG Yuchao, et al. Application of ELCOM model in simulating water temperature of Liuxihe reservoir[J]. Environmental Protection Science, 2009, 35(4): 30-33. (in Chinese)) |
| [13] |
李兰, 武见. 梯级水库三维环境流体动力学数值预测和水温分层与累积影响规律研究[J]. 水动力学研究与进展(A辑), 2010, 25(2): 155-164. ( LI Lan, WU Jian. The three-dimensional environmental fluid dynamics code model for research of reservoir water temperature law[J]. Chinese Journal of Hydrodynamics(SerA), 2010, 25(2): 155-164. (in Chinese)) |
| [14] |
马方凯, 江春波, 李凯. 三峡水库近坝区三维流场及温度场的数值模拟[J]. 水利水电科技进展, 2007, 27(3): 17-20. ( MA Fangkai, JIANG Chunbo, LI Kai. Numerical simulation of 3D flow field and temperature field near dam area of Three Gorges reservoir[J]. Advances in Science and Technology of Water Resources, 2007, 27(3): 17-20. (in Chinese)) |
| [15] |
任华堂, 陈永灿, 刘昭伟. 三峡水库水温预测研究[J]. 水动力学研究与进展(A辑), 2008, 23(2): 141-148. ( REN Huatang, CHEN Yongcan, LIU Zhaowei. Study on water temperature prediction in Three Gorges reservoir[J]. Chinese Journal of Hydrodynamics(SerA), 2008, 23(2): 141-148. (in Chinese)) |
| [16] |
华祖林, 储克坚. 温差剪切分层流运动特性试验与数值模拟研究[M]. 北京: 科学出版社, 2008. ( HUA Zulin, CHU Kejian. Experiment and numerical simulation of hydrodynamic characteristics of temperature stratified flow[M]. Beijing: Science Press, 2008. (in Chinese))
|
| [17] |
王鳌然. 水电站进水口分层取水水文试验研究[D]. 天津: 天津大学, 2008. (WANG Aoran. Experimental study on the water temperature at a multi-level intake structure of hydropower station[D]. Tianjin: Tianjin University, 2008. (in Chinese))
|
| [18] |
何洁. 水库分层取水及其水温变化试验和数值模拟研究[D]. 北京: 中央民族大学, 2013. (HE Jie. Physical test and numerical simulation research about water temperature change in different layers of the reservoir[D]. Beijing: Minzu University of China, 2013. (in Chinese))
|
 2017
2017