基于网络层次分析法的节水型社会综合评价

引用本文 [复制中英文]

李岱远, 高而坤, 吴永祥, 等. 基于网络层次分析法的节水型社会综合评价[J]. 水利水运工程学报, 2017(2): 29-37. DOI: 10.16198/j.cnki.1009-640X.2017.02.004.

LI Daiyuan, GAO Erkun, WU Yongxiang, et al. Comprehensive evaluation of water-saving society based on analytic network process[J]. Hydro-science and Engineering, 2017(2): 29-37. (in Chinese) DOI: 10.16198/j.cnki.1009-640X.2017.02.004.

[复制英文]

基金项目

国家自然科学基金资助项目(51479222)；水利部公益性行业科研专项(201301002)

作者简介

李岱远(1994—)，男，山西吕梁人，硕士研究生，主要从事水资源管理方面的研究。E-mail: dyli@nhri.cn。

文章历史

收稿日期：2016-05-27

Contents Abstract Full text Figures/Tables PDF

基于网络层次分析法的节水型社会综合评价

李岱远 ¹, 高而坤 ^1,2, 吴永祥 ¹, 王高旭 ¹, 万永静 ³

1. 南京水利科学研究院水文水资源与水利工程科学国家重点实验室，江苏南京 210029;
2. 水利部水资源司，北京 100053;
3. 河海大学，江苏南京 210098

收稿日期：2016-05-27

基金项目：国家自然科学基金资助项目(51479222)；水利部公益性行业科研专项(201301002)

作者简介：李岱远(1994—)，男，山西吕梁人，硕士研究生，主要从事水资源管理方面的研究。E-mail: dyli@nhri.cn.

摘要: 节水型社会综合评价对全面深入推进节水工作具有重要作用。针对评价指标之间相互影响的客观事实，将网络层次分析法引入节水型社会综合评价中。以常熟市为例，首先构建节水型社会评价指标体系，并分析各指标之间的相互作用关系，运用Super Decisions软件建立ANP模型，通过求解超矩阵确定指标权重。其次对2008—2012年间节水型社会建设程度进行综合评价计算，并与AHP法的评价结果比较。结果表明，常熟市节水型社会建设推进迅速，2008年时综合评价分值低于合格值，节水型社会水平较低；2012年分值接近90，达到较优水平，基本建立了与现代化相适应的节水防污型社会。该评价结果与AHP法的评价结果基本一致，且更加符合常熟市的实际情况，验证了网络层次分析法的科学合理性以及在综合评价节水型社会建设中具有良好的应用前景。

关键词: 节水型社会综合评价网络层次分析层次分析法

建设节水型社会作为中国“两型”社会建设的重要组成和先导实践，是协调中国经济社会持续发展与水资源稀缺有限性矛盾、缓解水资源开发利用外部性、实现水资源可持续利用的战略措施^[1]。2002年“节水型社会”被正式写入《水法》，规定“发展节水型工业、农业和服务业，建立节水型社会”。随着试点经验推广，节水型社会建设正在全面推进。作为节水型社会建设的一个重要组成部分，综合评价、定量分析某一地区水资源状况，准确把握该地区节水型社会建设程度以及发展趋势，有助于政府及相关部门制定切实可行的方案，有效推进节水型社会建设。

随着应用数学发展，国内学者不断将新方法引入节水型社会评价研究中，以期获得更加客观准确的结果。张兴芳^[2]运用系统动力学理论，对城市节水(用水)系统发展水平进行评价，同时认为综合评价研究有利于城市的可持续发展；王巧霞等^[3]基于集对分析理论，对年楚河流域节水型社会建设进行了研究; 2012年，我国颁布了《节水型社会的评价指标体系和评价方法》(GB/T 28284—2012)，标准中推荐采用层次分析法(AHP)，其核心是将系统划分层次，且只考虑上层元素对下层元素的支配作用^[4-6]；车娅丽等^[7]以“压力-状态-响应”PSR模型为基础，与主成分分析法耦合来研究节水型社会的建设水平。这些成果为节水型社会综合评价研究提供了借鉴，但也存在不足。在节水型社会评价指标体系中，各指标并非彼此独立，而是相互影响，系统的结构更类似于网络结构。为克服这种缺陷，国外学者提出网络层次分析法用于综合评价研究，例如Toosi等^[8]运用ANP法综合评估调水工程。基于国内外学者的研究，本文将引入网络层次分析法(ANP)应用于节水型社会建设试点城市——常熟市的综合评价研究中。

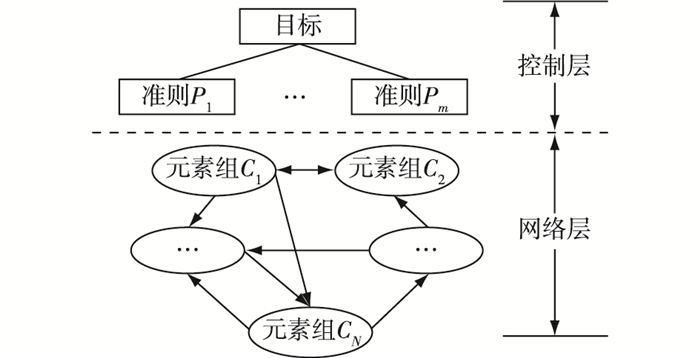
1 基于网络层次分析法的综合评价 1.1 网络层次分析法 1.1.1 构造ANP结构

1996年，在AHP法的基础上T. L. Saaty较为系统地提出了ANP的理论与方法，相对于AHP递阶层次结构，ANP更为复杂。网络层次分析法将系统元素分为两大部分，第一部分称为控制元素层，包括问题目标及决策准则；第二部分为网络层，由所有受控制层支配的元素组成，元素之间相互依存，相互支配，相互影响，递阶结构中的每个准则支配的不是一个简单的内部独立元素，而是一个相互依存、反馈的网络结构^[9-11]。典型ANP层次结构如图 1所示。

图 1 典型的ANP结构 Figure 1 Typical structure of ANP model

在实际问题中，首先进行系统分析，组合形成元素集。其次构造控制层次，先界定决策目标，再界定决策准则，各个准则相对决策目标的权重用AHP法得到。最后构造网络层次，归类确定每一个元素集，分析其网络结构和相互影响关系。

1.1.2 构造超矩阵W

设ANP控制层中有m个元素P₁, P₂, …, P_m，网络层中有N个元素组C₁, C₂, …, C_N，其中C_i包含有n_i个元素e_i1, e_i2，…, e_{in_i}(i=1，2，…，N)。以控制层元素P_s(s=1，2，…，m)为准则，以元素组C_j中元素中的e_jl(l=1，2，…，n_j)为次准则，元素组C_i中的n_i个元素按其对元素的e_jl(l=1，2，…，n_j)的影响力大小进行间接优势度比较，即通过1~9标度法构造如下判断矩阵：

表

由特征根法以及归一化处理，求得排序向量：(ω_i1^jl，ω_i2^jl, …, ω_in^jl)^T，并且得到超矩阵的子块W_ij如式(1)：

$ {\mathit{\boldsymbol{W}}_{ij}} = \left[\begin{array}{l} \omega _{i1}^{j1}\;\;\omega _{i1}^{j2}\;\; \cdots \;\;\;\omega _{i1}^{j{n_j}}\\ \omega _{i2}^{j1}\;\;\omega _{i2}^{j2}\;\; \cdots \;\;\;\omega _{i2}^{j{n_j}}\\ \;\; \vdots \;\;\;\;\;\;\; \vdots \;\;\;\;\; \vdots \;\;\;\;\;\; \vdots \;\\ \omega _{i{n_i}}^{j1}\;\;\omega _{i{n_i}}^{j2}\;\; \cdots \;\;\;\omega _{i{n_i}}^{j{n_j}} \end{array} \right] $

(1)

这里W_ij的列向量就是C_i中元素e_i1, e_i2，…, e_{in_i}对C_j中元素e_j1, e_j2，…, e_{jn_j}的影响程度排序向量。若C_j中元素不受C_i中元素的影响，则W_ij=0。最终获得超矩阵W:

$ \mathit{\boldsymbol{W}} = \left[\begin{array}{l} {W_{11}}\;\;{W_{12}}\;\; \cdots \;\;{W_{1N}}\\ {W_{21}}\;\;{W_{22}}\;\; \cdots \;\;{W_{2N}}\\ \; \vdots \;\;\;\;\;\; \vdots \;\;\;\;\;\; \vdots \;\;\;\;\; \vdots \\ {W_{N1}}\;{W_{N2}}\; \cdots \;\;{W_{NN}}\; \end{array} \right] $

(2)

1.1.3 加权超矩阵$\boldsymbol{\varpi} $

以控制层元素P_s(s=1，2，…，m)为准则，以元素组C_j(j=1，2，…，N)为次准则，根据1~9标度法，构造判断矩阵，求得各元素组对元素组C_j(j=1，2，…，N)的重要性权重并进行归一化，得到排序向量(a_1j, a_2j, …, a_Nj)^T，其中与C_j无关的元素组对应的分向量为零。求得每一个元素组对应的排序向量，由此得到加权矩阵A如式(3)，并按照式(4) 求得加权超矩阵$ \boldsymbol{\varpi} $。

$ \mathit{\boldsymbol{A = }}\left[\begin{array}{l} {a_{11}}\;\;{a_{12}}\;\; \cdots \;\;{a_{1N}}\\ {a_{21}}\;\;{a_{22}}\;\; \cdots \;\;{a_{2N}}\\ \; \vdots \;\;\;\;\;\; \vdots \;\;\;\;\; \vdots \;\;\;\;\; \vdots \\ {a_{N1}}\;{a_{N2}}\; \cdots \;\;{a_{NN}} \end{array} \right] $

(3)

$ \boldsymbol{\varpi} = {a_{ij}}{\mathit{\boldsymbol{W}}_{ij}} $

(4)

1.1.4 极限超矩阵W^∞

加权超矩阵$\boldsymbol{\varpi} $的元素${\varpi _{ij}} $反映了元素i对元素j的一步优势度。i对j的优势度还可以用$\sum\limits_{k = 1}^N {{\varpi _{ik}}{\varpi _{kj}}} $表示，即$ \varpi _{ij}^2$，称为二步优势，它就是W²的元素，W²仍然是列归一化的。若${\mathit{\boldsymbol{W}}^\infty } = \mathop {\lim }\limits_{t \to \infty } \varpi _{ij}^t $存在时，W^∞的第j列表示以控制层元素P_s为准则，网络层中各元素对应元素j的极限相对排序向量。

1.2 综合评价结果计算 1.2.1 权重的确定

ANP计算权重的核心工作，即解超矩阵，是非常复杂的计算过程。因此文中利用Thomas Saaty博士开发的Super Decisions软件进行超矩阵计算，该软件主要应用于层次分析法(AHP)和网络层次分析法(ANP)。利用Super Decisions软件可以构建网络层次结构，并通过输入判断矩阵，自动生成超矩阵、加权超矩阵以及极限超矩阵。其中极限超矩阵的列向量中，各指标对应分向量的值为权重。

1.2.2 指标的规范化处理

各评价指标常具有不同的量纲，不能直接对比，因此需对指标值进行规范化处理。对越大越优的指标采用式(5)，对越小越优的指标采用式(6)。得到无量纲的规范化值，其大小处于0~100区间。

$ {Z_{\rm{s}}} = 100-\frac{{{Z_{\rm{u}}}-Z}}{{{Z_{\rm{u}}}}} \times 100 $

(5)

$ {Z_{\rm{s}}} = \left[{1-\frac{{Z-{Z_{\rm{u}}}}}{{{Z_{\rm{m}}}-{Z_{\rm{u}}}}} \times 100} \right] $

(6)

式中：Z_s为指标规范化值；Z为指标值；Z_u为指标最优值(可以试点的远期目标值作为最优值)；Z_m为指标最大值。

1.2.3 评价结果计算

根据极限超矩阵得到各指标的权重，利用式(7) 计算综合评价结果。

$ H = \sum\limits_{i = 1}^n {{Z_{is}}{q_i}} $

(7)

式中：H为综合评价值；Z_is为第i个指标规范化值；q_i为第i个指标的权重。

2 实例应用 2.1 研究区概况

常熟市地处江苏省东南部(东经121°33′~121°03′，北纬31°31′~31°05′)，太湖下游，长江之滨，襟江带湖，山川相间。该地区属北亚热带季风气候，年平均气温15.4 ℃，年平均降水量1 030.8 mm，年平均蒸发量1 100 mm。地势由西北向东南倾斜，全市面积1 264 km²。该市具有悠久的人文历史、秀丽的山湖景色以及丰饶的物产资源，被誉为“鱼米之乡”。2008年以来，常熟市政府在建设国家节水型城市的同时，开始了国家节水型社会的建设。

2.2 评价指标体系

科学构建节水型社会评价指标体系是客观反映节水型社会发展水平的关键环节。根据《节水型社会评价指标体系和评价方法》(GB/T 28284—2012)、常熟市水资源管理报告以及节水型社会建设自评估报告等信息，结合实际用水情况，构建了评价指标体系见表 1^[12-16]。

表 1 常熟市节水型社会评价指标体系 Table 1 Index system of water-saving society for Changshu city

以2015年常熟市各指标的规划目标值作为最优值，通过常熟市以及周边地区的统计资料分析确定各指标的最大值。依据式(5) 和(6) 的规范化处理方法，对常熟市2008—2012年各指标的统计值进行无量纲化，结果见表 2。

表 2 指标值规范化结果 Table 2 Results of standardized indexes

考核指标	最大值	最优值	规范化值(无量纲)
考核指标	最大值	最优值	2008	2009	2010	2011	2012
水分生产率(kg/m³)	-	1.3	89.23	1.33	90.73	1.36	91.47
灌溉水利用系数	-	0.7	85.71	87.14	87.14	90.00	91.43
城镇生活人均综合用水量(L/(人·d))	300	150	79.60	69.07	63.13	59.60	57.80
节水器具普及率(%)	-	100	80.00	89.00	94.00	96.00	97.00
供水管网漏损率(%)	18	12	48.75	60.00	65.00	68.75	71.25
万元工业增加值用水量(m³)	40	16	53.33	69.17	76.25	82.92	92.08
工业用水重复利用率(%)	-	85	80.71	84.35	87.41	90.35	93.18
水功能区水质达标率(%)	-	70	39.57	51.14	62.29	83.14	92.29
城市生活污水集中处理率%	-	98	88.78	89.29	95.41	97.96	98.98
万元GDP用水量(m³)	195.1	80	26.59	32.67	54.65	82.97	93.40
计划用水率(%)	-	100	90.00	94.00	96.00	97.00	98.00
人均GDP(万元)	-	226 485	47.68	50.96	60.16	70.76	77.95

表 2 指标值规范化结果 Table 2 Results of standardized indexes

2.3 建立网络层次分析模型 2.3.1 ANP结构

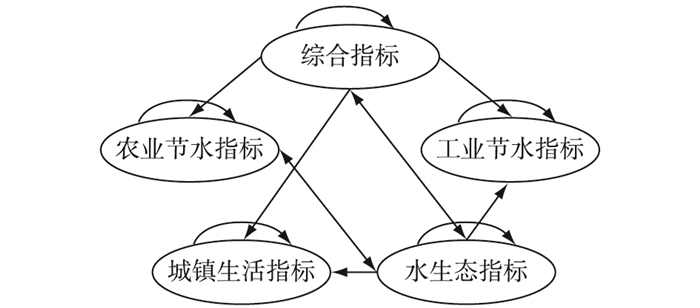
在节水型社会综合评价中，ANP模型的控制层为一层结构，换言之，目标和准则均为节水型社会发展水平。网络层中，根据各评价指标簇之间相互作用关系在Super Decisions软件中建立如图 2所示的网络结构(从一个指标簇指向另一个指标簇的箭头表明第2个指标簇中的元素对第1个指标簇中的元素具有影响作用)。

图 2 ANP模型网络层结构 Figure 2 Structure of network layer in ANP model

2.3.2 各指标权重计算结果

(1) 在综合评价中各指标簇的权重计算。以水生态指标簇的影响因素权重计算为例，依据1.1.3中加权矩阵的计算方法，在Super Decisions软件中构建判断矩阵并通过特征根法求出排序向量，即权重值，结果见表 3。

表 3 水生态指标簇的影响因素判断矩阵以及权重 Table 3 Judgment matrix and weight of factors influencing ecological index clusters

同上，分别以农业节水指标、城镇生活指标、工业节水指标和综合指标为准则，计算指标簇的权重值见表 4。

表 4 各指标簇权重 Table 4 Weights of each index cluster

(2) 构建节水型社会综合评价模型的初始超矩阵。构建初始超矩阵需要所有具有相关关系的元素之间两两比较。比如，水功能区水质达标率E1与城镇生活指标簇中的元素有相关关系。以水功能区水质达标率E1为准则，构建判断矩阵，并求出权重，如表 5所示。

表 5 城镇生活指标簇中影响指标E1的元素判断矩阵以及权重 Table 5 Judgment matrix and weight of factors in urban living index cluster influencing E1

分别对网络层中的每一个元素进行上述分析，得到初始超矩阵，见表 6。

表 6 初始超矩阵 Table 6 Unweighted super matrix

考核指标		A		L			I		E		Z
考核指标		A1	A2	L1	L2	L3	I1	I2	E1	E2	Z1	Z2	Z3
A	A1	0	0	0	0	0	0	0	0.250	0	0.5	0.667	0
A	A2	1	0	0	0	0	0	0	0.750	0	0.5	0.333	0
L	L1	0	0	0	0	0	0	0	0.540	0.750	0	1	0
	L2	0	0	0.333	0	0	0	0	0.163	0	0	0	0
	L3	0	0	0.667	0	0	0	0	0.297	0.250	0	0	0
I	I1	0	0	0	0	0	0	0	0.750	0	0.8	0.667	0
I	I2	0	0	0	0	0	0	0	0.250	0	0.2	0.333	0
E	E1	1	0	0	0	0	0	0	0	0	0	1	0
E	E2	0	0	0	0	0	1	0	1	0	0	0	0
Z	Z1	0	0	0	0	0	0	0	0.594	0	0	0.8	0
	Z2	0	0	0	0	0	0	0	0.249	0	0	0	0
	Z3	0	0	0	0	0	0	0	0.157	0	1	0.2	0

表 6 初始超矩阵 Table 6 Unweighted super matrix

(3) 节水型社会综合评价模型的加权超矩阵。依据式(4)，比如水生态指标-城镇生活指标子矩阵块，将子矩阵中的6个数字分别与表 4中第2行第4列的元素0.087相乘。通过这种运算得到加权超矩阵，如表 7所示。

表 7 加权超矩阵 Table 7 Weighted super matrix

考核指标		A		L			I		E		Z
考核指标		A1	A2	L1	L2	L3	I1	I2	E1	E2	Z1	Z2	Z3
A	A1	0	0	0	0	0	0	0	0.017	0	0.076	0.086	0
A	A2	0.750	0	0	0	0	0	0	0.052	0	0.076	0.043	0
L	L1	0	0	0	0	0	0	0	0.047	0.75	0	0.087	0
	L2	0	0	0.333	0	0	0	0	0.014	0	0	0	0
	L3	0	0	0.667	0	0	0	0	0.026	0.25	0	0	0
I	I1	0	0	0	0	0	0	0	0.212	0	0.236	0.165	0
I	I2	0	0	0	0	0	1	0	0.071	0	0.059	0.083	0
E	E1	0.250	0	0	0	0	0	0	0	0	0	0.070	0
E	E2	0	0	0	0	0	0	0	0.112	0	0	0	0
Z	Z1	0	0	0	0	0	0	0	0.266	0	0	0.373	0
	Z2	0	0	0	0	0	0	0	0.112	0	0	0	0
	Z3	0	0	0	0	0	0	0	0.071	0	0.553	0.093	0

表 7 加权超矩阵 Table 7 Weighted super matrix

(4) 节水型社会综合评价模型的极限超矩阵。运用Super Decisions软件对加权超矩阵进行幂运算，令幂指数趋近无穷，直至每列元素不再变化，这样得到了极限超矩阵，如表 8所示。

表 8 极限超矩阵 Table 8 Extreme super matrix

考核指标		A		L			I		E		Z
考核指标		A1	A2	L1	L2	L3	I1	I2	E1	E2	Z1	Z2	Z3
A	A1	0.021	0	0	0	0	0	0	0.021	0	0.021	0.021	0
A	A2	0.088	0	0	0	0	0	0	0.088	0	0.088	0.088	0
L	L1	0.084	0	0	0	0	0	0	0.084	0	0.084	0.084	0
	L2	0.066	0	0	0	0	0	0	0.066	0	0.066	0.066	0
	L3	0.046	0	0	0	0	0	0	0.046	0	0.046	0.046	0
I	I1	0.242	0	0	0	0	0	0	0.242	0	0.242	0.242	0
I	I2	0.076	0	0	0	0	0	0	0.076	0	0.076	0.076	0
E	E1	0.025	0	0	0	0	0	0	0.025	0	0.025	0.025	0
E	E2	0.013	0	0	0	0	0	0	0.013	0	0.013	0.013	0
Z	Z1	0.280	0	0	0	0	0	0	0.280	0	0.280	0.280	0
	Z2	0.012	0	0	0	0	0	0	0.012	0	0.012	0.012	0
	Z3	0.047	0	0	0	0	0	0	0.047	0	0.047	0.047	0

表 8 极限超矩阵 Table 8 Extreme super matrix

2.4 节水型社会的综合评价

由上述极限超矩阵，可知各指标的权重见表 9。

表 9 各指标的权重 Table 9 Weights of each index

根据式(7) 计算2008—2012年常熟市节水型社会建设综合评价结果，并与《节水型社会的评价指标体系和评价方法》标准推荐方法AHP的计算结果进行对比，见表 10。

表 10 2008—2012常熟市节水型社会综合评价结果 Table 10 Comprehensive evaluation of water-saving society in Changshu, from 2008 to 2012

2.5 综合评价结果分析

由表 10可知，ANP法与标准推荐方法AHP评价结果基本相同，仅2008和2009年的评价结果稍有差异。常熟市从2008年开始，在全市范围内开展节水型社会创建工作，即2008—2009年期间，节水型社会建设程度较低，处于起步阶段，因此ANP的评价结果更加符合实际情况。随着政府工作的加强，水资源管理制度和水利发展规划体系的完善，公众节水意识的提高，坚持节水减排的建设方向，特别是实施科技创新战略，推进传统产业集约用水，优化产业布局，狠抓节水载体建设，有效控制用水总量，大大提高了水资源的利用效率，促进了常熟市节水型社会的发展。到2012年常熟市基本建立了与现代化相适应的节水防污型社会，其中万元GDP用水量由2008年的164.5 m³降至2012年的87.6 m³。总体来说，考虑评价指标间相互作用关系的ANP法更加科学合理地反映了节水型社会建设的程度以及发展情况。

3 结语

(1) 利用网络层次分析法进行节水型社会综合评价时，分析其网络结构和各指标间相互影响关系，构建ANP的超矩阵，通过计算机软件Super Decisions求解超矩阵得出相应的权重，最后结合指标的规范化值计算综合评价结果并判断所属的评价等级，概念清晰，结构简单。

(2) 通过建立网络层结构，遵循了各指标之间相互影响的客观事实，克服了层次分析法中假设元素之间彼此独立的缺点，使得结果更加科学合理，在决策和规划中具有参考价值。

(3) 此评价方法存在一定缺陷，利用1~9标度法构造判断矩阵时，主观因素影响较大，容易使评价结果失真。因此构造超矩阵的方法有待进一步研究，使得评价结果更加客观真实。

参考文献

[1]	王建华, 陈明. 中国节水型社会建设理论技术体系及其实践应用[M]. 北京: 科学出版社, 2013. ( WANG Jianhua, CHEN Ming. Theory and practice of China water saving society construction[M]. Beijing: Science Press, 2013. (in Chinese))
[2]	张兴芳. 运用动力学和可持续发展观点探讨城市节水水平评判方法[J]. 系统辩证学学报, 2000, 8(2): 72-76. ( ZHANG Xingfang. A study of assessment methods of urban water conservation in views of system dynamics and sustainable development[J]. Journal of Systemic Dislectics, 2000, 8(2): 72-76. (in Chinese))
[3]	王巧霞, 袁鹏, 谢勇. 集对分析在节水型社会建设评价中的应用研究[J]. 水电能源科学, 2011, 29(9): 134-137. ( WANG Qiaoxia, YUAN Peng, XIE Yong. Application of set pair analysis to evaluation of water-saving society construction[J]. Water Resources and Power, 2011, 29(9): 134-137. (in Chinese))
[4]	GB/T 28284—2012节水型社会评价指标体系和评价方法[S]. (GB/T 28284—2012 Index system and methods for assessment of water-saving society[S]. (in Chinese))
[5]	张炳江. 层次分析法及其应用案例[M]. 北京: 电子工业出版社, 2014: 14-15. ( ZHANG Bingjiang. The theory and application examples of analytic hierarchy process[M]. Beijing: Publishing House of Electronics Industry, 2014: 14-15. (in Chinese))
[6]	徐海洋, 杜明侠, 张大鹏, 等. 基于层次分析法的节水型社会评价研究[J]. 节水灌溉, 2009(7): 31-34. ( XU Haiyang, DU Mingxia, ZHANG Dapeng, et al. Research on evaluation of water saving society construction based on AHP method[J]. Water-saving Irrigation, 2009(7): 31-34. (in Chinese))
[7]	车娅丽, 徐慧, 龚李莉, 等. 基于PSR模型和主成分分析法的节水型社会建设评价[J]. 水电能源科学, 2014, 32(7): 124-127. ( CHE Yali, XU Hui, GONG Lili, et al. Evaluation method of water-saving society establishment based on PSR framework and principal component analysis[J]. Water Resources and Power, 2014, 32(7): 124-127. (in Chinese))
[8]	TOOSI S L R, SAMANI J M V. Evaluating water transfer projects using analytic network process (ANP)[J]. Water Resources Management, 2012, 26(7): 1999-2014. DOI:10.1007/s11269-012-9995-2
[9]	萨迪T L. 网络层次分析法原理及其应用——基于利益、机会、成本及风险的决策方法[M]. 鞠彦兵, 刘建昌, 译. 北京: 北京理工大学出版社, 2015. (SAATY T L. Theory and applications of the analytic network process: decision making with benefits, opportunities, costs, and risks[M]. Translated by JU Yanbing, LIU Jianchang. Beijing: Beijing Institute of Technology Press, 2015. (in Chinese))
[10]	杜栋, 庞庆华, 吴炎. 现代综合评价方法与案例精选[M]. 北京: 清华大学出版社, 2005. ( DU Dong, PANG Qinghua, WU Yan. The methods and cases of modern comprehensive evaluation[M]. Beijing: Tsinghua University Press, 2005. (in Chinese))
[11]	高娟. 基于网络层次分析对风险投资项目选择方法的研究[D]. 杭州: 浙江大学, 2008. (GAO Juan. Research on venture investment program's selecting basing on ANP method[D]. Hangzhou: Zhejiang University, 2008. (in Chinese))
[12]	常熟市人民政府. 常熟市节水型社会建设自评估报告[R]. 常熟: 常熟市人民政府, 2013. (Changshu Municipal Government. The assessment report of Changshu's water-saving society[R]. Changshu: Changshu Municipal Government, 2013. (in Chinese))
[13]	陈莹, 赵勇, 刘昌明. 节水型社会评价研究[J]. 资源科学, 2004(6): 83-88. ( CHEN Ying, ZHAO Yong, LIU Changming. Evaluation indication system of water conservation society[J]. Resources Science, 2004(6): 83-88. (in Chinese))
[14]	陈莹, 刘昌明, 赵勇. 节水及节水型社会的分析和对比评价研究[J]. 水科学进展, 2005, 16(1): 82-87. ( CHEN Ying, LIU Changming, ZHAO Yong. Adoption of water conservation practices in the society and comparison evaluation study[J]. Advances in Water Science, 2005, 16(1): 82-87. (in Chinese))
[15]	张熠, 王先甲. 节水型社会建设评价指标体系构建研究[J]. 中国农村水利水电, 2015(8): 118-120, 125. ( ZHANG Yi, WANG Xianjia. Research on the index system of water-saving society construction in China[J]. China Rural Water Conservancy and Hydropower, 2015(8): 118-120, 125. (in Chinese))
[16]	苏州市水利(水务)局. 苏州市水利"十二五"规划[R]. 苏州: 苏州市人民政府, 2011. (Suzhou Water Authority. The 12th five-year water plan of Suzhou[R]. Suzhou: Suzhou Municipal Government, 2011. (in Chinese))

Comprehensive evaluation of water-saving society based on analytic network process

LI Daiyuan¹, GAO Erkun^1,2, WU Yongxiang¹, WANG Gaoxu¹, WAN Yongjing³

1. State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Nanjing Hydraulic Research Institute, Nanjing 210029, China;
2. Department of Water Resources of the Ministry of Water Resources, Beijing 100053, China;
3. Hohai University, Nanjing 210098, China

Abstract: A comprehensive evaluation of the water-saving society is significant for promoting thorough water saving. Aiming at the objective fact that evaluation indexes are interactional, an analytic network process is used for assessment of the water-saving society. Taking the Changshu city as an example, the evaluation index system of the water saving society is built and the interaction between the indexes is revealed. On the basis of the above analysis, the ANP model, which calculates weights of each index by solving super matrix, is established by the software—Super Decisions. The results of ANP comprehensive evaluation from 2008 to 2012 which can reflect the level of the water-saving society are calculated and compared with the AHP model. Analysis results show that the development of the water-saving society is rapid in the Changshu city. In 2008, the score of comprehensive evaluation was lower than the qualified grade, indicating that water saving was at a low level in the Changshu city. But in 2012, the score was close to 90. In other words, the Changshu city keeps its development at a high speed and establishes a water-saving and pollution-prevention society adapted to modernization. The results of ANP model are in accordance with the AHP model. And the results are more suitable with the actual situation in the Changshu city, which demonstrates that ANP model is scientific and reasonable, and has a favorable application prospect in comprehensive evaluation of the water-saving society.

Key words: water-saving society comprehensive evaluation analytic network process analytic hierarchy process