2. 南京水利科学研究院,江苏 南京 210029
潮流能是海洋可再生能源的一种,是指潮流做水平运行所含有的动能。与其他海洋能资源如潮汐能、波浪能、温差能、盐差能以及海洋风能等相比,潮流能具有以下几个特点:①较强的规律性和可预测性;②功率密度大,能量稳定;③对海洋环境影响较小,不需要修建大坝,不会产生大的噪声,不影响人们的视觉环境,可以保持良好的地域生态环境。因此,潮流能在全球范围内具有广阔的应用前景。我国20世纪80年代对全国沿海的潮流能总量进行了初步估算[1],各海区潮流能分布以东海最强,主要分布在长江口和舟山海域;渤海和黄海次之,其中渤海主要为辽东半岛老铁山水道,黄海主要分布在江苏斗龙港至小洋口一带;南海沿岸最弱,主要分布在台湾海峡、琼州海峡附近[2]。
潮流能的计算方法主要有两种:基于能通量方法和基于动力分析方法[3]。前者以Farm方法和Flux方法[4-5]为代表,后者以Grattre和Cummins提出的方法[6-7]为代表。其中Farm方法基于发电机能量转换原理,与设备及其布置有关;Flux基于能量直接转换,与设备无关;两种方法思路清晰,计算方便,应用较广。Grattre和Cummins方法中的潮流能流基于水体通量[3],主要针对小海湾和两端为开敞水域的水道。由于早期潮流能估算主要基于现场实测流速数据,而现场实测数据十分稀缺,潮流能估算往往采用个别测点代表整个断面或整条水道,误差较大。针对该问题,通过数值模拟途径获得数据结果进行潮流能估算是一种很好的弥补方法,被广泛应用于不同海域的潮流能估算[8-9]。本文借助数值模拟方法,首先建立江苏沿海潮流数学模型,通过实测资料对模型进行验证;在分析江苏沿海潮流特性的基础上,对重点区域潮流能进行估算,为江苏沿海潮流能开发提供技术参考。
1 江苏海岸形势与潮汐分布江苏省海岸线北起苏鲁交界的绣针河口,南抵长江口北支,海岸线长约954 km。江苏省海岸大致可分为3段:北部海州湾和废黄河三角洲岸段、中部射阳河口至弶港岸段和南部的辐射沙洲岸段。从海岸地貌上,江苏海岸大致可分为4个地貌单元:废黄河三角洲平原区、中部海积平原区、长江三角洲平原区和辐射沙脊群分布区。
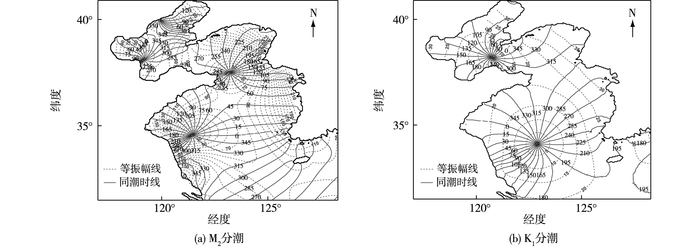
江苏沿海受两大潮波系统控制,分别为自南向北传播的东海前进潮波和受山东半岛和朝鲜半岛阻挡形成的自北向南推进逆时针旋转潮波系统,两股潮波系统在弶港岸外辐合。图 1(a)为M2潮汐分布,无潮点位于废黄河口外,逆时针方向旋转的M2分潮潮波系统控制着整个辐射沙洲以北的江苏海域潮波运动。海州湾为该旋转潮波系统的波腹区,M2分潮振幅在150~170 cm。波节点位于废黄河口外海,振幅小于100 cm。该旋转潮波在新洋港附近明显受到东海前进潮波的作用,南侧的辐射沙洲海域为两股潮波系统共同作用海域。在湾顶弶港附近M2分潮振幅达180 cm以上。图 1(b)为K1分潮同潮图,受黄海中央逆时针方向旋转潮波系统影响(无潮点122°53′17.7″E,34°06′38.2″),K1分潮振幅相对较小,一般约15~20 cm,对江苏海岸潮汐影响也相对较小。
|
图 1 江苏沿海M2和K1分潮潮汐分布 Figure 1 Distribution of M2 and K1 tidal constituent along Jiangsu coasts |
采用静压假定、刚盖假定和Boussineq近似,并认为水流垂线不均匀分布产生的积分修正系数为1.0,描述水流基本运动方程Navier-Stokes可简化为沿水深平均的平面二维浅水方程,在球面坐标系下:
| $\frac{{\partial h}}{{\partial t}} + \frac{1}{{R{\rm{cos}}\varphi }}\left( {\frac{{\partial h\bar u}}{{\partial \lambda }} + \frac{{\partial h\bar v{\rm{cos}}\varphi }}{{\partial \varphi }}} \right) = 0$ | (1) |
| $\begin{array}{l} \frac{{\partial h\bar u}}{{\partial t}} + \frac{1}{{R{\rm{cos}}\varphi }}\left( {\frac{{\partial h{{\bar u}^2}}}{{\partial \lambda }} + \frac{{\partial h\overline {vu} {\rm{cos}}\varphi }}{{\partial \varphi }}} \right) = \left( {f + \frac{{\bar u}}{R}{\rm{tan}}\varphi } \right)\\ \bar vh - \frac{1}{{R{\rm{cos}}\varphi }}gh\frac{{\partial \eta }}{{\partial x}} - \frac{{{\tau _{{\rm{b}}x}}}}{{{\rho _0}}} + \frac{\partial }{{\partial x}}\left( {h{T_{xx}}} \right) + \frac{\partial }{{\partial y}}\left( {h{T_{xy}}} \right) \end{array}$ | (2) |
| $\begin{array}{l} \frac{{\partial h\bar v}}{{\partial t}} + \frac{1}{{R{\rm{cos}}\varphi }}\left( {\frac{{\partial h\overline {uv} }}{{\partial \lambda }} + \frac{{\partial h{{\bar v}^2}{\rm{cos}}\varphi }}{{\partial \varphi }}} \right) = - \left( {f + \frac{{\bar u}}{R}{\rm{tan}}\varphi } \right)\\ \bar uh - \frac{1}{R}gh\frac{{\partial \eta }}{{\partial y}} - \frac{{{\tau _{{\rm{b}}y}}}}{{{\rho _0}}} + \frac{\partial }{{\partial x}}\left( {h{T_{yx}}} \right) + \frac{\partial }{{\partial y}}\left( {h{T_{yy}}} \right) \end{array}$ | (3) |
式中:h=η+d为总水深,η为潮位,即以参考基面为准的水面位置,d为海底到参考基面距离;λ,φ分别为经度和纬度,u,v分别为λ,φ方向垂线平均流速;u=R cosφdλ/dt,v=Rdφ/dt;t为时间;f为科氏系数(f=2ωsinφ,ω为地球自转角速度,φ为所在地区的纬度);g为重力加速度,g=9.8 m/s2;τbx,τby为底部摩擦项,
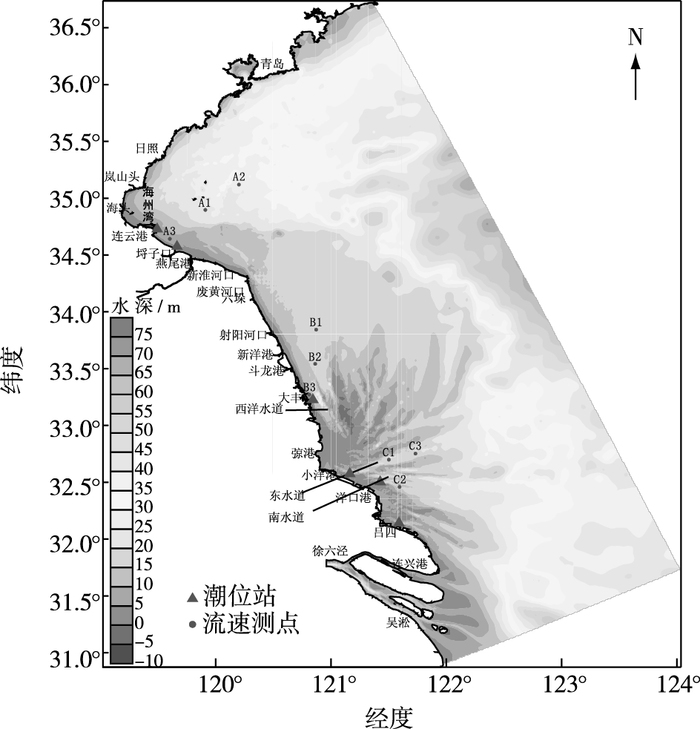
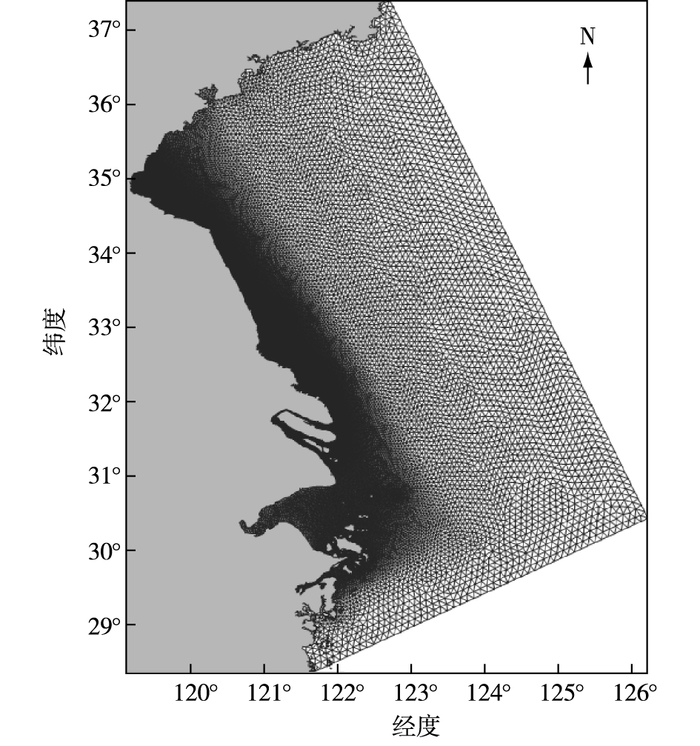
模拟区北边界位于山东半岛成山头附近,南边界位于浙江瓯江口附近,外海边界与江苏岸线基本平行,距离岸边300 km左右。模型采用经纬度球坐标系统,最小网格控制在100 m左右。模型网格单元数95 125个,节点数49 023个。图 2为江苏沿海地形分布,图 3为江苏沿海潮流模型计算范围和计算网格。
|
图 2 江苏沿海地形 Figure 2 Bathymetric chart of Jiangsu coasts |
|
图 3 潮流数学模型计算范围和计算网格 Figure 3 Domain and grids of tidal current model for Jiangsu coasts |
模型开边界条件由西北太平洋潮波模型[10]计算提供。闭边界满足不可入条件。初始边界采用冷启动。模型采用目前流行的Mike21软件计算,基于非结构有限体积法[11]计算。水平紊动扩散系数采用Smagorinsky公式计算,其中cs取0.28;曼宁系数M根据调试取60。
2.3 模型验证由于缺少统一大范围的水文测验资料,采用不同时期验证资料对模型进行验证,包括6个潮位站和9个流速测点。6个潮位站分别为连云港、埒子口、大丰、吕四、小洋港和洋口站;9个流速测点分别位于连云港海域、射阳河口、洋口港海域,见图 2。实测资料时间:连云港海域资料时间在2012年7月4—13日期间,射阳河口海域资料在2013年6月2—11日期间,辐射沙洲洋口港海域时间在2005年5月24—31日期间。3次测量资料的潮位和流速流向验证表明,潮流模型计算的潮位和流速、流向过程与实测结果吻合较好,表明模型边界条件、参数选取等是合适的。
2.4 潮流特性图 4为江苏沿海典型涨落潮流场。从图 4可以看出,辐射沙洲外海涨潮流主要分东南、西北、东北三支向辐射沙洲中部弶港湾顶运动;其东南支由长江口外海涨潮流形成,西北支为连云港至废黄河口外海落潮流沿中部海岸线进入辐射沙洲海区,而东北支为外海涨潮流。进入辐射沙洲区以后,西北、东南、西南向涨潮流沿着各自沙脊水道向湾顶运动。由于潮时的差别,辐射沙洲海域处于涨潮时,连云港、海州湾海域正处于落潮状态,落潮流总体沿着E向退出海湾,两侧近岸主要沿着岸线走向运动;同时也可以看出,二者存在相互关联,连云港南翼落潮流正是辐射沙洲东北支涨潮流的一部分,体现潮波的来回“震荡”运动。落潮时,湾顶水域落潮流呈150°的扇面角向外海辐散,退出沙洲海域。废黄河口至海州湾的涨潮流主要由沿鲁东岸线南下的涨潮流和少部分辐射沙洲海域退出的落潮水流组成。后者相对较弱,主要影响灌河口以东水域。
|
图 4 江苏沿海典型流态 Figure 4 Typical flow fields of Jiangsu coasts |
江苏沿海以规则半日潮流为主。从潮流性质上区分,辐射沙洲外海为典型的旋转流,潮流主轴不明显;辐射沙洲近岸水域,潮流主要为沿沙脊通道的往复流。往北,尤其是新洋港至废黄河口之间海域,潮流以往复流为主。由废黄河口至海州湾,潮流旋转流性质又有所加强,尤其在连云港外海。连云港南北两翼椭圆率稍小,潮流主轴方向明显。图 5为江苏沿海潮流矢量图。同样为旋转流,连云港海域与辐射沙洲海域旋转方向相反。北部海州湾、连云港海域潮流为逆时针方向旋转(左旋),南部辐射沙洲海域潮流为顺时针方向旋转(右旋)。二者分界线在废黄河口一带。
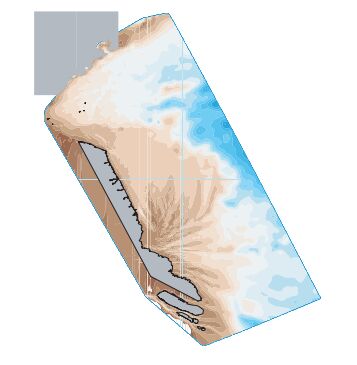
|
图 5 潮流矢量椭圆图 Figure 5 Sketch of tidal current vector ellipses |
江苏沿海以规则半日潮流为主,潮流最大可能流速按下式计算:
| $\begin{array}{l} {\overrightarrow V _{{\rm{max}}}} = 1.295{\overrightarrow W _{{{\rm{M}}_{\rm{2}}}}} + 1.245{\overrightarrow W _{{{\rm{S}}_{\rm{2}}}}} + {\overrightarrow W _{{{\rm{K}}_{\rm{1}}}}} + \\ \quad \quad {\overrightarrow W _{{{\rm{O}}_{\rm{1}}}}} + {\overrightarrow W _{{{\rm{M}}_{\rm{4}}}}} + {\overrightarrow W _{{\rm{S}}{{\rm{M}}_{\rm{2}}}}} \end{array}$ | (4) |
式中:
根据2013年6月1—15日半个月的潮流数值模拟结果,进行潮流准调和分析[12],可以得到6个分潮的准调和常数,继而得到江苏沿海潮流的可能最大流速,见图 6。从图 6可以看出,从燕尾港以南至吕四港附近,江苏沿海潮流最大可能流速均大于2.0 m/s,具备潮流能开发的流速要求。其中,废黄河口附近和辐射沙洲顶部区域,潮流速较大;废黄河口附近局部最大可能流速超过3.2 m/s,辐射沙洲顶部区域最大可能流速超过3.5 m/s。海州湾海域潮流较弱,最大可能流速约0.7~1.0 m/s。
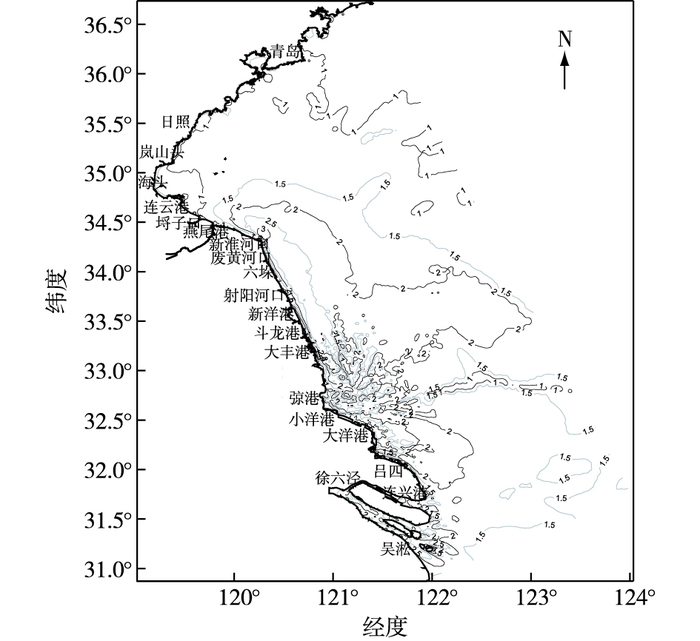
|
图 6 潮流可能最大流速分布(单位:m/s) Figure 6 Distribution of probable maximum tidal current (unit: m/s) |
由于Grattre和Cummins提出的方法主要针对小海湾和小水道(指两端连通开敞水域的水道),在江苏沿海不适用,这里采用Farm方法和Flux方法能通量方法进行分析。
潮流能可以理解为单位体积水体含有的潮流动能(即能量密度),还可以理解为单位时间通过单位面积的潮流动能(即能流密度)[3]。结合实际应用,采用能流密度P来表示:
| $P = \rho {V^3}/2$ | (5) |
式中:ρ为海水密度;V为潮流流速。由于潮流速随时间变化,通常采用某时段内的平均值。根据我国郑志南[13]提出的计算方法,半月潮周期内平均能流密度Pa为:
| ${P_{\rm{a}}} = \frac{1}{{12{\rm{ \mathsf{ π} }}}}\left( {5 + 3\left( {\frac{{{V_{\rm{n}}}}}{{{V_{\rm{s}}}}}} \right) + 3{{\left( {\frac{{{V_{\rm{n}}}}}{{{V_{\rm{s}}}}}} \right)}^2} + 5{{\left( {\frac{{{V_{\rm{n}}}}}{{{V_{\rm{s}}}}}} \right)}^3}} \right){P_{\rm{m}}}$ | (6) |
式中:Vs,Vn分别为大潮、小潮期间最大流速;Pm为最大能流密度,Pm=0.5ρVs3=0.5ρ(1+K)Vsn3,其中,K=(Vs-Vn)/(Vs+Vn)为流速波动系数;Vsn=(Vs+Vn)/2为平均流速。
求得平均能流密度后,根据Farm方法,可开发的总潮流能PE为:
| ${P_{\rm{E}}} = {P_{\rm{a}}}{A_{\rm{s}}}{\eta _{\rm{t}}}n$ | (7) |
式中:As=πD2/4,为单台发电涡轮机涡轮转子扫过的面积;D为转子直径。ηt为发电总效率,ηt=Cpηgearηgeneratorηtrans,Cp,ηgear,ηgenerator,ηtrans分别为涡轮机效率、齿轮传动效率、发电机效率和电力传输效率,n为发电机个数。
根据Flux方法,总潮流能为:
| ${P_{\rm{E}}} = {P_{\rm{a}}}{A_{{\rm{cs}}}}{P_{{\rm{SIF}}}}$ | (8) |
式中:Acs为垂直于潮流方向的断面面积;PSIF是指在不产生显著环境或经济影响的前提下,可供开发利用的潮流能占总潮流能资源的百分比,一般为10%~20%[13]。
基于江苏沿海潮流数学模型2013年6月1—15日模拟结果,借助以上方法,首先得到平均潮流能流密度分布(图 7)。可见,江苏沿海燕尾港以南水域平均潮流能流密度均在200 W/m2以上。其中能流密度最高的废黄河口附近(E1)平均能流密度最大值在1 050 W/m2左右;辐射沙洲水道,平均能流密度基本在700 W/m2以上,弶港北部的西洋水道(E2)、小洋港东水道(E3)平均能流密度最大值均可达1 200 W/m2,小洋港南水道附近(E4)局部在900 W/m2以上,可见江苏沿海理论上的潮能流相当大。

|
图 7 平均潮流能流密度分布(单位:W/m2) Figure 7 Distribution of averaged tidal current energy density (unit: W/m2) |
采用Farm方法估算单机功率。根据目前发电装置,转子直径D取10 m,总效率取35%[3]。则废黄河口附近单机功率可达28.8 kW。弶港北部的西洋水道、小洋港东水道局部单机功率可达33.0 kW,小洋港南水道附近局部在24.7 kW。
由于Farm方法中的总潮流能计算涉及发电机组的布置,故采用Flux方法估算总潮流能。废黄河口附近潮流能最大的4 km宽范围内,断面平均水深约8 m,断面面积约0.32 km2,PSIF取15%[3],计算得到总潮流能为5.0 MW。辐射沙洲海域因断面分布较复杂,西洋水道平均能流密度超过1 200 W/m2的水域宽约3 km,平均水深约10 m,断面面积约0.30 km2,同样PSIF取15%,计算得到总潮流能为5.4 MW。小洋港东水道总潮流能为3.0 MW(宽1.5 km,断面平均水深12.0 m,平均能流密度1 100 W/m2),南水道总潮流能为5.3 MW(宽2.5 km,断面平均水深17.0 m,平均能流密度830 W/m2)。
当然,以上潮流能估算结果为根据模型计算得到的理论值,实际潮流能开发还需要考虑环境影响,总潮流能也根据发电装置不同而有不同变化。
5 结语(1) 江苏沿海辐射沙洲外海为典型的旋转流,潮流主轴不明显;辐射沙洲近岸水域,潮流主要为沿沙脊通道的往复流;北侧新洋港至废黄河口之间,潮流以往复流为主;废黄河口至海州湾,潮流旋转流性质有所加强,连云港外海旋转流性质相对明显。北部海州湾、连云港海域潮流为逆时针方向旋转(左旋),南部辐射沙洲海域潮流为顺时针方向旋转(右旋)。二者分界线在废黄河口一带。
(2) 江苏沿海燕尾港以南至吕四港附近,潮流最大可能流速均大于2.0 m/s。其中,废黄河口附近和辐射沙洲顶部区域,潮流速较大;废黄河口附近局部最大可能流速超过3.2 m/s,辐射沙洲顶部区域最大可能流速超过3.5 m/s。海州湾海域潮流较弱,最大可能流速约0.7~1.0 m/s。
(3) 江苏沿海燕尾港以南水域平均潮流能流密度均在200 W/m2以上。其中废黄河口附近、辐射沙洲水道能流密度相对集中。废黄河口附近平均能流密度最大值在1 050 W/m2左右;辐射沙洲水道局部最大值均可达1 200 W/m2。废黄河口附近潮流能最大的4.0 km宽范围内,总潮流能为5.0 MW。辐射沙洲海域水道局部可达5.4 MW。
| [1] |
王传昆, 陆德超. 中国沿海农村海洋能资源区划[R]. 国家海洋局科技司, 水电部科技司, 1989. (WANG Chuankun, LU Dechao. Marine energy resources division of China's coastal areas[R]. Department of Science and Technology of State Oceanic Administration, Department of Science and Technology of the Ministry of Water Resources and Power, 1989. (in Chinese))
|
| [2] |
李允武. 海洋能源开发[M]. 北京: 海洋出版社, 2008: 99-101. ( LI Yunwu. Development and utilization of marine renewable energy[M]. Beijing: Ocean Press, 2008: 99-101. (in Chinese))
|
| [3] |
吕新刚, 乔方利. 海洋潮流能资源估算方法研究进展[J]. 海洋科学进展, 2008, 26(1): 98-108. ( LV Xingang, QIAO Fangli. Advances in study on tidal current energy resource assessment methods[J]. Advances in Marine Sience, 2008, 26(1): 98-108. (in Chinese)) |
| [4] |
Black & Veatch Consulting Ltd. UK, Europe, and global tidal energy resource assessment. Marine energy challenge (Report No.107799/D/2100/05/)[R]. London: Carbon Trust, 2004.
|
| [5] |
Black & Veatch Consulting Ltd. Phase Ⅱ, UK tidal stream energy resource assessment. Marine energy challenge (Report No.107799/D/2200/03)[R]. London: Carbon Trust, 2005.
|
| [6] |
GARRETT C, CUMMINS P. Generating power from tidal currents[J]. Waterway Port Coastal Ocean Eng, 2004, 130: 114-118. DOI:10.1061/(ASCE)0733-950X(2004)130:3(114) |
| [7] |
GARRETT C, CUMMINS P. The power potential of tidal currents in channels[J]. Proc Roy Soc(A), 2005, 461: 2563-2572. DOI:10.1098/rspa.2005.1494 |
| [8] |
吕新刚, 乔方利, 赵昌, 等. 海洋潮流能资源的数值估算——以胶州湾口为例[J]. 太阳能学报, 2010, 31(2): 137-143. ( LV Xingang, QIAO Fangli, ZHAO Chang, et al. Numerical evaluation of tidal stream energy resources in the ocean: a case study in Jiaozhou Bay mouth[J]. Acta Energiae Solaris Sinica, 2010, 31(2): 137-143. (in Chinese)) |
| [9] |
王智峰, 周良明, 张弓贲, 等. 舟山海域特定水道潮流能估算[J]. 中国海洋大学学报(自然科学版), 2010, 40(8): 27-33. ( WANG Zhifeng, ZHOU Liangming, ZHANG Gongben, et al. Tidal stream energy assessment in specific channels of Zhoushan sea area[J]. Periodical of Ocean University of China (Natural Science), 2010, 40(8): 27-33. (in Chinese)) |
| [10] |
章卫胜, 张金善, 林瑞栋, 等. 中国近海潮汐变化对外海海平面上升的响应[J]. 水科学进展, 2013, 24(2): 243-250. ( ZHANG Weisheng, ZHANG Jinshan, LIN Ruidong, et al. Tidal response of sea level rise in marginal seas near China[J]. Advances in Water Science, 2013, 24(2): 243-250. (in Chinese)) |
| [11] |
DHI. MIKE 21 & MIKE 3 Flow Model FM hydrodynamic and transport module scientific documentation[Z]. 2012.
|
| [12] |
方国洪, 郑文振, 陈宗镛, 等. 潮汐和潮流的分析和预报[M]. 北京: 海洋出版社, 1986. ( FANG Guohong, ZHENG Wenzhen, CHEN Zongyong, et al. Analysis and prediction of tidal level and tidal current[M]. Beijing: Ocean Press, 1986. (in Chinese))
|
| [13] |
郑志南. 海洋潮流能的估算公式[J]. 哈尔滨船舶工程学院学报, 1987, 8(2): 37-44. ( ZHENG Zhinan. Estimating formulae of ocean tidal current energy[J]. Journal of Harbin Shipbuilding Engineering Institute, 1987, 8(2): 37-44. (in Chinese)) |
2. Nanjing Hydraulic Research Institute, Nanjing 210029, China
 2017
2017 