2. 河海大学 港口海岸与近海工程学院,江苏 南京 210098;
3. 南京水利科学研究院,江苏 南京 210029
潜堤是一种常用的护岸工程建筑物,一般是指淹没在水中的防护堤。潜堤广泛应用于护岸、保滩促淤、围海造田、防浪、挡沙和导流等海岸工程中。潜堤的消浪特性是人们广为研究的课题,而透浪系数是衡量潜堤削弱波浪能量的主要指标。波浪越过潜堤时,一部分波能被反射,另一部分波能由于堤顶水深限制导致波浪破碎而损耗。所以,潜堤堤后波高主要与入射波要素、潜堤的几何尺寸和水深等因素有关。
潜堤透浪系数的研究主要有物理模型试验和数值模拟两种方法,物理模型试验是目前国内外采用较多的研究方法。杨正己等[1]通过在波浪水槽中的物理模型试验得出规则波作用下的潜堤透浪系数经验公式。Van der Meer[2]利用前人及本身试验测量结果,认为潜堤透浪系数仅为堤顶淹没水深与入射波有效波高比值的函数。邹红霞等[3]通过物理模型试验研究了不规则波作用下抛石潜堤的透射系数以及堤后稳定波高的统计分布。冯卫兵等[4]通过物理模型试验研究分析了影响潜堤透射系数的各个因素,并且分别拟合出规则波和不规则波情况下的潜堤透浪系数。而在数模方面,张娜等[5]运用断面物理模型试验和数值模拟相结合的方法,进行港内带有潜堤及透浪式建筑物的总平面布置可行性研究。江鸣[6]基于Flow3D软件中的k-ε模型以及VOF自由表面追踪法,建立了垂向二维数值波浪水槽模型,对系列矩形潜堤附近的波浪运动进行了研究。贾晓等[7]应用BW模型基于孔隙层的设置来模拟反射边界和透射建筑物。
波浪数值计算模型主要基于缓坡方程[8-9]、能量平衡方程[10-11]及Boussinesq型方程[12]。其中Boussinesq方程是在时域内求解质量和动量守恒方程,可以模拟出波浪传播过程中波面的变化、水下质点运动和波浪破碎等信息。目前应用比较成熟的商业软件主要有MIKE21-BW模型及Delft3D Bousssinesq模块,开源软件有Funwave等。其中MIKE21-BW模型是基于Boussinesq型方程的时域数值解,同时考虑了波浪的非线性和弥散性,可以精确模拟小范围的波浪传播变形。
本文采用MIKE21-BW模型进行规则波作用下的潜堤透浪系数的数值模拟。
1 控制方程MIKE21-BW模型控制方程如下:
连续方程:
| $n\frac{{\partial \xi }}{{\partial t}} + \frac{{\partial P}}{{\partial x}} + \frac{{\partial Q}}{{\partial y}} = 0$ | (1) |
X向动量方程:
| $\begin{array}{l} n\frac{{\partial P}}{{\partial t}} + \frac{\partial }{{\partial x}}\left( {\frac{{{P^2}}}{h}} \right) + \frac{\partial }{{\partial y}}\left( {\frac{{PQ}}{h}} \right) + \frac{{\partial {R_{xx}}}}{{\partial x}} + \frac{{\partial {R_{xy}}}}{{\partial y}} + {F_x} + {n^2}gh\frac{{\partial \xi }}{{\partial x}} + \\ {n^2}P\left( {\alpha + \beta \frac{{\sqrt {{P^2} + {Q^2}} }}{h}} \right) + \frac{{gP\sqrt {{P^2} + {Q^2}} }}{{{h^2}{C^2}}} + n{\mathit{\Psi }_1} = 0 \end{array}$ | (2) |
Y向动量方程:
| $\begin{array}{l} n\frac{{\partial Q}}{{\partial t}} + \frac{\partial }{{\partial y}}\left( {\frac{{{Q^2}}}{h}} \right) + \frac{\partial }{{\partial x}}\left( {\frac{{PQ}}{h}} \right) + \frac{{\partial {R_{yy}}}}{{\partial y}} + \frac{{\partial {R_{xy}}}}{{\partial x}} + {F_y} + {n^2}gh\frac{{\partial \xi }}{{\partial y}} + \\ {n^2}Q\left( {\alpha + \beta \frac{{\sqrt {{P^2} + {Q^2}} }}{h}} \right) + \frac{{gQ\sqrt {{P^2} + {Q^2}} }}{{{h^2}{C^2}}} + n{\mathit{\Psi }_2} = 0 \end{array}$ | (3) |
式中: n为孔隙率;ξ为水位(m);t为时间(s);x,y为笛卡尔坐标(m);h为水深(m),h=d+ξ;d为静止水位时水深(m);P,Q分别为x,y方向的流量密度(m3·m-1·s-1);Rxx,Ryy和Rxy为水滚引起的非均匀流动所产生的附加质量;g为重力加速度(m/s2);ψ1和ψ2为Boussinesq方程的色散项;Fx,Fy为x,y方向的水平应力;α为多孔介质中的层流阻力系数;β为多孔介质中的湍流阻力系数;C为谢才阻力系数。
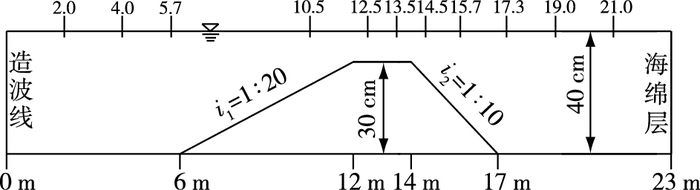
2 模型验证 2.1 Dingemans潜堤地形Dingemans对淹没潜堤地形上的波浪传播进行了物理模型试验,其试验结果被一些学者用来验证数值模拟[13]。笔者采用的模型验证资料取自文献[13],模型的地形、水深及测点布置如图 1所示。
|
图 1 Dingemans试验布置及测点位置 Figure 1 Location of measuring points in Dingemans test |
设置1个波浪数值水槽,长21.0 m,左端为造波边界,右端为消波边界,水槽静水深度为0.4 m,在距离入流边界5.7 m处设置1个梯形潜堤,前坡坡度i1=1:20,后坡坡度i2=1:10,堤顶宽度为2.0 m,堤顶水深为0.1 m。图中上方数值表示测波仪离造波线的距离(单位:m),用来采集测点的波面历时变化。
2.2 模型设置采用BW模型进行数值模拟时,入射波高H=20 cm,波周期T=2.02 s。计算网格取ΔX=ΔY=0.1 m,时间步长Δt=0.01 s,模拟总步长为10 001步,入射波采用单向规则波。在模型计算中选取了图 1中所标明的11个断面进行模拟(距离造波线2.0~21.0 m间共有11个测点)。
2.3 参数率定模型参数的取值是否合理,对于模拟计算结果的精确性至关重要。在BW模型中,主要率定的参数是曼宁数M。它是反映水流流动时所受阻力的一个综合系数,与谢才系数的关系如下:
| $M = C/{h^{1/6}}$ | (4) |
式中:C为谢才系数;h为水深。
通过不断调整曼宁数M的大小,使得潜堤前后的波面过程与物理模型试验的波面过程趋于一致。在数值水槽的潜堤段,曼宁数M取为15;而在非潜堤段,M取为32。
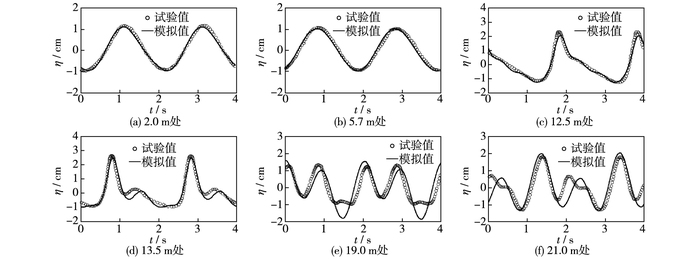
2.4 验证结果由于篇幅所限,文中只列出具有代表性的6个测点的计算结果,这6个测点位置分别为距离造波线2.0,5.7,12.5,13.5,19.0和21.0 m。图 2为这6个测点波面过程模拟值与试验值比较,其中纵轴表示波面值,横轴表示时间历程。
|
图 2 各测点处波面过程试验值与模拟值的比较 Figure 2 Comparison between simulated and experimental values of wave surface at each measuring point |
通过对比可以看出,波浪爬上潜堤后,计算的堤前、堤顶和堤后波面曲线与实测曲线基本一致。在遇到潜堤前,即2.0和5.7 m处测点,曲线吻合很好,说明造波方法正确;在堤顶处,即12.5和13.5 m处测点,由于水深开始变浅,波浪开始非线性变化,波峰更为尖陡,波谷更加平缓,模拟值与实测值吻合较好;在堤后处,即19.0和21.0 m处测点,次峰开始增长,而主峰的波高相对于之前略有下降,传至堤后常水深处,出现了多个波峰,也就是说主峰和次峰己经不再明显,由于波浪的较强频散性,模拟值与试验值的偏差稍大于堤前和堤顶的测点,但总体上吻合较好。
3 模型计算与成果分析 3.1 模型设置BW模型采用的波浪数值水槽与李鹏[14]的物理模型试验水槽相类似(见图 3)。具体布置如下:潜堤布置在离造波线35 m处,堤身高度为30 cm,通过改变水深h来实现相对淹没水深(a/H)的改变(a为静水位到堤顶高度);i1,i2分别为潜堤前后坡坡度,认为i2对消浪影响不大,记i1=i2= i;水槽两端均布置有海绵层,以消除边界波浪反射所造成的影响。

|
图 3 波浪数值水槽 Figure 3 Diagram of numerical wave flume |
模型计算范围取为80 m×20 m的矩形区域,网格大小为ΔX=ΔY=0.1 m,时间步长为Δt=0.01 s,入射波采用单向规则波,波高H为10 cm,其他波浪要素见表 1。
| 表 1 规则波作用下模型计算波浪要素 Table 1 Wave elements under action of regular waves |
潜堤堤后波高采用与物理模型试验类似的方法采集数据,在堤后2倍入射波波长处开始记录波高,每隔1个波长记录1个数据,堤后共记录4个测点,然后将这4个测点波高的平均值作为潜堤堤后稳定波高。
3.2 规则波作用下各因子对潜堤消浪效果的影响 3.2.1 影响因素分析潜堤透浪系数可以定义为:堤后稳定比波高,即堤后波高(HT)与入射波高(HI)的比值。而潜堤透浪主要由两部分组成,一部分是由于波浪爬越堤顶产生的越浪,另一部分是因为堤身具有孔隙,波浪通过孔隙渗透会对堤后波高产生影响,本文不考虑堤身渗透对堤后波高所产生的影响。
研究入射波特性和潜堤几何尺寸的变化对透浪系数的影响,主要包括:入射波的波高H,波长L,静水位到堤顶的高度a,堤顶宽度B,潜堤坡度i。
根据已有试验结果[1, 14]可知,影响潜堤透浪系数的主要因素可以通过以下无因次参数来表达:
| ${K_{\rm{t}}} = \frac{{{H_{\rm{T}}}}}{{{H_{\rm{I}}}}} = f\left( {\frac{a}{H},\frac{H}{L},\frac{B}{H},i} \right)$ | (5) |
式中:
相对淹没深度(a/H)直接影响到波浪反射、越顶及在堤顶破碎的形态,是影响堤后波高的重要因素(潜堤时a/H<0,未出水时a/H=0)。从模型计算结果(图 4)可以看出,当规则波在潜堤上传播,随着相对淹没深度(a/H)的增大,堤后消浪效果越好。当a/H=-0.5~0时,波浪在爬坡过程中发生破碎,越浪成为堤后波浪的主要组成部分。当a/H=-1.5~-1.0时,波浪破碎不完全,消浪效果明显降低。

|
图 4 a/H对透浪系数的影响 Figure 4 Influences of a/H on wave transmission coefficient |
在文献[1]的物理模型试验中,当
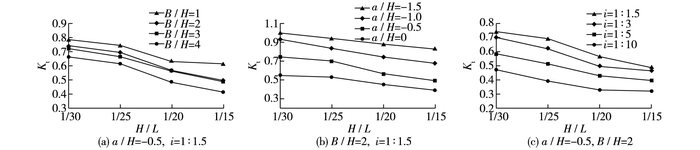
波陡(H/L)是影响波浪破碎形态的重要因素,模型计算结果见图 5。在图 5(a)中,同一相对淹没深度和潜堤坡度情况下,对于不同波陡,堤后相对波高变化趋势基本一致,图 5(b)和5(c)中也有类似变化规律。坦波作用时,会有大量水体越过堤顶,而且越堤时发生破碎所对应的水深较小,所以其他影响因素不变时,坦波的消浪效果不如陡波。
|
图 5 H/L对透浪系数的影响 Figure 5 Influences of H/L on wave transmission coefficient |
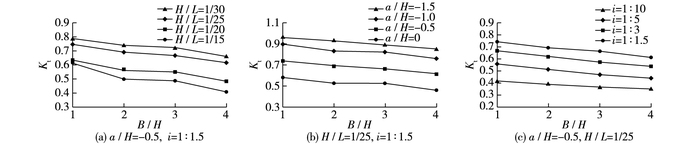
相对堤顶宽度(B/H)影响波浪越堤时的破碎水深,也是影响堤后波高的重要因素,模型计算结果见图 6。从图 6可见,其他影响因素不变的情况下,相对堤顶宽度变大,堤后相对波高变小,说明消浪效果越好;同时,相对堤顶宽度在一定的a/H条件下才起作用,当a/H≤ -1时,增加相对堤顶宽度消浪效果变化不大。总之,堤后相对波高随着相对堤顶宽度的增大而减小,但当水深变大时,相对堤顶宽度对消浪的影响明显减小。
|
图 6 B/H对透浪系数的影响 Figure 6 Influences of B/H on wave transmission coefficient |
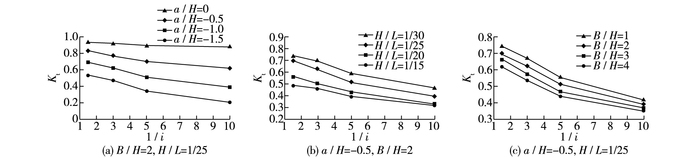
潜堤坡度也是对堤后波高产生影响的因素之一,模型计算结果见图 7。潜堤坡度取值分别为i=1:1.5,1:3,1:5,1:10。从图 7可见,在其他影响因素不变情况下,潜堤坡度越大,堤后相对波高越小。但只有在一定的a/H条件下,坡度变化引起的堤后波高才会呈现出规律,当a/H≤-1.5时,增加潜堤坡度对消浪效果基本没有作用。
|
图 7 i对透浪系数的影响 Figure 7 Influences of change in i on wave transmission coefficient |
潜堤透浪系数的影响因素有相对淹没水深(a/H)、相对堤顶宽度(B/H)、波陡(H/L)、潜堤坡度(i),建立规则波作用下潜堤透浪系数计算式的形式为:
| ${K_{\rm{t}}} = 1 - {\rm{tanh}}\left( {{k_1}\frac{a}{H} + {k_2}\frac{H}{L}} \right) - {k_3}{\rm{exp}}\left( { - \frac{B}{H}} \right)\left[ {1 - {\rm{exp}}\left( {{k_4}\xi } \right)} \right]$ | (6) |
式中:k1,k2,k3,k4为待定系数;
应用MATLAB数学软件,对数据进行非线性回归,求出待定系数。拟合出规则波作用下潜堤透浪系数计算公式为:
| ${K_{\rm{t}}} = 1 - {\rm{tanh}}\left( {0.34\frac{a}{H} + 16.12\frac{H}{L}} \right) - 121.76{\rm{exp}}\left( { - \frac{B}{H}} \right)\left[ {1 - {\rm{exp}}\left( {0.001{\rm{ }}5\xi } \right)} \right]$ | (7) |
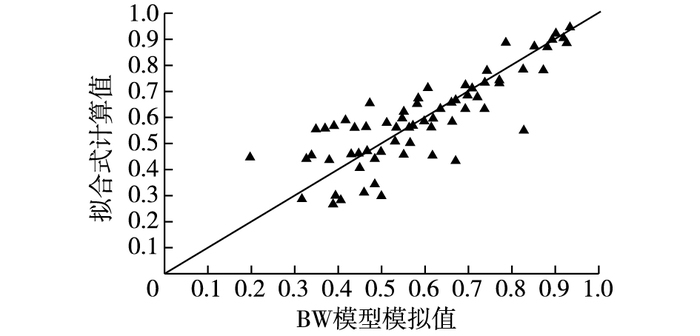
潜堤透浪系数模拟值与拟合式计算值的比较见图 8,由图可知,拟合的相关系数为0.858,残差平方和为0.801,拟合效果较好。
|
图 8 透浪系数模拟值与拟合式计算值比较 Figure 8 Comparison between simulated and fitting formula calculated values of wave transmission coefficient |
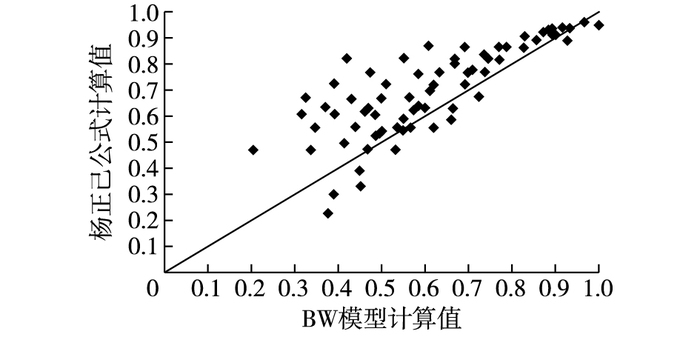
图 9为BW模型计算值与杨正己公式计算值的比较,从图可以看出,绝大多数BW模型计算值小于杨正己公式计算的透浪系数值。原因之一是杨正己的物理模型试验采用的是透水抛石堤,本文数值模拟采用不透水堤,不透水堤的消浪效果较好,从而导致透浪系数偏小;另一个原因是本文研究的潜堤坡度包括i=1:1.5,1:3,1:5,1:10,而杨正己的试验潜堤坡度为i=1:2。从模型计算结果可知,其他影响因素不变时,潜堤坡度越大,消浪效果越好,从而导致BW模型计算的潜堤透浪系数偏小。
|
图 9 透浪系数模拟值与杨正己公式计算值比较 Figure 9 Comparison of simulated and Yang Zhengji's formula calculated values of wave transmission coefficient |
当潜堤坡度i=1:2时,对杨正己公式与本文拟合公式进行了进一步的比较(如图 10)。图 10(a)是潜堤透浪系数随波陡的变化,两种公式随波陡的变化而引起的差值很小;图 10(b)是潜堤透浪系数随相对浸没深度的变化,杨正己公式计算的透浪系数值总体上大于本文计算值,当a/H较大或者较小时,两者基本吻合;图 10(c)是潜堤透浪系数随相对堤顶宽度的变化,当B/H较小时,两者差值较大,当B/H较大时,差值不断变小。总体来看,本文的潜堤透浪系数计算式与杨正己公式具有较好的吻合度。

|
图 10 H/L,a/H,B/H的变化对透浪系数的影响 Figure 10 Influences of changes in H/L, a/H and B/H on wave transmission coefficient |
采用MIKE21-BW模型对规则波作用下潜堤的透浪系数进行了二维数值模拟。采用Dingemans物理模型试验结果对BW模型进行参数率定和验证,验证结果良好。在此基础上,分析了潜堤透浪系数的无因次影响参数,主要包含相对淹没水深(a/H)、相对堤顶宽度(B/H)、波陡(H/L)、潜堤坡度(i),对不同影响因素组合情况分别进行模拟计算。建立了规则波作用下潜堤透浪系数的计算式形式,应用MATLAB数学软件对式中的系数进行拟合,得出的拟合式计算值与BW模型计算值的相关系数为0.858,残差平方和为0.801。另外,将BW模型计算值与杨正己公式计算值进行比较,对数据的差异进行合理性分析。在本文模拟条件范围以内,拟合式可以用于潜堤透浪系数的估算。
| [1] |
杨正己, 贺辉华, 潘少华. 波浪作用下抛石堤的稳定性及消浪特性[J]. 水利水运科学研究, 1981(3): 34-45. ( YANG Zhengji, HE Huihua, PAN Shaohua. Stability and wave dissipation characteristics of rubble-mound breakwater under wave action[J]. Journal of Nanjing Hydraulic Research Institute, 1981(3): 34-45. (in Chinese)) |
| [2] |
VAN DER MEER J W. Data on wave transmission due to overtopping[R]. Marknesse, The Netherlands: Delft Hydraulics, 1990.
|
| [3] |
邹红霞, 陈国平. 不规则波作用下潜堤透射系数的计算方法及统计分布[J]. 水运工程, 2010(3): 11-16. ( ZOU Hongxia, CHEN Guoping. Analyses of irregular wave of transmission coefficient calculation method and distribution though a submerged breakwater[J]. Port & Waterway Engineering, 2010(3): 11-16. (in Chinese)) |
| [4] |
冯卫兵, 王明明, 崔川川. 潜堤透浪系数的试验研究[J]. 水运工程, 2012(9): 1-6. ( FENG Weibing, WANG Mingming, CUI Chuanchuan. Experimental study of wave transmission coefficient over a submerged breakwater[J]. Port & Waterway Engineering, 2012(9): 1-6. (in Chinese)) |
| [5] |
张娜, 张文忠, 曲淑媛. 潜堤及透浪式建筑物的平面二维波浪数值模拟[C]//第十四届中国海洋(岸)工程学术讨论会论文集, 2009: 676-679. (ZHANG Na, ZHANG Wenzhong, QU Shuyuan. Two-dimensional wave numerical simulation of the submerged breakwater and permeable works[C]//The Fourteenth Chinese Marine (Coastal) Engineering Symposium, 2009: 676-679. (in Chinese))
|
| [6] |
江鸣. 波浪通过系列矩形潜堤的数值模拟[D]. 天津: 天津大学, 2011. (JIANG Ming. Numerical simulation of wave propagation over a series of submerged rectangular dikes[D]. Tianjin: Tianjin University, 2011. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10056-1012023724.htm
|
| [7] |
贾晓, 张峰, 邵燕华. 透浪建筑物掩护水域波浪数值模拟研究[J]. 水运工程, 2013(11): 153-158. ( JIA Xiao, ZHANG Feng, SHAO Yanhua. Wave numerical simulation about waters sheltered by permeable hydraulic structures[J]. Port & Waterway Engineering, 2013(11): 153-158. (in Chinese)) |
| [8] |
季小强. 基于扩展型双曲缓坡方程波浪传播模型[J]. 海洋工程, 2010, 28(3): 59-67. ( JI Xiaoqiang. A wave transmission model based on the extended hyperbolic mild slope equation[J]. The Ocean Engineering, 2010, 28(3): 59-67. (in Chinese)) |
| [9] |
王红川, 周正萍. 基于改进缓坡方程的波浪传播数值模拟[J]. 海洋工程, 2013, 31(3): 45-53. ( WANG Hongchuan, ZHOU Zhengping. Numerical simulation of wave propagation by modified mild-slope equation[J]. The Ocean Engineering, 2013, 31(3): 45-53. (in Chinese)) |
| [10] |
李雪, 董胜, 陈更. 港池泊稳的能量平衡方程数值模拟[J]. 中国海洋大学学报, 2014, 44(7): 100-106. ( LI Xue, DONG Sheng, CHEN Geng. Numerical simulation of energy balance equation of the harbor basin berthing stability[J]. Journal of Ocean University of China, 2014, 44(7): 100-106. (in Chinese)) |
| [11] |
冯春明, 董胜, 吉星明. 基于能量平衡方程的多向随机波数学模型的研究与改进[J]. 海洋湖沼通报, 2013(4): 181-188. ( FENG Chunming, DONG Sheng, JI Xingming. Research and improve for multi-directional random wave mathematical model based on energy-balance-equation[J]. Transaction of Oceanology and Limnology, 2013(4): 181-188. (in Chinese)) |
| [12] |
邹华志. 近岸波浪的Boussinesq型方程模拟及其应用[J]. 广东水利水电, 2009(4): 1-5. ( ZOU Huazhi. Numerical simulation of coastal waves using Boussinesq-type equations and its application[J]. Guangdong Water Resources and Hydropower, 2009(4): 1-5. (in Chinese)) |
| [13] |
冯卫兵, 邵东, 王明明, 等. 高阶非线性完全频散性波浪数值模型及应用[J]. 海洋工程, 2015(1): 49-57. ( FENG Weibing, SHAO Dong, WANG Mingming, et al. The numerical application of a higer-order nonlinear and fully dispersive wave model[J]. The Ocean Engineering, 2015(1): 49-57. (in Chinese)) |
| [14] |
李鹏. 波浪在潜堤上传播和破碎[D]. 南京: 南京水利科学研究院, 2005. (LI Peng. Wave propagation and breaking on submerged breakwater[D]. Nanjing: Nanjing Hydraulic Research Institute, 2005. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-82306-2006012882.htm
|
2. College of Harbor, Coastal and Offshore Engineering, Hohai University, Nanjing 210098, China;
3. Nanjing Hydraulic Research Institute, Nanjing 210029, China
 2017
2017 