近年来我国西部河流上规划兴建了多座高水头单级大型船闸,由于西部山区河流多具有狭窄、落差大等特点,其船闸闸门多为“窄而高”的型式,较之人字闸门一字闸门能够显著降低闸门门体的“高宽比”,在适应山区河流闸门工作水头大、通航水位变幅大、航宽窄等运行条件中具有特殊优势。
国内外对船闸闸门水动力特性的研究,本质上是对过流水体及门体相互作用关系的研究。通过探究不同功能、体型的船闸闸门在不同水头、边界条件等影响作用下,启闭中的非恒定流过程或者全部开启、局部开启的恒定流过程,优化船闸闸门结构布置、边界条件及启闭方式,改善过闸水流流态,为船闸闸门及其启闭机安全运行提供意见及建议。
目前,对带门底间隙的一字闸门转动引起的复杂三维非恒定流模拟,未见相关报道。本文考虑闸门旋转启闭过程的绕流特性,采用在强流线弯曲、漩涡和旋转有更好表现的Realizable k-ε双方程紊流模型进行三维数值模拟,重点关注启闭过程动水阻力矩变化规律。由于一字闸门启闭过程门前后水位差对门体所受动水阻力矩量值的增减起关键作用[1],在模拟中处理自由表面边界条件十分重要,故采用VOF法[2]对自由水面进行捕捉。
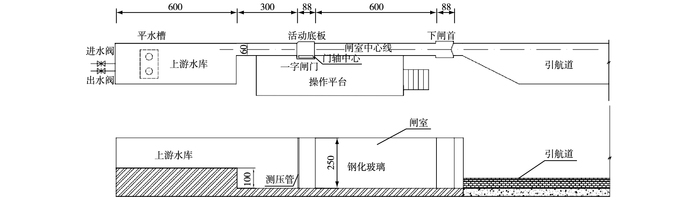
1 一字闸门模型试验按重力相似准则取模型比尺为1:20,满足几何相似、水流运动相似、门体重心相似及启闭机运动相似。针对高水头单级船闸一字闸门设计规模及闸室“窄而高”的特点,将模型布置于0.6 m×2.5 m(宽×高)水槽中。一字闸门门叶尺寸41.0 m×14.8 m×2.1 m(高×长×厚),通过拉压传感器测得直联式启闭机推拉杆受力,据此获得闸门所受动水阻力矩变化过程。采用无线数字波高仪测定闸门前后水位波动值。物理模型整体平面布置见图 1。
|
图 1 物理模型整体平面布置(单位:cm) Figure 1 Layout of a physical model (unit: cm) |
T. Shih等[3]认为,紊动黏性系数计算式中的系数Cμ不应是常数,而与应变率联系起来,从而提出了Realizable k-ε模型,适用于旋转流动。结合研究实际,即高水头船闸一字闸门启闭过程具有较强的三维旋转特性,且门头等区域引起的水体旋转不可忽略,综合考虑精度、计算成本等因素,采用Realizable k-ε紊流模型进行模拟,控制方程如下:
| $\frac{{\partial {\alpha _{\rm{w}}}}}{{\partial t}} + {u_i}\frac{{\partial {\alpha _{\rm{w}}}}}{{\partial {x_i}}} = 0$ | (1) |
动量方程:
| $\frac{{\partial {u_i}}}{{\partial t}} + {u_j}\frac{{\partial {u_i}}}{{\partial {x_j}}} = {f_i} - \frac{1}{\rho }\frac{{\partial p}}{{\partial {x_i}}} + \nu \frac{{{\partial ^2}u}}{{\partial {x_j}\partial {x_j}}}$ | (2) |
k方程:
| $\frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {{\bar u}_j}k} \right)}}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _{\rm{t}}}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k} - \rho \varepsilon $ | (3) |
ε方程:
| $\frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {{\bar u}_j}\varepsilon } \right)}}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _{\rm{t}}}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \rho {C_1}\bar S\varepsilon - {C_2}\rho \frac{{{\varepsilon ^2}}}{{k + \sqrt {\nu \varepsilon } }}$ | (4) |
式中:ρ为流体密度;t为时间;p为压强;ui为速度矢量在xi方向上的分量;ν为运动黏性系数,ν=μ/ρ,μ为动力黏度;fi为xi方向单位体积力;αw为单元中水相的体积分数;μt为紊动黏性系数;μt=Cμρk2/ε,Gk为压力生成项,Cμ=(1/A0+ASU*k/ε);C1=max(0.43,η/(η+5));C2=1.9;σk=1.0,σε=1.2。
Cμ,C1计算式中各参数按以下计算:
| $\begin{array}{l} {A_0} = 4.04;{A_S} = \sqrt 6 {\rm{cos}}\varphi ;\varphi = \frac{1}{3}{\rm{arccos}}\left( {\sqrt 6 W} \right);\\ W = {{\bar S}_{ij}}{{\bar S}_{ik}}{{\bar S}_{kj}}/{({{\bar S}_{ij}}{{\bar S}_{ij}})^{1/2}};{U^*} = {({{\bar S}_{ij}}{{\bar S}_{ij}} + {{\mathit{\tilde \Omega }}_{ij}}{{\mathit{\tilde \Omega }}_{ij}})^{1/2}}; \end{array}$ |
| $\begin{array}{l} {{\mathit{\tilde \Omega }}_{ij}} = {\mathit{\Omega }_{ij}} - 2{\varepsilon _{ijk}}{\omega _k};{\mathit{\Omega }_{ij}} = {{\bar R}_{ij}} - {\varepsilon _{ijk}}{\omega _k};\\ \eta = \frac{k}{\varepsilon }\sqrt {2{{\bar S}_{ij}}{{\bar S}_{ij}}} ;{{\bar S}_{ij}} = \frac{1}{2}\left( {\frac{{\partial {{\bar u}_i}}}{{\partial {x_j}}} + \frac{{\partial {{\bar u}_j}}}{{\partial {x_i}}}} \right);{{\bar R}_{ij}} = \frac{1}{2}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)。\end{array}$ |
引入VOF模型的紊流模型与未引入的紊流模型在形式上一致,但流体特性参数ρ和μ需根据体积分数进行加权平均调整:
| $\rho = {\alpha _{\rm{w}}}{\rho _{\rm{w}}} + (1 - {\alpha _{\rm{w}}}){\rho _{\rm{a}}}$ | (5) |
| $\mu = {\alpha _{\rm{w}}}{\mu _{\rm{w}}} + (1 - {\alpha _{\rm{w}}}){\mu _{\rm{a}}}$ | (6) |
式中:μw和μa分别为水和气的分子黏性系数。
对于气液二相流而言:
| ${\alpha _{\rm{w}}} + {\alpha _{\rm{a}}} = 1$ | (7) |
式中:αa为气相的体积分数,水气交界面通过求解连续方程获得。
采用有限体积法对上述方程进行离散,压力-速度耦合采用PISO算法,对于瞬态问题具有较大优势。
2.2 计算区域及其离散以物理模型试验为依据建模,考虑闸门启闭过程影响,闸室上游边界取距离闸门轴心位置115 m,下游边界取离闸门轴心100 m。计算区域取船闸闸室,宽12 m,门库尺寸长17.6 m,宽3.3 m。考虑门底间隙及门槛的影响,参照模型取门底间隙为2.1 m。采取平面划分混合网格,门库区域为三角形非结构网格,闸室段为结构网格,纵向拉伸为棱柱体网格,初始水位交接面纵向拉伸网格作加密处理。整体网格剖分见图 2。

|
图 2 数学模型计算区域整体网格剖分 Figure 2 Grids for numerical simulation |
为方便计算且不失通用性,取水流的静止状态为初始条件,闸墙及闸室底部边界均为固壁边界。由于上、下游边界距离闸门足够远,考虑静水启闭闸门影响范围及计算成本,将上、下游边界作固壁边界[4-5]。上表面气体边界定义为压力边界。闸门轮廓表面定义为刚体动边界。闸门门底缝隙处作自由出流。
实现一字闸门运行全过程动态仿真研究,核心在于一字闸门启闭过程的动边界处理,动网格更新方法采用2.5D网格重构法[6],指定拉伸面(三角形非结构网格区域)为变形区域,使用局部网格重构结合弹簧光顺法再生网格,实现闸门启闭过程的同时大大减少网格数量,提高网格重构及计算求解过程的效率。动网格计算时间步长取0.05 s,每5个时间步长更新一次网格[7]。
闸门动态开启方式使用FLUENT预定义宏DEFINE_CG_MOTION,定义闸门角速度ω的变化,ω与直联式启闭机布置及启闭机活塞杆运行方式有关[8-9]:
| $\omega \left( t \right) = \frac{{({a_0} + s){\rm{d}}s/{\rm{d}}t}}{{bc{\rm{sin}}({\beta _0} + {\beta _i})}}{\rm{ = }}\frac{1}{L}{\rm{d}}s/{\rm{d}}t$ | (8) |
式中:ω(t)为闸门角速度;s为活塞杆行程;βi为闸门运转角度(关闭过程由0°到90°变化);a0为闸门全开时启闭机旋转中心到活塞杆与闸门连接处距离;b为闸门旋转中心到活塞杆与闸门连接处距离;c为启闭机旋转中心到闸门旋转中心的距离;β0为闸门全开时活塞杆与闸门连接处同闸门旋转中心的连线与启闭机旋转中心同闸门旋转中心的连线之间的夹角,此类参数均与启闭机布置尺寸有关。定义门位N=(90°-βi)/90°,即闸门运行角度βi=0°时,门位N=1。
研究模拟闸门活塞杆匀速运动180 s过程,活塞杆需经历初期加速及后期减速阶段,由模型试验统计初期加速时间为2 s,将活塞杆运动方式简化为1~2 s匀加速、2~178 s匀速、178~180 s匀减速三阶段。利用式(8)得到闸门角速度过程,给出控制闸门运动UDF。
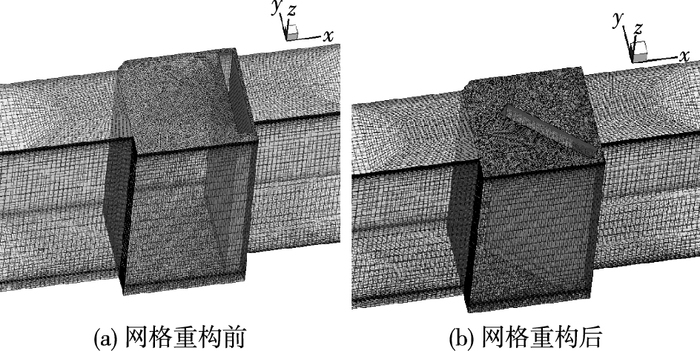
图 3给出闸门开启过程中网格重构前及重构后运动区域网格,网格质量重构良好,满足计算要求。
|
图 3 一字闸门开启过程网格对比 Figure 3 Comparison of grids for single-leaf gate |
验证淹没水深为30 m、门底间隙2.1 m,活塞杆匀速运动时长180 s门体开启及关闭过程所受动水阻力矩过程。
3.1 动水阻力矩验证一字闸门承受动水阻力矩Mz为水流作用力对门体旋转中心求矩,包括水压力阻力矩Mpz及黏滞力阻力矩Mvz。其中水流对门体运行过程阻力,主要为x方向水压力Fpx与黏滞力Fvx,y方向水压力Fpy与黏滞力Fvy。水流作用力[10]表示如下
| $\begin{array}{l} {F_{px}} = \int\limits_{{A_{\rm{s}}}} {{p_x}} {\rm{d}}S;{F_{py}} = \int\limits_{{A_{\rm{s}}}} {{p_y}} {\rm{d}}S;{F_{vx}} = \int\limits_{{A_{\rm{s}}}} {{\tau _x}} {\rm{d}}S;{F_{vy}} = \int\limits_{{A_{\rm{s}}}} {{\tau _y}} {\rm{d}}S\\ {M_z} = {M_{pz}} + {M_{vz}} = \int\limits_{{A_{\rm{s}}}} {{p_x}} (y - {y_0}){\rm{d}}s + \int\limits_{{A_{\rm{s}}}} {{p_y}} (x - {x_0}){\rm{d}}s\\ + \int\limits_{{A_{\rm{s}}}} {{\tau _x}} (y - {y_0}){\rm{d}}s + \int\limits_{{A_{\rm{s}}}} {{\tau _y}} (x - {x_0}){\rm{d}}s \end{array}$ | (9) |
式中:px,py分别为一字闸门任意表面上水压力在x,y方向上的分量;τx,τy分别为一字闸门任意表面上黏滞应力在x,y方向上的分量;As为一字闸门表面;(x0,y0)为一字闸门垂直旋转轴坐标,(x,y,z)为一字闸门门体表面任意一点坐标,动水阻力矩根据一字闸门门体网格采用数值积分求出。
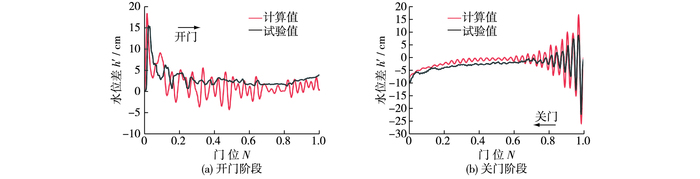
3.2 门前后波动水位差验证数学模型计算与物理模型试验在动水阻力矩量值、闸门前后水位波动及变化趋势方面吻合较好(见图 4和5),可以认为数值模拟方法正确,结果可信。

|
图 4 动水阻力矩数模计算值与物模实测值对比 Figure 4 Comparison between calculated and measured values of hydraulic torque |
|
图 5 门前后平均水位波动差数模计算值与物模实测值对比 Figure 5 Comparison between calculated and measured values of water level fluctuation |
通过数值模拟闸门活塞杆匀速开启180 s工况下流场情况,带门底间隙的一字闸门在启闭过程中具有明显的三维特性。
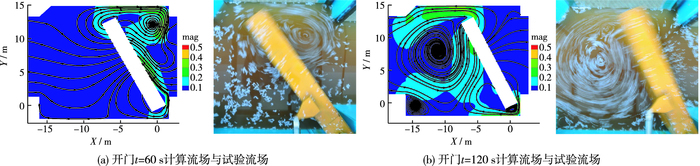
图 6和7分别给出了一字闸门开启过程水平表面及垂向流场的变化过程(mag表示投影在显示截面上流速的大小):对比计算及实测流场图可以发现,流态变化特性与模型试验观测到的水流流态一致。
|
图 6 一字闸门活塞杆匀速开启180 s过程表面流场变化(单位:m/s) Figure 6 Horizontal flow field past opening gate (unit: m/s) |

|
图 7 一字闸门活塞杆匀速开启180 s过程垂向流场变化(单位:m/s) Figure 7 Vertical flow field past opening gate (unit: m/s) |
开门初期,闸门推动水体,部分水体通过门底、门头及门尾部缝隙绕过闸门,垂向水流交换显著,绕流过流面小,水平流速大。随着门体开启,绕过门头的水流发生分离,在背离闸门运动方向面形成一个竖轴漩涡,漩涡尺寸随着门体靠近门库而逐渐变大,漩涡中心逐渐向门库侧移动。底部水体流过门体时与门底间隙发生分离,进而发展成横轴漩涡,并与竖轴漩涡相互作用,影响门后竖轴漩涡长度。闸门运动推动水体至全开位阶段,门库边界与门体共同作用,致使闸门门前水位壅高,水流受挤压向门底、门头及门尾处间隙流动,此时门前水流垂向速度向下,水平流速向门体门头及门尾两侧。然而受闸室内竖轴漩涡的影响,门后水流同样垂向流速向下,水平流速向门头及门尾两侧,阻碍各缝隙出口的水流交换,此时会在门底间隙处形成横向漩涡。受门库、门体边界及闸室漩涡的综合影响,门库内水流流动不畅产生振荡波动,形成动水阻力矩峰值。
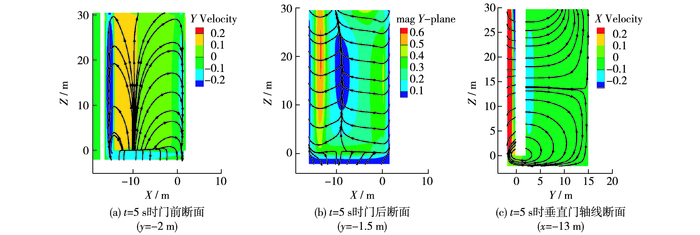
4.2 关门阶段图 8和9分别给出了一字闸门关闭过程水平表面及垂向流场的变化过程:闸门运动推动水体至全关位阶段,关门初闸门从门库位置开始推动水体,启动初期致使门库内水位下降,门前后面产生较大水位差,引起门前水流通过底部、门头及门尾位置处间隙向门内补水,门底形成横轴漩涡。补水水流在门后形成交汇,由于门库形式“窄而浅”且闸门门头处水流不畅,门库中往复振荡形成水面波动。随门体关闭,水流绕过门头发生分离,在背离闸门运动方向侧形成竖轴漩涡,门头离开门库瞬间漩涡迅速发展,漩涡尺寸随门体靠近全关位而逐渐变大,漩涡中心向全关位移动。门体、闸墙及门底门槛共同作用下,闸门门前水位壅高,水流受挤压向门底、门头及门尾处间隙流动,此时门前水流垂向速度向下,水平流速向门体门头及门尾两侧,受挤压水体通过门头处流动方向与开门过程中形成竖轴漩涡方向一致,水体沿闸墙流动并与漩涡汇合。通过门尾缝隙流向闸门另一侧水体运动方向与漩涡旋转方向相反,与漩涡充分能量交换后速度逐渐减小。

|
图 8 一字闸门活塞杆匀速关闭180 s表面流场变化(单位:m/s) Figure 8 Horizontal flow field past closing gate (unit: m/s) |
|
图 9 一字闸门活塞杆匀速关闭180 s过程垂向流场变化(单位:m/s) Figure 9 Vertical flow field past closing gate (unit: m/s) |
门底间隙的大小影响水流通过底部的通畅与否,绕流形成横轴漩涡影响竖轴漩涡的长度,门底间隙越大,竖轴漩涡长度越短,影响门体运行受力。通过数值计算获得不同门底间隙下一字闸门启闭过程动水阻力矩曲线(见图 10),并作不同门底间隙下各阶段阻力矩峰值散点图(见图 11)。
|
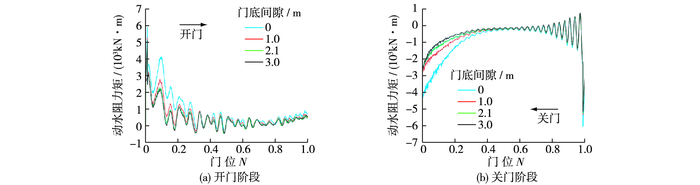
图 10 不同门底间隙情况下动水阻力矩计算曲线 Figure 10 Hydraulic torque with different gate clearances |
|
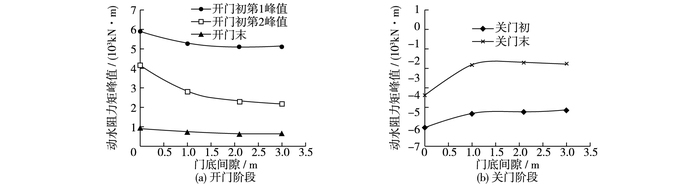
图 11 不同门底间隙下动水阻力矩峰值计算值 Figure 11 Variation of hydraulic torque peak values with different gate clearances |
由图 10可知,闸门启闭开始及末了都各有1个峰值,且开门初期还出现第2峰值,第1峰值发生在闸门启动瞬间,第2峰值发生在闸门门位0.1处。
一字闸门几个典型阶段的动水阻力矩峰值随门底间隙增大均有相应减小,门底间隙对闸门运行整个阶段的动水阻力矩均有影响。
开门阶段,门底间隙由0增加到2.1 m,开门初第1峰值与第2峰值及开门末动水阻力矩峰值分别下降13%,44%及33%,说明门底间隙对开门初第2峰值影响较大,主要由于闸门开门初期门头与闸墙距离很小,若门底间隙过小,在此阶段门前后水位差必然迅速增大,而第2峰值所在门位恰好为门头边缘与闸墙边界的距离由小开始增大的临界位置,门前水位在此门位之前将持续壅高,因此需合理设置门底间隙,避免开门初第2峰值出现。当门底间隙继续增大,阻力矩峰值降低不明显。
关门阶段,门底间隙由0增加到2.1 m,关门初及关门末阻力矩峰值分别下降13%和39%,说明关门末动水阻力矩峰值对门底间隙大小更为敏感。当门底间隙继续增大,关门阶段阻力矩增长不明显。
6 结语针对高水头船闸一字闸门建立三维数值模拟,通过建立二维平面网格(闸门运动区域为三角形非结构网格,其余为结构网格),纵向拉伸为三维棱柱体网格方式,较好地结合2.5D网格重构及弹性光顺动网格方法,减少计算网格数量、提高计算效率的同时,实现一字闸门启闭全过程三维流场模拟,计算结果与物理模型试验结果吻合良好,表明建立数值模型可靠,具有较高计算精度。
根据模拟结果,首次揭示一字闸门启闭过程流场变化规律,在门库等边界条件约束、水体绕过门头处分离产生的竖轴漩涡及绕过门体间隙分离形成的横轴漩涡综合影响,具有较强三维特性。
门底间隙大小影响动水阻力矩全过程,增大门底间隙可降低动水阻力矩峰值。较小的门底间隙会使一字闸门在开门过程门位0.1处产生阻力矩第2峰值,应予以避免。
| [1] |
李云, 徐新敏. 三峡永久船闸人字门液压启闭机运行方式优化试验研究[J]. 水利水运科学研究, 2000(1): 1-7. ( LI Yun, XU Xinmin. Study on operating manners of headstock gears of miter gates in Three-Gorge Ship Locks[J]. Journal of Nanjing Hydraulic Research Institute, 2000(1): 1-7. (in Chinese)) |
| [2] |
HIRT C W, NICHOLS B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of Computational Physics, 1981, 39(1): 201-225. DOI:10.1016/0021-9991(81)90145-5 |
| [3] |
SHIH T, LIOU W W, SHABBIR A, et al. A new k-ε eddy viscosity model for high Reynolds number turbulent flows[J]. Computers & Fluids, 1995, 24(3): 227-238. |
| [4] |
郑培喜. 船闸人字门动水阻力矩的数值计算研究[J]. 水利学报, 1992(12): 81-85. ( ZHENG Peixi. Numerical study on hydraulic torque of miter gates[J]. Journal of Hydraulic Engineering, 1992(12): 81-85. (in Chinese)) |
| [5] |
郑培喜. 带门底间隙人字门的动水阻力矩计算研究[J]. 力学与实践, 1992, 14(2): 22-25. ( ZHENG Peixi. Numerical study on hydraulic torque of miter gates with bottom clearance[J]. Mechanics in Engineering, 1992, 14(2): 22-25. (in Chinese)) |
| [6] |
Fluent Inc.Ansys Fluent 14.5 User's Guide[Z]. Lebanon, NH, 2011.
|
| [7] |
李鹏飞, 徐敏义, 王飞飞. 精通CFD动网格工程仿真与案例实战[M]. 北京: 人民邮电出版社, 2013. ( LI Pengfei, XU Mingyi, WANG Feifei. Proficient in engineering simulation with CFD dynamic mesh and cases for practice[M]. Beijing: Posts and Telecom Press, 2013. (in Chinese))
|
| [8] |
须清华, 张瑞凯. 通航建筑物应用基础硏究[M]. 北京: 中国水利水电出版社, 1999. ( XU Qinghua, ZHANG Ruikai. Fundamental study on application of navigation structure[M]. Beijing: China Water and Power Press, 1999. (in Chinese))
|
| [9] |
周衍柏. 理论力学教程[M]. 北京: 高等教育出版社, 1986. ( ZHOU Yanbai. Tutorial for theoretical mechanics[M]. Beijing: Higher Education Press, 1986. (in Chinese))
|
| [10] |
吴望一. 流体力学[M]. 北京: 北京大学出版社, 2004. ( WU Wangyi. Fluid mechanics[M]. Beijing: Peking University Press, 2004. (in Chinese))
|
 2017
2017 