2. 交通运输部天津水运工程科学研究院,天津 300456
随着我国内河水运交通量的持续增加,船闸通过能力相对航运过闸需求不足的矛盾愈发突出[1]。在不改变基础设施的情况下,优化交通组织能够高效节约地发挥作用[2],有利于提高船闸通过能力与服务质量。就船闸调度问题而言,进行交通建模与仿真是一种有效手段,需要考虑通过能力、延误和安全等多个相互联系与制约的目标[3-4],是一个复杂的多目标的不确定性组合优化问题[5]。国外现有的船闸交通建模主要基于标准化程度很高的船型(过闸船舶)[6-9],难以适用于国内复杂的非标准船型。针对船闸交通建模中关键的复杂船型的闸室排档问题[10],结合三峡-葛洲坝船闸通航调度理论问题,国内学者提出了一些实用的交通建模方法[11],为船闸运行仿真研究奠定了较好的基础。尽管以往在船闸仿真建模方面做了许多工作[12-15],但需要加强对仿真结果的验证与船闸运行状态的分析,充分掌握其交通规律,再现船舶过闸的时空变化,分析各种条件变化引起的船闸状态的改变,以利于优化交通组织方案,缩短船舶延误,定量预测其通过能力。本文在已有研究基础上,以湘江长沙枢纽双线船闸为例,基于Arena离散事件仿真平台[16]建立船闸交通仿真模型,并根据实际运行数据进行验证,预报该船闸在不同设计水平下的闸室利用率、船舶延误和通过能力等运行状态参数,通过对比船闸在不同船舶到达分布与调度策略下的运行状态,提出适用于不同工况的交通组织方案。
1 调度规则与算法 1.1 调度规则船闸调度与其优化目标、到达船舶和交通负荷等有关,往往难以直接建模求解。通常是先根据实践拟定某种调度规则,并设计相应的算法,通过仿真建模分析对应的船闸运行状态,最后比较优化目标而确定相对较优的方案。根据国内船闸的实际运行情况,船闸调度中的基本规则是先到先过和重点优先,故拟定基本调度规则:①过闸优先级按下列次序:危险品船>公务船>客船和鲜货船(载运鲜活货的货船)>普通货船等,其中,危险品船又分为运输固体危险品船与液体危险品船两大类,公务船指担任特殊任务的军事运输船等;②危险品船安排专闸通过,同类型危险品船可一同过闸,反之则不能同一闸通过;③同一优先级船舶采用先到先过。
为提高过闸效率,在基本调度规则基础上,针对同一优先级别船舶,注意大、小船协同,以闸室利用率最大为目标进行排挡优化,形成优化调度规则。当船闸将要或已经出现大量船舶积压时,采用应急调度规则,即在优化调度规则基础上,危险品船将不再优先和专闸通过,而是进入锚地等待,待危险品船舶数量满足一定条件时才允许集中过闸,但不同类型的危险品船仍不能同一闸通过。
1.2 调度算法图 1为基本调度规则的双线船闸单向调度算法。其中,危险品船不进入锚地,直接前往引航道内靠船墩等待过闸;其余船舶进入锚地等待。船舶排队算法的具体步骤为:①船舶进入锚地后按优先级及先后顺序形成待闸队列;②按顺序提取待闸队列中一批船舶进入排档模块;③按船舶长度指标(该方法排序可得到较大的闸室利用率)再次排序形成排档队列;④调用闸室排档算法,按顺序对排档队列中船舶进行排档,选取闸室利用率最大的一组为该闸次的排挡方案;⑤判断是否满足调度条件,若满足则进入闸室判别,否则继续等待来船;⑥如当前仅有唯一导航墙空闲,则直接前往该导航墙,否则判断能够较早形成当前方向过闸的导航墙;⑦如两导航墙在同一时刻均能过闸,则均衡两闸室通过量,选择当日通过量较小的并前往待闸;⑧下一闸次排档前根据锚地排队顺序补充船舶进入排档模块,然后重复③~⑦。
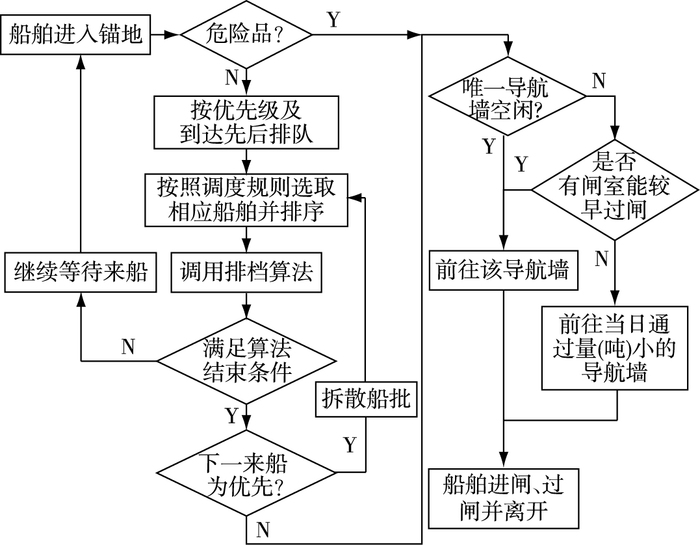
|
图 1 双线船闸单向调度算法流程 Figure 1 One-directional operation scheduling algorithm of shiplock |
每闸次调度结束条件有两种:一是锚地中尚有船舶,但没有合适的船舶能够进入闸室;二是锚地中没有船舶,考虑船闸运行成本和船舶延误时间,根据闸室利用率λ和已排档船舶等待时间来控制,具体判断条件是:①当λ<0.3时,本闸次最多等待60 min;②当0.3≤λ<0.6时,本闸次最多等待30 min;③当λ≥0.6时,本闸次最多等待15 min;若超过既定等待时间,锚地中仍无船舶,则立即调度该闸次。另外,应急调度规则中若满足λ≥0.50,即可安排集中过闸。
基于可排点的闸室排挡算法为:①将排档队列中首位船舶安排在闸室的(0,0)点上,将该船舶左下角坐标(x,y)赋值(0,0),将该船从队列移除;②将新产生的可排点放入原有的可排点队列中,并进行排序(先按x坐标升序排列,x相同时按y升序排列);③调用排档队列中首位船舶,将可排点队列队首的坐标赋给该船,若能通过约束检验,就把该船放在该点,对应的可排点从队列移除;反之则试探下一个可排点;若所有的可排点都放不下该船舶,就放弃该船舶,取队列中下一个船舶来试排;④重复步骤②~③直到排档队列为空或闸室排满为止,停止计算。具体算法流程图可参照文献[4]。
2 仿真建模 2.1 工程背景湘江为我国“一纵两横,两网十八线”高等级航道网中的“一线”,是连接长株潭沿江经济走廊与长江干线的水上交通要道。长沙枢纽是湘江干流九级开发中的最下游梯级,位于望城县境内的蔡家洲河段,是一座以改善航运和滨水环境为主,兼有供水、发电等综合效益的枢纽工程[4]。长沙枢纽建有双线2 000 t级船闸,闸室有效尺度280 m×34 m×4.5 m(长×宽×底槛水深),2012年9月建成并试通航运行。
2.2 仿真输入参数基于Arena离散事件仿真平台建立模型,范围从上游锚地至下游锚地,包括两个锚地、上下游引航道及靠船墩、两线船闸等。在仿真模型中,船舶到达规律与过闸服务时间是重要输入参数。其中,船舶到达规律包括一定时间间隔内到达的船舶数量及其属性(类型、吨位、总长、总宽等)。为简化问题,通常先将复杂的船型进行统计分类,选取代表船型及其对应比例(代表船型越多越接近实际情况),然后分析船舶到达数量的分布,按船型概率生成船舶。根据文献[4],选取16种船型作为仿真模型的代表船型。因缺乏系统的到船资料,在此不妨假定小时到船率服从泊松分布。
过闸服务时间不仅与灌泄水时间、闸门启闭时间等有关,还与船舶类型、船舶进出闸的速度与数量以及船员的操作熟练程度等有关。为简化问题,仿真模型中灌泄水时间、船舶进出闸速度等参数均看成常数,重点考虑过闸船舶艘数对一次过闸时间的影响;同时考虑两种工况,工况1考虑船闸在试运行期情况,船闸日运行19 h;工况2表示船闸经过一段运行后所达到的设计水平,船闸日运行21 h,具体参数取值参看文献[4]。此外,根据船闸的通航水流条件,一线和二线船闸运行时不能同时进行灌水或泄水操作。
假定船闸具有良好运行状态,不考虑船闸运营中因各种原因造成的停航,忽略航道、水文、气象等客观因素对船闸运行的影响。为节约模型运行时间,同时减小随机性带来的误差,设置仿真运行时间为30 d,各工况重复模拟次数为10次。
3 运行状态与通过能力分析 3.1 模型验证根据实际情况,试运行初期设备故障较多,且船长对于船舶过闸有一个适应过程,为减小延误并提高船闸的通过能力,工况1采用应急调度规则;工况2下船闸正常运行,可采用优化调度规则。为率定并验证该仿真模型,收集了该船闸试运行期第3个月(2012年12月)以及运行10个月后(2013年7月,详见文献[17])的月运行资料。其中,2012年12月过闸船舶的平均吨位为772 t/艘,双向流量V=179艘/d;2013年7月的双向流量V=200艘/d。两次实际运行情况分别与工况1和工况2的运行条件接近,用来验证该模型,结果详见表 1。仿真模型计算得到的各项主要参数与实际运行数据一致,相对误差均不超过10%。进一步,图 2(a)绘出了工况1条件下仿真与实际的闸室利用率分布,两者吻合良好,除了仿真的闸室利用率在0.3~0.5区间的比例略高。由此可见,模型验证情况良好,证明了仿真模型的可靠性,故可用来分析船闸的运行状态与通过能力。
| 表 1 船闸交通仿真结果与实际运行数据比较 Table 1 Comparison between simulated result and actual operation data |

|
图 2 工况1闸室利用率统计 Figure 2 Distribution of chamber utilization under working condition 1 |
表 2为模型验证时仿真运行1个月的各参数值。平均延误是指船舶从进入锚地到离开锚地(准备过闸)为止的这段时间。排队长度指停泊在锚地的船舶数量,不包括准备过闸的船舶。交通负荷ρ(ρ=V/C,服务率C=m/T)反映船闸服务系统的繁忙程度;当ρ<1时,该排队系统稳定;当ρ>1时,该系统不稳定,意味着系统延误随着时间的推移将越来越大。
| 表 2 船闸在不同条件下运行1个月的状态参数(V=179艘/d) Table 2 Shiplock performance parameters under different conditions in a month |
从表 2可见,工况1下船舶的平均延误约为2.58 h(约2闸次),平均延误船舶量约2.1艘,交通负荷约0.87,闸室利用率亦达到国内其他船闸的多年平均值[1],反映出工况1下采用应急调度时,尽管交通负荷较大但船闸运行状态尚可。同工况1相比,工况2减小了一次过闸时间,增加了过闸次数,将船舶平均延误缩短至1.17 h,不过,也使得平均闸室利用率和一次过闸平均艘数有所降低。仿真结果表明,每个闸次的船舶艘数越多,则一次过闸时间就长,平均延误就长。在实际调度中,可根据船闸状态和过闸交通需求,合理进行交通组织调度,在船闸通过能力(过闸船舶总吨位)与船舶平均延误之间取得平衡。
需要说明的是,当交通需求量较小时,由于到达船舶的随机性,为兼顾船闸运行成本和船舶延误时间,闸室利用率并不能显著提高。若考虑交通需求量大的情况,将日均流量增加1倍(即V=358艘/d),其他条件同工况1,仿真得到的闸室利用率为0.7~0.8的所占比例可达62%,如图 1(b)。表明交通需求较大时,积压的船舶有利于优化排挡,同时采用应急调度规则降低危险品船的优先级,能够显著提高闸室利用率,但要注意设置临时专用锚地并加强管理,确保船舶过闸安全;同时亦需要组织协调,避免可能造成危险品船舶待闸时间过长。
3.3 船舶到达的影响船舶到达的种类、数量和规律与船闸的运行状态有着直接关系。为分析船舶到达分布的影响,在工况1相同调度规则下,仿真计算了船舶按均匀到达时船闸的运行指标,详见表 3。对比工况1船舶按泊松分布到达时的结果(表 2),在交通需求相同(V=179艘/d)的情况下,船舶到达分布对过闸船舶总量没有影响,但会影响船闸的服务质量。当船舶到达从泊松分布变为均匀分布时,一次过闸平均吨位从4 871 t增加到5 157 t,平均排队长度从2.1艘减小到1.4艘;船舶平均延误从2.6 h减少到2.0 h,每月可减少延误3 222 h。仿真结果表明,降低船舶到达的随机性,有助于提高船闸的闸室利用率和通过能力,减小船舶平均延误和平均排队长度,经济效益显著。在运行实践中,可通过航运企业的配合进行有计划地安排,提前组织船舶过闸,降低船舶延误费用。
| 表 3 工况1船闸应急调度运行1个月的运行状态参数(船舶均匀到达) Table 3 Shiplock performance parameters of emergency scheduling under working condition 1 in a month |
船闸的通过能力不仅与其规模和技术指标有关,还与船型、交通负荷和调度方式等因素有关。考虑排队系统的稳定性,认为当该船闸的交通负荷无限接近1但小于1时,对应的通过能力是该条件下船闸的最大通过能力,由此可根据不同交通负荷预先选取最优船闸调度方案,避免出现船闸滞航现象。仍以工况1为例,假设船舶到达符合泊松分布,仿真计算得到基本调度规则、优化调度规则及应急调度规则对应的船闸最大日通过量分别为185艘/d, 190艘/d, 215艘/d。综合考虑各调度规则特点,以减小系统船舶延误为目标,兼顾公平,工况1条件下,到船率V≤185艘/d时,可采用基本调度规则进行调度;当185艘/d<V≤190艘/d时,可采用优化调度规则;当190艘/d<V≤215艘/d时,宜采用应急调度规则;当V>215艘/d时,船闸将会有大量船舶积压。
另外,根据船闸的设计条件(运量不均衡系数1.3,装载系数0.8,船舶平均吨位956 t/艘,工况2),暂不考虑船舶的标准化和大型化,以优化调度规则为例,仿真计算得到不同运量时船闸的运行状态参数,见表 4。图 3绘出了工况2不同调度规则下平均排队长度与通过能力的关系曲线。可以看出,当排队长度较小时(通常小于5艘),船闸通过能力随着排队长度增加而迅速增加,然后缓慢逼近一条渐近线。表明随着船闸系统的延误无限增加,船闸的通过能力也不会显著增加。根据交通负荷推断,在设计条件下长沙枢纽船闸在基本调度规则、优化调度规则及应急调度规则时船闸最大单向通过能力分别约为3 076万t,3 378万t和3 764万t,超过该船闸2013年、2014年2 934万t和4 971万t的实际双向过闸货运量,但小于原设计的4 800万t的单向年通过能力。
| 表 4 工况2时不同过闸运量条件下的船闸运行状态参数(优化调度规则) Table 4 Shiplock performance parameters with optimal operation under different throughput conditions of working condition 2 |
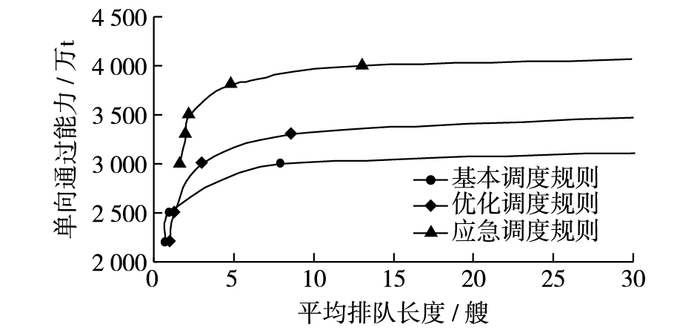
|
图 3 平均排队长度与单向通过能力的关系 Figure 3 Relationships between average queue length and one-directional throughput capacity of shiplock |
(1) 将船闸视为单个或多个服务窗口的排队系统,基于Arena离散事件仿真平台进行交通建模与仿真,可再现船舶过闸的时空变化及其运行状态,并通过实际数据能够验证模型的可靠性。通过分析仿真模型输出结果(船闸运行状态参数),有助于充分掌握船闸系统的交通规律。
(2) 仿真结果表明,只有提高每个闸次的闸室利用率,才能有效增加船闸的通过能力;不过,每个闸次的船舶艘数越多,一次过闸时间就长,平均延误就长。运行实践中,可根据船闸状态和过闸交通需求,合理进行交通调度,如危险品集中过闸、航运企业有计划过闸等,在保障过闸安全的前提下协调船闸通过能力与船舶延误之间的关系。
(3) 考虑排队系统的稳定性,当船闸的交通负荷无限接近1且小于1时,对应的通过能力是船闸的最大通过能力。据此可分析不同设计水平下的船闸最大通过能力,或是根据不同交通负荷预先优选调度方案,以便提高船闸的通过能力与服务质量。
| [1] |
廖鹏, 张玮. 船闸一次过闸平均吨位计算模型[J]. 东南大学学报(自然科学版), 2010, 40(1): 207-212. ( LIAO Peng, ZHANG Wei. Analytical model for average lockage tonnage of waterway locks[J]. Journal of Southeast University(Natural Science Edition), 2010, 40(1): 207-212. (in Chinese)) |
| [2] |
王炜, 过秀成. 交通工程学[M]. 2版. 南京: 东南大学出版社, 2011. ( WANG Wei, GUO Xiucheng. Traffic engineering[M]. 2nd ed. Nanjing: Southeast University Press, 2011. (in Chinese))
|
| [3] |
庞雪松, 潘荣友, 廖鹏. 提高长洲枢纽现有船闸通过能力对策研究[J]. 水运工程, 2011(4): 114-119, 125. ( PANG Xuesong, PAN Rongyou, LIAO Peng. On improvement of navigation lock capacity at Changzhou hydro-complex[J]. Port & Waterway Engineering, 2011(4): 114-119, 125. (in Chinese)) |
| [4] |
蒋明锋, 张明, 廖鹏, 等. 长沙枢纽船闸运行初期的通过能力研究[J]. 水道港口, 2013, 34(4): 359-363. ( JIANG Mingfeng, ZHANG Ming, LIAO Peng, et al. Study on recent lock capacity of Changsha hydro-junction[J]. Journal of Waterway and Harbor, 2013, 34(4): 359-363. (in Chinese)) |
| [5] |
VERSTICHEL J, CAUSMAECKER P, SPIEKSMA F, et al. The generalized lock scheduling problem: An exact approach[J]. Transportation Research Part E: Logistics and Transportation Review, 2014, 65(2): 16-34. |
| [6] |
DAI M D M, SCHONFELD P. Metamodels for estimating waterway delays through series of queues[J]. Transportation Research: Part B, 1998, 32(1): 1-19. DOI:10.1016/S0191-2615(97)00003-9 |
| [7] |
TING C J, SCHONFELD P. Control alternatives at a waterway lock[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2001, 127(2): 89-96. DOI:10.1061/(ASCE)0733-950X(2001)127:2(89) |
| [8] |
CORTÉS P, MUÑUZURI J, GUADIX J. Simulation of freight traffic in the Seville inland port[J]. Simulation Modelling Practice & Theory, 2007, 15(3): 256-271. |
| [9] |
SMITH L D, SWEENEY D C Ⅱ, CAMPBELL J f. Simulation of alternative approaches to relieving congestion at locks in a river transportation system[J]. Journal of the Operational Research Society, 2009, 60: 519-533. DOI:10.1057/palgrave.jors.2602587 |
| [10] |
VERSTICHEL J, CAUSMAECKER P, VANDEN BERGHE G. An improved best-fit heuristic for the orthogonal strip packing problem[J]. International Transactions in Operational Research, 2013, 20(5): 711-730. DOI:10.1111/itor.12030 |
| [11] |
齐欢, 肖恒辉, 张晓盼. 三峡-葛洲坝通航调度的理论研究与工程实践[M]. 北京: 科学出版社, 2010. ( QI Huan, XIAO Henghui, ZHANG Xiaopan. The theory research and engineering practice for the co-scheduling of the Three Gorges dam and the Gezhouba dam[M]. Beijing: Science Press, 2010. (in Chinese))
|
| [12] |
朱顺应, 朱凯, 王丽铮. 基于Arena的三峡枢纽运输系统仿真模型[J]. 水运工程, 2011(2): 40-44. ( ZHU Shunying, ZHU Kai, WANG Lizheng. A simulation model based on Arena for the transportation system of the Three Gorges region[J]. Port & Waterway Engineering, 2011(2): 40-44. (in Chinese)) |
| [13] |
商剑平, 吴澎, 唐颖. 基于计算机仿真的船闸联合调度方案研究[J]. 水运工程, 2011(9): 199-204. ( SHANG Jianping, WU Peng, TANG Ying. On multiple-lane lock's joint scheduling plan based on computer simulation[J]. Port & Waterway Engineering, 2011(9): 199-204. (in Chinese)) |
| [14] |
李楠, 李桂华, 尹剑平. 湘江船闸的过闸调度算法研究[J]. 水运工程, 2013(3): 171-175. ( LI Nan, LI Guihua, YIN Jianping. Scheduling algorithm for Xiang River lock chamber[J]. Port & Waterway Engineering, 2013(3): 171-175. (in Chinese)) |
| [15] |
柯姜岑, 甘露, 程超. 基于元胞自动机的船舶过闸运输组织仿真[J]. 水运工程, 2013(1): 123-129. ( KE Jiangcen, GAN Lu, CHENG Chao. Simulation of ship lock organization mode with cellular automata[J]. Port & Waterway Engineering, 2013(1): 123-129. (in Chinese)) |
| [16] |
KELTON W D. Simulation with Arena[M]. Columbus: The McGraw-Hill Companies, 2002.
|
| [17] |
王伟凡. 浅析长沙枢纽船闸投运初期提升通过能力的措施[J]. 湖南交通科技, 2014, 40(2): 171-173. ( WANG Weifan. Measures to improve the navigation lock capacity during the initial operation of Changsha hydro-complex[J]. Hunan Communication Science and Technology, 2014, 40(2): 171-173. (in Chinese)) |
2. Tianjin Research Institute of Water Transport Engineering, Ministry of Transport, Tianjin 300456, China
 2017
2017 
