2. 聊城大学 建筑工程学院,山东 聊城 252059
由高桩码头破坏形式可知,桩-土相互作用对高桩码头抗震性能有重大影响。桩-土相互作用可分为惯性作用和运动作用,惯性作用与上部结构的惯性力有关,运动作用与地震引起的地基变形有关[1],图 1为高桩码头中惯性作用和运动作用的示意。
|
图 1 作用在桩上的惯性作用和运动作用 Figure 1 Effects of inertial and kinematic forces on piles |
对于典型的梁板式和无梁板式高桩码头,惯性作用趋于在桩身靠上的部分引起最大弯矩和塑性铰,而运动作用趋于在桩身靠下的部分引起最大弯矩和塑性铰,如图 2所示[2]。通常,两种作用引起的桩身最大弯矩位置相距足够远以至于可忽略弯矩叠加效应,另外两种作用引起最大弯矩的时刻亦不相同,所以对于典型的梁板式和无梁板式高桩码头,在设计中可将惯性作用和运动作用分开考虑,但对于其他类型的码头应根据具体情况具体分析[3]。

|
图 2 由惯性作用和运动作用引起的塑性铰 Figure 2 Plastic hinge formation due to inertial and kinematic loading |
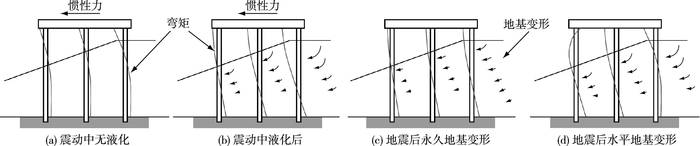
在设计中,专题Ⅰ中所述的非线性静力Pushover分析常被用于惯性作用的评估。在非线性静力分析中,一般用由p-y曲线确定的土弹簧模拟桩周土,弹簧一端与桩节点连接,另一端固定,即忽略岸坡的变形,通常地面以下10倍桩径范围内的土体对码头惯性反应起控制作用[4]。由专题Ⅰ可知,在基于位移的高桩码头抗震设计中,在验算码头位移能力是否满足抗震性能要求后应进行运动作用的评估,评估中应确定地基水平变形是否在有限范围内以保证桩的性能(材料应变)满足规定的性能要求(规范中的应变限值),图 3为POLB和POLA中运动作用的评估流程,其中OLE,CLE和DE为标准采用的3个地震动水准,即运营水平地震、偶遇水平地震和设计水平地震。

|
图 3 运动作用评估流程 Figure 3 Flow chart for evaluation of kinematic loading |
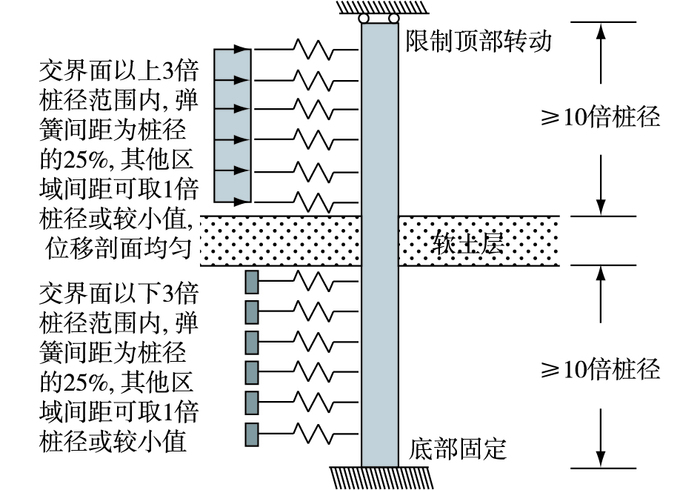
在图 3中,步骤①中的Newmark滑块位移计算一般根据经验图表或公式完成,对于OLE和CLE变形,POLB和POLA均给出了相应的图表,具体可参考文献[5]和[6],对于DE变形,可参考文献[7]中的经验公式。文献[7]中提出的Newmark滑块位移计算式针对的是美国各地区,选取的地震波也是美国各地曾发生过的地震,主要为美国工程设计服务,另外未对场地做出明确的区分。其他研究者[8-9]也提出了多个Newmark滑块位移计算公式,但都未对场地做出划分,将其直接用于我国码头岸坡变形的计算并不合适,故高树飞等[10]利用拟合于我国水运工程抗震设计规范反应谱的人工地震动得到了适合于规范不同场地的滑块位移计算公式。步骤③中进行桩Pushover分析的模型如图 4所示,其中桩“销”效应(Pile Pinning Effect)指桩对岸坡稳定的有利作用,这一步实际上是一个迭代过程,具体见文献[11]和[12]。桩-土动力相互作用分析可采用有限元法或有限差分法,至少进行二维分析。由此可见,规范中尽量通过简单的验算避免进行复杂的桩-土动力相互作用分析,因为桩-土动力相互作用分析的影响因素较多,计算较为复杂,耗时较长,不确定性因素较多。
|
图 4 滑动层模型 Figure 4 Sliding layer model |
如图 3所示,Newmark滑块位移法已用于高桩码头岸坡变形的计算。研究[13]表明,在考虑土体强度退化和桩“销”效应的前提下,该方法可以较好地预测高桩码头的岸坡变形;一般来说,在不考虑桩的作用时,会高估变形,反之,低估变形;当使用平均值加1倍标准差的孔压时,估计的变形比较准确。使用Newmark滑块位移法的难点在于准确预测孔压并选取具有代表性的加速度时程,试验研究表明[14],预测值与试验值存在较大差距,故对Newmark滑块位移法得到的高桩码头岸坡变形仍应慎重使用。
2 p-y曲线由专题Ⅰ可知在高桩码头桩-土相互作用分析中,非线性地基上的Winkler梁模型(Beam on Non-linear Winkler Foundation)使用较为广泛。在这一模型中,土体由p-y曲线确定的土弹簧代替,因而合理确定土的p-y曲线对模型计算结果的准确性有重要影响。
2.1 高桩码头中常用的p-y曲线在高桩码头静/动力分析中,规范中常用的软黏土和砂土的p-y曲线分别为Matlock[15]和O'Neill[16]的研究成果,被美国石油协会规范API RP 2A-WSD[17]所采用,我国港口工程桩基规范[18]也采用了该曲线。对于软黏土和砂土,其他学者也提出多种p-y曲线,如Reese等[19],虽未被规范采纳,但在工程中仍得到一定应用。对于硬黏土,规范未给出建议曲线,对于地下水位以上和以下的硬黏土的p-y曲线,可分别参考文献[20]和[21]。
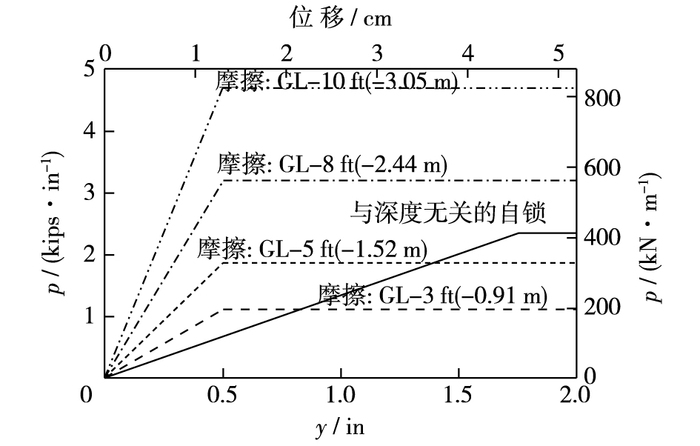
在高桩码头中,通常会设置块石护坡和抛石棱体,对于桩在砾石和块石中的p-y曲线研究很少,一般在缺乏更多详细信息的情况下,可考虑使用砂土的p-y曲线。在美国洛杉矶港,常采用图 5[22]所示的p-y曲线,该曲线是基于现场桩基荷载试验得到的,图中“GL”指地面。经研究认为图 5中的p-y曲线低估了桩侧土抗力,但准确地估计了桩身转角;认为桩在抛石中的土抗力可分为与应力水平有关和与应力水平无关的两个分量,其中与应力水平有关的土抗力可定义为与颗粒接触面平行的“摩擦”作用,即图 5中的土抗力,与应力水平无关的土抗力可定义为与接触面垂直的“自锁”作用。通过试验反算得到的与深度无关的“自锁”抗力如图 6所示,Kawamata[23]还计算了由“自锁”引起的拟黏聚力的大小(56~84 kPa),并通过计算证明了其假设的合理性。Diaz等[24]首先建议用拟黏聚力考虑由颗粒间的自锁和运动产生的额外土抗力,McCullough等[25]利用离心模型试验反算确定抛石的拟黏聚力为15 kPa,明显小于Kawamata的研究结果,Kawamata认为差异可能来源于试验材料的不同和尺寸效应。

|
图 5 码头设计中常用的抛石p-y曲线 Figure 5 p-y curves of rockfill typically used for wharf design |
|
图 6 摩擦和与深度无关的自锁抗力 Figure 6 Reaction of friction and depth independent interlocking |
规范中建议的p-y曲线均针对均匀单一土层,而在港口工程中,岸坡往往由多层土构成,如何应用p-y曲线是一个令设计人员感到困难的问题。有人采取对计算点以上土体物理力学参数进行加权平均的方法,或者直接认为计算点以上土层性质与计算点土层性质相同,这些近似处理方法难免会产生误差。金伟良等[26]基于Mohr-Coulomb破坏准则和Rankin理论对Matlock[15]和Reese等[19]分别提出的软黏土和砂土极限抗力表达式进行了修正,并考虑了成层土的影响,提出了多层土中桩侧极限土抗力表达式。较为常用的处理多层土的方法是Georgiadis[27]提出的方法,假定计算点以上土层的性质与计算点所在土层相同,并通过一个“等效厚度”计算桩侧极限土抗力,包括计算点所在土层性质的上部土层的等效厚度H1*可按下式计算:
| $\smallint _0^{{H_1}}{p_{u1}}\left( H \right){\rm{d}}H = \smallint _0^{{H_{{1^*}}}}{p_{u2}}\left( H \right){\rm{d}}H$ | (1) |
式中:pu1(H)为计算点以上土层的桩侧极限土抗力;pu2(H)为计算点所在土层的桩侧极限土抗力;H为地面以下深度;H1为计算点以上土层实际厚度。
2.3 p-y曲线的上限和下限由于岸坡块石特性、岸坡施工方法、岸坡倾斜和在结构设计中对p-y曲线的简化(即线性化,双线性化,三折线化)等因素存在的不确定性,设计中确定的p-y曲线也存在很大的不确定性,因此在进行上部结构惯性反应分析时考虑p-y曲线的上限和下限以保证计算结果可以适应p-y曲线潜在的变化[4]。在POLB和POLA中,对于土弹簧的荷载的上限和下限的p-乘子(p-multiplier)mp分别取2.0和0.3。POLB和POLA中mp的取值下限比较保守,而上限则不太保守[28];上限和下限取值对于岸坡坡度在1:(1.50~1.75)范围内是合适的,其他情况应具体问题具体分析[29]。
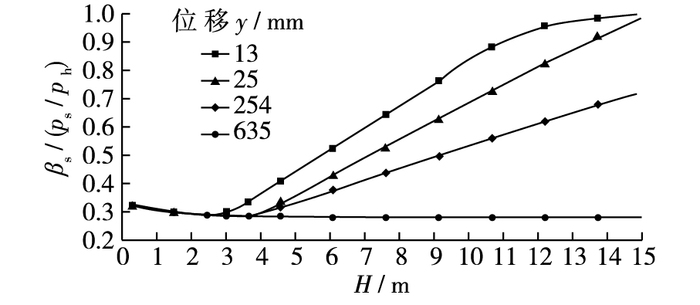
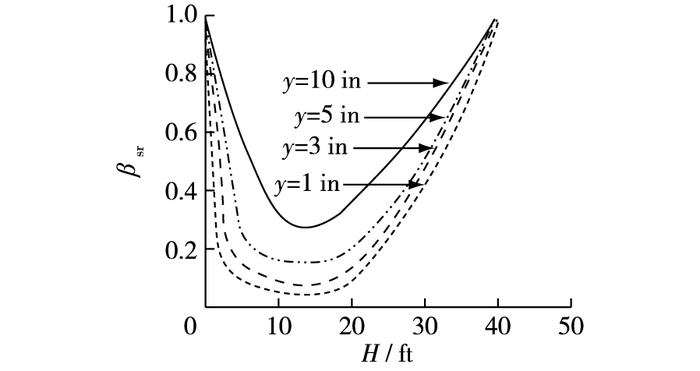
2.4 岸坡坡度的影响由于规范建议的p-y曲线都是针对水平地面,而高桩码头的岸坡通常是倾斜的,应考虑岸坡坡度对p-y曲线的影响,即上坡向和下坡向土弹簧的强度和刚度存在差异。McCullough等[25]通过对埋置于坡度为1:1.5的砂土(有效内摩擦角φ=45°,总重度γ=20.4kN/m3和地基反力模量k=24 430kN/m3)岸坡中的桩(610 mm)研究发现,下坡向和水平的p-y曲线存在如图 7所示的关系,图中β为倾斜地面中抗力与水平地面中抗力的比值,由图 7可知βs与深度和位移y有关。Chen和Martin[30]研究了黏聚力为30 kPa,内摩擦角为20°的土和直径为1 m的桩,得到坡度为1:1.5的岸坡坡顶地面处的βs为0.43。Mezazigh等[31]通过离心模型试验研究了倾斜岸坡(试验中桩距离岸坡的距离不同,桩不在岸坡内,而在水平地面内)对桩水平承载性状的影响,采用相对较缓的坡度(1:2和1:1.5),对于1:1.5的岸坡,由其给出的计算式得到的坡顶地面处的βs为0.33。Diaz等[24]建议采用下式计算βs:
|
图 7 下坡向修正系数βs Figure 7 Downslope modification factor βs |
| ${\beta _{\rm{s}}} = \frac{{{K_{{\rm{ps}}}} - {K_{{\rm{as}}}}}}{{{K_{\rm{p}}} - {K_{\rm{a}}}}}$ | (2) |
式中:Kps为库仑被动土压力系数(直墙,填土倾斜);Kas为库仑主动土压力系数(直墙,填土倾斜);Kp为库仑被动土压力系数(直墙,填土水平);Ka为库仑主动土压力系数(直墙,填土水平)。对于抛石岸坡,Diaz等给出了如图 8的修正系数βsr=psr/p,psr为试验条件下岸坡抛石的侧向土抗力,p为Reese等[19]提出的水平地面上砂土的土抗力。对于上坡向p-y曲线,可以直接取水平地面下的p-y曲线。
|
图 8 下坡向修正系数βsr Figure 8 Downslope modification factor βsr |
ASCE/COPRI 61-14[29]认为虽然上坡向和下坡向的土弹簧的特性存在差异,但是对高桩码头而言,当考虑桩在坡面以下一定深度时向相反的方向运动,而且在两个方向上刚度的相对差异随着深度而减小时,岸坡倾斜的影响是减弱的。因此,对于桩的整个埋置深度内使用上坡向土弹簧不合适。然而,由于缺少更多的研究,建议在分析中对于上坡向和下坡向的刚度和强度使用相同的值,而且这些值会随着上限和下限值的变化而不同。已有的研究表明,岸坡倾斜对p-y曲线有一定影响,但考虑到分析中考虑了上限和下限,可以在设计中直接采用水平地面下的p-y曲线,也可按照前述研究者的成果进行修正。
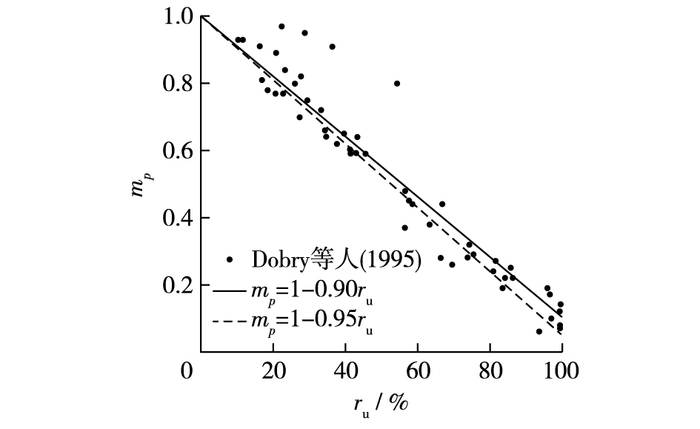
2.5 液化土中的p-y曲线在地震作用下,松散的饱和砂土易发生液化,一旦发生液化,桩-土相互作用将变得非常复杂,正如专题I中所示的POLB和POLA中运动作用评估过程,尽量避免进行复杂的考虑液化的桩-土动力相互作用分析,因而这两个标准也未给出建议使用的液化土中的p-y曲线。将传统的p-y曲线不经任何修正直接用于液化土的地震反应分析是不合适的[32],目前已开展了大量针对液化土中p-y曲线的研究。Wilson等[33]首次通过对离心模型试验反算得到了液化砂土的p-y曲线,结果表明液化砂土的p-y曲线与液化砂土的应力-应变的趋势一致,许多研究者也开展了大量的理论和试验研究,提出了一些液化土中的p-y曲线计算方法,如Boulanger等[34]。在实践中,最常用的解决方法是对土抗力p进行折减得到液化土中的p-y曲线,折减系数一般称为p-乘子(p-multiplier)mp。图 9[35]给出了Brandenberg[36]和日本建筑学会(AIJ)[37]建议的mp和修正的标准贯入击数(N1)60cs之间的关系,图中黑色的粗线为美国南卡罗纳州交通厅的《岩土设计手册》[35]建议采用的曲线,图中z为地面以下的深度,另外,Dobry等[38]通过离心模型试验得出mp随超孔压比ru呈线性变化,如图 10所示。

|
图 9 液化砂土的p-乘子与修正标准贯入击数的关系 Figure 9 Relationships between p-multiplier and corrected SPT blow counts for liquefied sand |
|
图 10 液化砂土的p-乘子与超孔压比的关系 Figure 10 Relationships between p-multiplier and excessive pore pressure ratio for liquefied sand |
在桩基工程中,常将桩模拟成嵌固于地面以下一定深度而无土体支撑,这一深度常被称为等效嵌固深度(Equivalent depth to fixity)。等效嵌固深度的计算基于同一水平力下等效悬臂桩与实际埋入土中的弹性桩的桩顶位移相同的原则确定,很多研究者开展了大量研究,如Davisson和Robinson[39]、张宗言[40]、Chen[41]和Budek等[42]。其中Davisson和Robinson的公式应用较广,已被美国国家公路与运输协会(AASHTO)《桥梁荷载与抗力系数设计规范》[43]采纳,等效嵌固深度的计算式如下:
| ${L_{\rm{f}}}{\rm{ = }}\left\{ {\begin{array}{*{20}{l}} {1.4\sqrt {{E_{\rm{p}}}{I_{\rm{p}}}/{E_{\rm{s}}}} \left( {黏土} \right)}\\ {1.8\sqrt {{E_{\rm{p}}}{I_{\rm{p}}}/{n_{\rm{h}}}} \left( {砂土} \right)} \end{array}} \right.$ | (3) |
式中:Ep为桩材料的弹性模量(MPa);Ip为桩截面惯性矩(mm4);Es为黏土的土模量,可参考规范确定,取为67Su,Su为黏土的不排水抗剪强度(MPa);为土模量随深度增长的比例系数(MPa/mm),可按规范确定。式(3)不区分桩顶固定或铰接,且适用于单一土层;对于多层土,应将多层土转化为等效的单一土层。
张宗言提出的计算式为我国《港口工程桩基规范》(JTS-167-4-2012)[18]所采用,形式如下:
| ${L_{\rm{f}}} = \eta T$ | (4) |
式中:η为系数,取1.8~2.2,桩顶铰接或桩的自由长度较大时取较小值,桩顶无转动或桩的自由长度较小时取较大值;T为桩的相对刚度特征值(m),按下式计算:
| $T = \sqrt[5]{{{E_{\rm{p}}}{I_{\rm{p}}}/(m{b_0})}}$ | (5) |
式中:m为桩侧地基土的水平抗力系数随深度增长的比例系数(N/mm4),根据《港口工程桩基规范》选取,b0为桩的换算宽度(mm)。我国《高桩码头设计与施工规范》[44]规定,码头下面设有抛石棱体,计算桩水平承载力和垂直承载力时,各桩的假想地表面可取码头前沿泥面与实际斜坡面交点的1/2处。桩的自由长度为桩台面板下表面到假想地表面的深度。
Chen[41]分别针对水平刚度、弯曲和屈曲提出了嵌固点的计算式,并考虑桩顶的约束条件,由于其计算式较为复杂,未能得到广泛使用。Budek等利用Winkler地基上的梁模型确定了桩顶自由和桩顶固定两种情况下的等效嵌固点深度,以图的形式给出,为国际航运协会《港口结构抗震设计指南》[45]所采用,其考虑了桩的自由长度Lu以及桩土间相对刚度的影响。
另外,美国统一设施准则《沿岸水工建筑物通则》(UFC4-151-10)[46]不通过计算确定桩的嵌固深度,而是根据土的类别和桩的刚度直接进行了规定。在软黏土中,当桩的刚度EpIp≤10×109lb-in2(1lb-in2=2 869.81 N·mm2)时,Lf取3.05 m;当桩的EpIp>10×109lb-in2时,Lf取3.66 m。在松散的颗粒土和中等黏性土中,桩的刚度EpIp≤10×109lb-in2时,Lf取2.44 m;桩的刚度EpIp>10×109lb-in2时,Lf取3.05 m。
日本《港湾设施技术标准与解说》[47]规定,桩的假想嵌固点可取假想地表面下1/βf处,βf按下式计算:
| ${\beta _{\rm{f}}} = \sqrt[4]{{{k_{{\rm{CH}}}}D/(4{E_{\rm{p}}}{I_{\rm{p}}})}}$ | (6) |
式中:βf为桩假想嵌固点参数(m-1);D为桩直径(m);kCH为桩的水平地基反力系数(N/mm3)。日本规范假想地面的确定方法与中国规范不同,具体确定方法见文献[47]。在计算上部结构惯性力时,需采用假想嵌固点处的地震动,此处地震动需经过场地反应分析获得,可参考文献[48]。
由此可见,不同国家规范中桩嵌固深度的确定方法并不相同,假想嵌固深度的确定受到桩顶条件和地基土条件的影响,变化范围约为2~15倍桩径[4]。另外,还可以近似取5倍桩径作为等效嵌固深度进行初步计算[45]。前述等效嵌固点都是在静力条件下进行确定的,研究[49]表明,在动力条件下等效嵌固深度会增大。Ayothiraman等[49]研究了动力条件下桩在黏土中的嵌固深度,可以用于动力下桩基动力反应的计算。
总而言之,虽然假想等效嵌固点法可以较为准确地预测弹性刚度、位移和周期,但高估了土中桩的弯矩,不能准确预测桩顶和土内塑性铰的内力[4],其在基于力的抗震设计方法中仍被广泛使用,而在基于位移的抗震设计方法中却被限制使用,一般用于初步设计中。在基于位移的设计方法中,在桩坐落于浅层基岩上或土的反应不显著的情况下,允许使用等效嵌固深度[29]。
4 动力分析由图 3可知,对于POLB和POLA,当初步分析岸坡变形不满足要求时,需进行详细的桩-土动力相互作用分析。PIANC规定,对于性能等级为A和S的结构应采用动力分析评估其地震反应。我国《水运工程抗震设计规范》(JTS 146—2012)规定,在7度区码头高度大于35 m或在8度区码头高度大于30 m时,应考虑桩-土相互作用,采用等效线性或非线性时程分析法求解码头结构的地震应力和加速度反应。可见,考虑桩-土相互作用的高桩码头动力分析是评估码头地震反应的重要方法之一,但高桩码头动力分析相较于其他方法较为复杂。另外,为保证动力时程分析结果的合理性,POLB规定,应将动力时程分析结果与其他方法的结果进行对比,且误差不应大于20%,MOTEMS亦有类似规定。
4.1 方法与模型近年来,关于桩-土动力相互作用的研究,已提出很多模型和方法。从求解域上,可分为直接法(整体法)和子结构法。直接法,顾名思义,即在一步内同时分析土体和结构及其相互作用,需要很大的计算量。子结构法将土和结构分开建模,将土体的反应施加在结构上,最终得到结构的反应,对高桩码头而言,由于子结构法的计算效率较高,建议在海工结构中使用[50-51]。当采用非线性Winkler地基上的梁模型时,其分析步骤如下:①建立不包括码头桩基和上部结构的岸坡模型,进行自由场反应分析;②用沿桩身分布的宏单元(并联弹簧和阻尼器等单元)代替土体;③建立高桩码头模型,将①得到的自由场地震动施加在宏单元末端,计算码头的地震反应[52]。如果不考虑运动作用的影响,即岸坡变形不显著的情况下,可不进行场地自由反应分析,直接将地表地震动施加在弹簧末端,并且不考虑土体阻尼的影响。
在采用直接法求解高桩码头动力反应时,一般按如下步骤进行:①建立包含岸坡和桩基及上部结构的码头模型;②确定合适的土体和结构物理和力学参数;③进行静力分析以建立码头的初始应力状态,一般考虑重力荷载及堆载的作用;④在模型底部输入地震动以进行动力分析。在确定土体和结构的材料阻尼时,一般采用Rayleigh阻尼,临界阻尼比通常取5%[53]。采用直接法时,须从半无限空间截取感兴趣的进行分析,故而模型应有足够宽度以减轻边界效应。静力分析时,一般约束侧边界的水平位移,底部采用固定边界。动力分析时,须在截取的边界上建立人工边界以模拟土体的辐射阻尼,以保证土体中产生的散射波能从有限计算区域内部穿过人工边界而不发生反射,常用的人工边界有透射边界、黏性边界、一致边界、黏弹性边界和无限元边界等[54]。一般而言,基岩处地震动通过概率地震危险性分析确定[45],也可以通过对历次地震记录的地表地震动进行反演得到模型输入界面处的地震动[55],直接将地面处记录的地震动时程施加于模型底部或将自由场地表加速度折减一半施加于基岩面是不合理的。
根据对桩的模拟方法不同,桩-土动力相互作用分析模型可分为:集中质量模型、Winkler地基上的梁模型和有限元/有限差分模型,其中Winkler地基上的梁模型在高桩码头动力分析中较为常用。Winkler地基上的梁模型通常将桩看成置于土介质中的梁,桩周土对桩的动力阻抗用连续分布的质量、弹簧和阻尼器的组合体(宏单元)代替。弹簧和阻尼器形式及连接方式多种多样,主要有Matlock模型[56],Novak模型[57],Nogami模型[58],Boulanger模型[59]和Varun模型[60]等。其中Matlock模型,Novak模型和Nogami模型较为简单、适用,但对于强震过程中桩-土界面上的分离、滑移和闭合等非线性接触现象的模拟,上述3种模型均无能为力;其他模型通过引入间隙单元、滑动元件和孔压单元等考虑这些问题,但也同时使这些模型变得非常复杂,不便于工程应用。在这些宏单元中,弹簧和与其并联的阻尼器一般是必不可少的,弹簧用于模拟土反力,一般用p-y曲线确定其刚度,阻尼器用于模拟土体的辐射阻尼。
对于梁的非线性模拟,常采用塑性铰模型和纤维模型。对于塑性铰,在分析中需要确定塑性铰恢复力模型(骨架曲线和滞回规则),骨架曲线一般通过截面的弯矩-曲率分析确定,滞回规则常用的有修正的Takeda模型[61](见图 11)。图 11中θy和θm分别为屈服转角和最大转角,My和Mm分别为屈服弯矩和最大弯矩,r为第二刚度与初始刚度之比。POLB规定,在模拟混凝土或预应力桩以及带有桩芯混凝土的钢管桩时,α和β分别取0.3和0.5;文献[62]建议对于桩顶铰,α和β分别取0.5和1,对于土内铰,α和β分别取0和0.6,因为土内铰不会受到剪切效应引起的捏缩。纤维模型是将截面按材料组成和位置进行分割,划分成一系列纤维,纤维与纤维之间服从平截面假定,通过对材料采用相应的滞回模型进而得到截面的滞回反应。其中集中塑性铰模型在SAP2000,ETABS和Perform 3D等软件中使用,纤维模型在OpenSees中使用。在ABAQUS和ANSYS等通用有限元软件中,通过选取一系列积分点,对积分点进行数值积分确定梁单元刚度,材料的非线性通过采用非线性本构关系实现。

|
图 11 修正的Takeda模型 Figure 11 Modified Takeda model |
另外,桩周土模拟中采用连续介质模型,土体简化为线弹性或黏弹性的均质或成层土;或桩周土体采用离散模型代替,离散模型通常用质量、弹簧和阻尼器等力学元件的组合体代替真实土体的作用;真实的桩周土体作为桩的约束介质,同时土体被离散为通过节点联系的有限单元/有限差分集合体[54]。
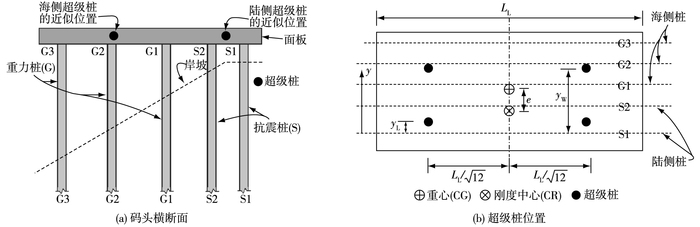
对于一般沿码头纵向规则对称的顺岸式高桩码头,上部结构在平面内外的刚度都很大,可近似为刚性,采用二维模型进行分析即可得到足够的精确度;POLB规定,对于形状不规则的码头和特殊案例(具体可见POLB),应采取三维分析方法。考虑到三维分析的计算量,POLB采用如图 12所示的“超级桩”(Super-Pile)模型,图 12针对的是一个码头分段。超级桩的位置根据图 12(a)中的重力桩(Gravity pile)和抗震桩(Seismic pile)的位置确定,重力桩主要承担竖向荷载,一般承担的地震力少于10%,抗震桩亦承担竖向地震力,但承担大部分地震力。超级桩的位置可按下式确定:
|
图 12 超级桩模型 Figure 12 Super pile model |
| ${y_{\rm{L}}} = \sum\limits_{i = S1}^{S2} {{n_i}{F_i}{y_i}} /\sum\limits_{i = S1}^{S2} {{n_i}{F_i}} ,{y_{\rm{W}}} = \sum\limits_{i = G1}^{G3} {{n_i}{F_i}{y_i}} /\sum\limits_{i = G1}^{G3} {{n_i}{F_i}} $ | (7) |
式中:yL和yW分别为陆侧超级桩和海侧超级桩距陆侧S1排桩的距离;i为桩的排数(即如图 12中S1,S2,G1,G2和G3);ni为长度LL上第i排桩的数目;Fi为推覆分析中得到的第i排桩中每根桩的水平力;yi为第i排桩距陆侧S1排桩的距离。
超级桩的刚度根据其所代表桩的Pushover曲线确定。当抗震桩达到屈服位移时,超级桩的位置基于弹性反应确定。确定重力桩刚度时,采用桩对应于相同位移时的刚度值。陆侧超级桩的刚度等于岸坡上全部陆侧桩的刚度,其余桩的刚度等于海侧超级桩的刚度。对于规则结构,两个陆侧超级桩的刚度应相同,两个海侧超级桩的刚度也应相同。为确保纵向反应下结构扭转刚度一致,超级桩应位于码头段回转中心处。对于规则码头段,超级桩至形心的距离应为
由专题I可知,非液化场地和液化场地中高桩码头的破坏形式各不相同。如果场地土为饱和砂土、粉土或混合土层等易液化土时,在抗震计算前应对土体进行液化判别。在我国港口工程中,一般参照《水运工程抗震设计规范》(JTS 146—2012)进行液化土判别;在美国,可参照文献MOTEMS,Martin和Lew[64],Youd等[65]及Boulanger和Idriss[66]。由于国内外采取的液化判别方法不同,同一种土的液化判别结果可能也不相同,李颖和贡金鑫[67]对国内外的液化判别方法进行了对比研究。
对于非液化场地上的高桩码头,一般利用Winkler地基上的梁模型进行高桩码头地震反应分析,亦有采用直接法建立桩-土-结构整体有限元/有限差分模型进行反应分析。Roth等[68]利用Perform 2D软件对美国西海岸的高桩码头进行了时程分析,并与FLAC软件的计算结果进行了对比,计算结果较为接近。另外,还利用FLAC软件建立高桩码头整体模型,土为连续介质模型,并考虑孔隙水压力的生成,结果表明土体下坡向的变形引起显著的码头侧向位移,而这一现象在采用Winkler地基上的梁模型时被忽略了。
有部分学者利用震后调查资料,研究有限元和有限差分软件进行高桩码头动力分析的合理性和有效性。Roth等[69]基于FLAC软件对美国Oakland港在1989年Loma Prieta地震中受损的3个高桩码头进行了地震反应分析,土体采用非线性模型并考虑孔隙水压力的生成,桩基采用理想弹塑性梁单元模拟,结果表明计算的反应与地震观察到的反应吻合较好,证明了FLAC软件预测码头抗震性能的有效性。Donahue[70]利用SAP2000建立的3D模型分析了奥克兰港24/25泊位在Loma Prieta地震下的反应,结果表明计算结果与记录的反应较为接近,计算的准确性依赖于所确定的表征桩-土作用的弹簧参数的合理性,码头扭转反应很小。由于地震强度不大,土体和结构的反应基本上为线性,采用开裂刚度模拟桩和理想弹塑性弹簧模拟土体并不需要考虑孔隙水压力的影响。Yan等[71]利用FLAC进行了高桩码头二维动力分析,以对中心桩的截面进行优化。
部分学者研究桩-土动力相互作用对码头地震反应的影响。丁伟农和高明[72]建立了二维高桩码头整体有限元模型考虑土体的非线性,而桩和上部结构为弹性,进行了地震反应分析。研究表明,岸坡变形对桩基内力影响较大,对烈度为8度地区,中等土质岸坡,考虑结构为弹性和土体为非线性进行计算是可行的,对8度以上地区或岸坡土体较为软弱的情况,则应同时考虑结构和土体的非线性。衣伟[73]利用Novak模型,研究了桩土动力相互作用对码头单桩地震反应的影响,分析了桩的不同破坏形式,认为当土较软时,桩顶首先破坏,当土较硬时,桩土内部首先破坏。李颖和贡金鑫[74]采用ABAQUS软件对建立的整体有限元模型进行了高桩码头地震反应分析,考虑了土体和结构的材料非线性,研究了桩基内力和塑性铰形成机制。高树飞和贡金鑫[51]利用Winkler地基梁模型研究了辐射阻尼对高桩码头非线性地震反应的影响,研究表明辐射阻尼对桩基内力和结构破坏形式有较大影响,并建议在分析中考虑辐射阻尼。
由于高桩码头的岸坡通常是倾斜的,另外有时结构布置的不对称以及堆载的不均匀,都会造成高桩码头结构的刚度中心和质量中心不对称,在纵向激励下会引起扭转反应。如专题Ⅰ所述,国外标准采用一个动力放大系数DMF对横向激励下求得的位移需求进行放大以考虑扭转效应。Benzoni和Priestley[63]利用“超级桩”模型研究了扭转效应的影响,并提出用于修正码头横向反应的计算公式。Blandon[11]通过对不同长度和宽度的高桩码头进行时程分析亦得出用于考虑码头扭转效应的经验计算式。目前,我国《水运工程抗震设计规范》(JTS 146—2012)对于扭转效应并无具体规定,国内诸多学者多是利用等效嵌固点法模拟桩-土相互作用,再将高桩码头结构予以简化并结合振型分解反应谱法进行研究。王守忠[75]将高桩码头上部结构视为一刚盘(片),并将码头下部桩基各排桩合并在一起支承面板,形成一个横向单层结构,采用振型分解反应谱法进行了平动扭转耦合分析。连竞和宋向群[76]提出按简缩后的两个自由度(平动和转动)分析高桩码头动力特性,指出规范中按单质点体系分析高桩码头动力特性的规定不尽合理。连竞和宋向群[77]根据弹性桩支承空间刚体的力学模型,分析高桩墩的动力特性,并按振型分解反应谱法给出计算水平地震惯性力和惯性扭矩的解析表达式。何良德等[78]基于基桩加刚性平台空间简化计算模型,提出了水平地震荷载作用下考虑扭转效应的全直桩码头简化计算方法。王滨等[79]利用ABAQUS软件建立的整体有限元模型研究了平面不规则码头的扭转反应,指出平面不规则使码头整体的转角增大。
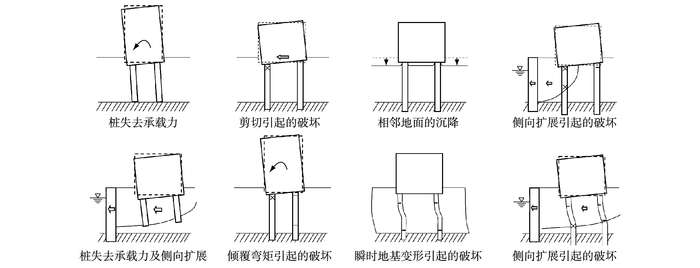
4.3 液化场地如前所述,地震中回填土和地基土的液化是造成高桩码头破坏的重要原因之一,图 13为液化引起的桩基破坏形式[80]。此图针对的是建筑物桩基,但侧向扩展引起的破坏在高桩码头中也较为常见。
|
图 13 液化土中桩基破坏形式 Figure 13 Pile foundation damage mechanisms in liquefied ground |
液化土中高桩码头的抗震分析一般采用整体有限元/有限差分模型进行,因为整体模型可以较为方便地考虑孔隙水压力的生成,而且可以一步得到分析结果,其中利用FLAC软件建立的二维非线性模型被广泛使用。如果码头性能不满足要求,则须进行土体改良,并评估改良后的性能。Yang[53]在利用现有震害案例对用FLAC建立的高桩码头二维模型校准后,研究了回填土处理和未作回填土处理的高桩码头地震反应,分析了地震引起的液化、地震动强度、桩刚度和桩“销”效应对码头抗震性能的影响,给出了考虑地震动强度、桩刚度、土密实度和不同土体处理范围的桩顶最大变形经验图表,分析采用的码头断面为美国长滩港常用的码头布置形式,考虑了16,18和24 in (1 in=25 mm)3种直径的八角形预应力混凝土桩,地震动则选取了8条震级为6~8级的地震动。Dodds等[81]利用FLAC软件评估了斐济Suva港Kings码头结构的地震稳定性,研究表明软土地基水泥土加固可有效限制深层软弱土变形。Smith等[82]利用FLAC软件对Vanterm码头进行了地震反应分析,评估了液化对码头抗震性能的影响,建议对回填土进行加固处理。Moriwaki等[83]利用FLAC软件说明了高桩码头非线性动力分析的过程,指出二维非线性动力分析是进行液化土中高桩码头动力分析的一种有效方法。由于长持时地震动更易造成码头破坏,Dickenson等[84-85]利用FLAC软件研究了长持时地震动对高桩码头的影响,结果表明采用FLAC建立的2D模型可以较好模拟地震引起的永久变形和孔隙水压力的生成,得出对于长持时地震动的分析应考虑塑性铰屈服后的软化和桩-上部结构连接的应力集中及岸坡的变形模式;并指出采用FLAC进行二维非线性分析的局限性,如不能很好地模拟桩-上部结构连接和塑性铰的滞回特性。另外,也有学者利用其他软件建立二维高桩码头模型进行动力分析。Mageau等[86]采用PLAXIS 2D软件对美国Tacoma港新建码头进行了地震反应分析,得出需要进行地基处理以减小地基变形和桩身弯矩以满足规范推荐的性能标准,另外采用碎石桩进行地基处理可有效减轻土体液化,降低土体变形和桩身剪力及弯矩。
此外,正如前文所述,在Winkler地基上的梁模型中,有很多宏单元由于引入孔压单元,可以考虑土体的液化,部分学者利用此类宏单元开展了液化土中高桩码头的动力分析。Shafieezadeh等[87]利用Varun模型在OpenSees软件中建立了高桩码头二维模型,并进行了液化土中的地震反应分析,发现强震下高桩码头遭受较大的永久变形,且受拉斜桩易发生拔出破坏,并指出液化是造成码头破坏的重要原因之一。另外,考虑到二维模型无法考虑由码头重心和刚度中心位置差异引起的扭转效应以及相邻码头段间的相互作用,Shafieezadeh等[88]又建立了高桩码头三维模型,分析中使用了一条近场地震动和一条远场地震动,分析比较了高桩码头二维地震反应和三维地震反应以及近场和远场地震动下的反应。分析表明,在地震中岸坡未遭受较大横向变形情况下,二维模型可以较为合理地估计码头的最大反应;另外,二维模型可以有效估计码头和岸坡的永久变形;近场地震动下面板位移、桩-面板连接转角和桩身曲率均较远场地震动下的大,并建议在近场地震动下采用三维模型评估码头抗震性能。
4.4 试验研究对于高桩码头的抗震性能,国内外开展了大量试验研究,主要研究结构的动力特性以及高桩码头的地震反应规律。1978年交通部第一航务工程局科学研究所对天津新港集装箱码头进行了强迫振动试验,得出码头的第一自振周期为0.31~0.33 s,第二自振周期为0.22~0.25 s,结构阻尼比为0.058~0.068[89]。高明等[90]对具有前后方平台的板梁式高桩码头、适合于大水位差的桩基多层墩式码头、桁架式高桩码头等3种码头进行了振动台试验,研究表明岸坡的影响应予以重视,将码头按单自由度体系计算与试验结果大致相近,对多层墩式码头宜按多自由度体系计算,码头叉桩的布置及其在平面上扭角的不对称性引起的码头扭转耦联振动使码头两端的动位移有相当大的增加,码头前后方平台的碰撞会加大码头的地震反应。侯瑜京等[91]对带有围堤的深水钢管桩码头开展了离心模型试验,研究了围堤和码头在施工期和使用期的变形过程,并得出了部分钢管桩受围堤及地基变形影响产生的水平位移、弯矩和土抗力的变化曲线,指出围堤在长期使用过程中仍会有较大变形。
McCullough[13]开展了高桩码头离心模型试验,并将试验结果与规范采用的设计方法(Newmark滑块位移法)以及FLAC软件的计算结果进行了对比。结果表明离心模型试验可以有效地反映码头动力反应,为验证工程实践中使用的设计方法和数值模型提供数据;岸坡永久变形是造成码头破坏的重要原因之一,在中等及以上强度的地震中应估算岸坡的永久变形;桩在地面以下一定深度的弯矩可能等于或大于桩-上部结构连接处的弯矩,特别是在软弱土和硬土的交界面处,而在采用等效嵌固点的方法中无法考虑这一现象;在考虑土体强度退化、孔隙水压力生成以及桩对岸坡稳定作用的前提下,Newmark滑块位移法的计算结果与试验结果吻合较好;与试验结果相比,使用FLAC软件建立的可考虑孔隙水压力生成的数值模型可以很好地预测变形、孔隙水压力和加速度,但桩身弯矩的预测效果较差。
Walsh和Ashford[92]为验证高桩码头桩基在达到《加州油码头抗震设计标准》[93](MOTEMS的早期版本)规定的应变限值时能否满足规定的性能标准(即可修复的非弹性变形以及防止倒塌),对长滩港的3号码头进行了现场拟静力和强迫振动试验,试验结果表明标准中采用的应变限值可行。
Takahashi和Takemura[94]针对1995 Hyogo-ken Nambu地震中受损的神户港Takahama高桩码头进行了离心模型试验,试验表明回填土和地基土的液化造成较大的护坡块石海侧运动,液化引起的桩最大弯矩的位置与震后调查的位置一致,离心模型试验可以较为合理地预测神户地震中观察到的高桩码头破坏形式;接岸结构加大了码头的海侧位移;不同液化土层厚度下地基和结构的变形模式不同,较厚的液化土层并不必然引起较大的土体和结构变形;对液化土进行处理可有效减小码头永久变形,其中对地基土的处理带来的效果好于回填土。
Chang等[95]进行了使用面波发生器的现场大尺度物理模型试验,以研究液化土中高桩码头的动力桩-土相互作用。模型由两根钢管桩和焊接在上面的钢板组成,通过震源产生的面波对桩加载,研究了剪应变-孔压生成的耦合行为、桩反应和桩-土相互作用特性。研究表明超孔压的累积受到剪应变水平的影响,且累积速率随着离桩的距离增加而减小;在使用动力p-y曲线模拟桩-土相互作用时应考虑超孔压的变化。
Boroschek等[96]进行了足尺试验研究了长375 m的高桩码头阻尼特性,研究表明码头的线性等效阻尼比约为3%,可用于运行荷载和小震下的高桩码头分析;码头上的非结构构件对码头的动力行为有较大影响,特别在纵向,建议给非结构构件提供滑动连接以将它们和码头分离或在原始设计中考虑其影响。
5 结语在考虑桩-土相互作用的高桩码头动力特性和地震反应分析方面已开展了大量理论和试验研究,取得了很多有益的结论。高桩码头动力时程分析中,关于不同计算模型(集中塑性铰模型和纤维模型)对高桩码头地震反应的影响尚未见相关报道,特别是采用集中塑性铰模型时采用何种恢复力模型应通过理论和试验研究予以明确。
目前对于近场(近断层)地震动对高桩码头抗震性能的研究较少,有关高桩码头的抗震规范中尚未考虑近断层地震动效应,应研究近断层地震动不同特性(方向性效应、滑冲效应和上盘效应等)对高桩码头抗震性能的影响。对于高桩码头体系残余变形的研究尚不够充分,已有的研究主要针对具体的码头进行分析,得出的研究成果不具有普遍适用性,仍需进一步研究和探讨。另外,尚未见有关高桩码头倒塌分析的研究,有必要开展相关研究以分析高桩码头的抗倒塌性能。对于液化场地上的高桩码头,目前有关试验研究主要集中在离心模型试验上,缺乏大比尺的振动台试验。
| [1] |
TOKIMATSU K, SUZUKI H, SATO M. Effects of inertial and kinematic interaction on seismic behavior of pile with embedded foundation[J]. Soil Dynamics and Earthquake Engineering, 2005, 25(7): 753-762. |
| [2] |
ARULMOLI A K, MARTIN G R. Seismic soil-structure interaction issues for pile-supported piers and wharves[C]// Proceedings of Conference on Lifeline Earthquake Engineering in a Multihazard Environment. 2009:930-940.
|
| [3] |
ARULMOLI A K, JOHNSON G S, YIN P, et al. Geotechnical considerations and soil-structure interaction: proposed ASCE standards for seismic design of piers and wharves[C]// Geotechnical Earthquake Engineering and Soil Dynamics Ⅳ Congress, 2008: 18-22.
|
| [4] |
Port of Long Beach. Wharf design criteria (Version 3.0)[S]. 2012.
|
| [5] |
Earth Mechanics Inc. Port-wide ground motion study, Port of Long Beach, California[R]. California: Earth Mechanics Inc, 2006.
|
| [6] |
Earth Mechanics Inc. Port-wide ground motion and Palos Verdes fault study, Port of Los Angeles, California[R]. California: Earth Mechanics Inc, 2006.
|
| [7] |
ANDERSON D G, MARTIN G R. NCHRP report 611-seismic analysis and design of retaining walls, buried structures, slopes, and embankments[R]. WASHINGTON, DC: Transportation Research Board, 2008.
|
| [8] |
AMBRASEYS N N, MENU J M. Earthquake-induced ground displacements[J]. Earthquake Engineering and Structural Dynamics, 1988, 16(7): 985-1006. DOI:10.1002/(ISSN)1096-9845 |
| [9] |
SAYGILI G, RATHJE E M. Empirical predictive models for earthquake-induced sliding displacements of slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2008, 134(6): 790-803. DOI:10.1061/(ASCE)1090-0241(2008)134:6(790) |
| [10] |
高树飞, 贡金鑫, 冯云芬. 基于规范反应谱的码头岸坡地震永久变形计算[J]. 水利水运工程学报, 2015(3): 23-31. ( GAO Shufei, GONG Jinxin, FENG Yunfeng. Estimation of earthquake-induced slope permanent deformation based on response spectrum in code[J]. Hydro-Science and Engineering, 2015(3): 23-31. (in Chinese)) |
| [11] |
BLANDON C A. Seismic analysis and design of pile supported wharves[D]. Pavia, Italy: Rose School, 2007.
|
| [12] |
BOULANGER R W, CHANG D, GULERCE U, et al. Evaluating pile pinning effects on abutments over liquefied ground[C]// Seismic Performance and Simulation of Pile Foundations in Liquefied and Laterally Spreading Ground. ASCE, 2006: 306-318.
|
| [13] |
MCCULLOUGH N J. The seismic geotechnical modeling, performance, and analysis of pile-supported wharves[D]. Oregon: Oregon State University, 2003.
|
| [14] |
MCCULLOUGH N J, DICKENSON S E, SCHLECHTER S M, et al. Centrifuge seismic modeling of pile-supported wharves[J]. Geotechnical Testing Journal, 2007, 30(5): 349. |
| [15] |
MATLOCK H. Correlations for design of laterally loaded piles in soft clay[C]// Proceeding Offshore Technology Conference, Houston, 1970:577-594.
|
| [16] |
O'NEILL M W. Group action in offshore piles[C]// WRIGHT S G. Geotechnical Practice in Offshore Engineering. New York, 1983:25-64.
|
| [17] |
American Petroleum Institute. API recommended practice 2A-WSD (RP 2A-WSD), 21st ed recommended practice for planning, designing and constructing fixed offshore platforms-working stress design[S].
|
| [18] |
JTS 167-4—2012港口工程桩基规范[S]. (JTS 167-4—2012 Code for pile foundation of harbor engineering[S]. (in Chinese))
|
| [19] |
REESE L C, COX W R, KOOP F D. Analysis of laterally loaded piles in sand[C]// Proceeding Offshore Technology Conference, Houston, 1974:473-484.
|
| [20] |
REESE L C, WELCH R C. Lateral loading of deep foundations in stiff clay[J]. Journal of Geotechnical Engineering Division, 1975, 101(7): 633-649. |
| [21] |
REESE L C, COX W R, KOOP F D. Field testing and analysis of laterally loaded piles in stiff clay[C]// Proceeding Offshore Technology Conference, Houston, 1975: 473-484.
|
| [22] |
EMI. Bi-Linear p-y curves for pier 400 piles and pendent wall[R]. California: Fugro West Inc, 1999.
|
| [23] |
KAWAMATA Y. Seismic performance of a pile-supported container wharf structures in rockfill[D]. Oregon: Oregon State University, 2009.
|
| [24] |
DIAZ G M, PATTON B W, ARMSTRONG G L, et al. Lateral load tests of piles in sloping rock fill[C]// Analysis and Design of Pile Foundations, ASCE, 1984: 214-231.
|
| [25] |
MCCULLOUGH N J, DICKENSON S E. The behavior of piles in sloping rock fill at marginal wharves[C]// Ports 2004: Port Development in the Changing World, ASCE, 2004: 1-10.
|
| [26] |
金伟良, 朱玉明, 李林普. p-y曲线法在海洋工程地基中应用的探讨[J]. 中国海上油气(工程), 1992, 4(4): 29-40. ( JIN Weiliang, ZHU Yuming, LI Linpu. Research into application of p-y curve to offshore engineering foundation[J]. China Offshore Oil and Gas (Engineering), 1992, 4(4): 29-40. (in Chinese)) |
| [27] |
GEORGIADIS M. Development of p-y curves for layered soils[C]// Proceeding of Geotechnical Practice in Offshore Engineering, ASCE, 1983: 536-545.
|
| [28] |
KAWAMATA Y, BLANDON C A, ASHFORD S A. Seismic performance of container wharf piles: test results[R]. California: University of California at San Diego, California, 2008.
|
| [29] |
ASCE/COPRI 61-14 Seismic design of piers and wharves[S].
|
| [30] |
CHEN C Y, MARTIN G R. Effect of embankment slope on lateral response of piles[C]// Proceedings of the 2nd International FLAC Conference, Lyon, France, 2001:47-54.
|
| [31] |
MEZAZIGH S, LEVACHER D. Laterally loaded piles in sand: slope effect on p-y reaction curves[J]. Canadian Geotechnical Journal, 1998, 35(3): 433-441. DOI:10.1139/t98-016 |
| [32] |
MCGANN C R, ARDUINO P, MACKENZIE-HELNWEIN P. Applicability of conventional p-y relations to the analysis of piles in laterally spreading soil[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2010, 137(6): 557-567. |
| [33] |
WILSON D W, BOULANGER R W, KUTTER B L. Seismic lateral resistance of liquefying sand[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2000, 126(10): 898-906. DOI:10.1061/(ASCE)1090-0241(2000)126:10(898) |
| [34] |
BOULANGER R W, KUTTER B L, BRANDENBERG S J, et al. Pile foundations in liquefied and laterally spreading ground during earthquakes: centrifuge experiments and analyses[R]. California: University of California at Davis, 2003.
|
| [35] |
South Carolina Department of Transportation (SCDOT). Geotechnical design manual[S]. 2010.
|
| [36] |
BRANDENBERG S J. Behavior of pile foundations in liquefied and laterally spreading ground[D].California: University of California at Davis, 2005.
|
| [37] |
Architectural Institute of Japan (AIJ). Recommendations for design of building foundations[S].2001.(in Japanese)
|
| [38] |
DOBRY R, TABOADA V, LIU L. Centrifuge modeling of liquefaction effects during earthquakes[C]// Proceeding of 1st International Conference on Earthquake Geotechnical Engineering, Tokyo, 1995:1291-1324.
|
| [39] |
DAVISON M T, ROBINSON K E. Bending and buckling of partially embedded piles[C]// Proceedings of 6th International Conference of Soil Mechanics and Foundation Engineering, Montreal, Canada, 1965:243-246.
|
| [40] |
张学言. 确定弹性桩嵌固点深度的方法[J]. 水运工程, 1980, 10: 17-21. ( ZHANG Xueyan. Method for determination of elastic pile depth to fixity[J]. Port & Waterway Engineering, 1980, 10: 17-21. (in Chinese)) |
| [41] |
CHEN Y. Assessment on pile effective lengths and their effects on design—Ⅰ. Assessment[J]. Computers & Structures, 1997, 62(2): 265-286. |
| [42] |
BUDEK A M, PRIESTLEY M J N, BENZONI G. Inelastic seismic response of bridge drilled-shaft RC pile/columns[J]. Journal of Structural Engineering, 2000, 126(4): 510-517. DOI:10.1061/(ASCE)0733-9445(2000)126:4(510) |
| [43] |
American Association of State Highway and Transportation Officials (AASHTO).LRFD bridge design specifications[S]. 3rd ed, 2004.
|
| [44] |
JTS 167-1—2010高桩码头设计与施工规范[S]. (JTS 167-1—2010 Design and construction code for open type wharf on piles[S]. (in Chinese))
|
| [45] |
Permanent International Association for Navigation Congresses (PIANC). Seismic design guidelines for port structures[S]. 2001.
|
| [46] |
UFC 4-151-10 General criteria for waterfront construction[S].
|
| [47] |
日本港湾協会. 港湾の施設の技術上の基準·同解説[S]. 2007. (Harbor Institute of Japan. Technical standards and commentaries for port and harbour facilities in Japan[S]. 2007. (in Japanese)))
|
| [48] |
桒原直範, 長尾毅. 直杭式桟橋の動的特性を考慮した照査用震度の算出方法に関する基礎的研究[R]. 日本国土交通省国土技術政策総合研究所, 2010. (NAONORI Kuwabara, TAKASHI Nagao. Fundamental study on the evaluation method of seismic coefficients of pile supported wharves considering the dynamic characteristics[R]. National Institute for Land and Infrastructure Management Ministry of Land, Infrastructure, Trasnport and Tourism, Japan, 2010. (in Japanese)))
|
| [49] |
AROTHIRAMAN R, BOOMINATHAN A. Depth of fixity of piles in clay under dynamic lateral load[J]. Geotechnical and Geological Engineering, 2013, 31(2): 447-461. DOI:10.1007/s10706-012-9597-z |
| [50] |
WERNER S D. Seismic guidelines for ports[M]. New York: ASCE, 1998.
|
| [51] |
高树飞, 贡金鑫. 基于Winkler地基梁模型的高桩码头非线性时程分析[J]. 中国港湾建设, 2015, 35(3): 14-20. ( GAO Shufei, GONG Jinxin. Nonlinear time-history analysis of pile-supported wharf based on model of beam on Winkler foundation[J]. China Harbour Engineering, 2015, 35(3): 14-20. DOI:10.7640/zggwjs201503003 (in Chinese)) |
| [52] |
SHAFIEEZADEH A. Seismic vulnerability assessment of wharf structures[D]. Georgia: Georgia Institute of Technology, 2011.
|
| [53] |
YANG Dongshan. Deformation-based seismic design models for waterfront structures[D]. Oregon: Oregon State University, 1999.
|
| [54] |
陈国兴. 岩土地震工程学[M]. 北京: 科学出版社, 2007. ( CHEN Guoxing. Geotechnical earthquake engineering[M]. Beijing: Science Press, 2007. (in Chinese))
|
| [55] |
胡少伟, 牛志国, 陆俊. 码头成层地基中地震动的非线性反演方法[J]. 水运工程, 2010(4): 7-10. ( HU Shaowei, NIU Zhiguo, LU Jun. Nonlinear inversion method of ground motion in layered soil of a quay[J]. Port & Waterway Engineering, 2010(4): 7-10. (in Chinese)) |
| [56] |
MATLOK H, FOO H C, BRAYANT L M. Simulation of lateral pile behavior under earthquake motion[C]// Specialty Conference on Earthquake Engineering and Soil Dynamics, Pasadena, 1978, (7): 600-619.
|
| [57] |
NOVAK M. Dynamic stiffness and damping of piles[J]. Canadian Geotechnical Journal, 1974, 11(4): 574-598. DOI:10.1139/t74-059 |
| [58] |
NOGAMI T, KONAGAI K. Time domain axial response of dynamically loaded single piles[J]. Journal of Engineering Mechanics, 1986, 112(11): 1241-1252. DOI:10.1061/(ASCE)0733-9399(1986)112:11(1241) |
| [59] |
BOULANGER R W, CURRAS C J, KUTTER B L, et al. Seismic soil-pile-structure interaction experiments and analyses[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1999, 125(9): 750-759. DOI:10.1061/(ASCE)1090-0241(1999)125:9(750) |
| [60] |
VARUN V, ASSIMAKI D, SHAFIEEZADEH A. Soil-pile-structure interaction simulations in liquefiable soils via dynamic macroelements: formulation and validation[J]. Journal of Soil Dynamics and Earthquake Engineering, 2013, 47(1): 92-107. |
| [61] |
TAKEDA T, SOZEN M A, NIELSEN N N. Reinforced concrete response to simulated earthquakes[J]. Journal of the Structural Division, 1970, 96(12): 2557-2573. |
| [62] |
PRIESTLEY M J N, CALVI G M, KOWALSKY M J. Displacement-based seismic design of structures[M]. IUSS Press, Pavia, Italy, 2007.
|
| [63] |
BENZONI G, PRIESTLEY M J N. Seismic response of linked marginal wharf segments[J]. Journal of Earthquake Engineering, 2003, 7(4): 513-539. |
| [64] |
MARTIN G R, LEW M. Recommended procedures for implementation of DMG special publication 117, guidelines for analyzing and mitigating liquefaction hazards in California[R]. Southern California Earthquake Center, University of Southern California, 1999.
|
| [65] |
YOUD T L, IDRISS I M, ANDRUS R D, et al. Liquefaction resistance of soils: summary report from the 1996 NCEER and 1998 NCEER/NSF workshops on evaluation of liquefaction resistance of soils[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2001, 127(10): 817-833. DOI:10.1061/(ASCE)1090-0241(2001)127:10(817) |
| [66] |
BOULANGER R W, IDRISS I M. Liquefaction susceptibility criteria for silts and clays[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(11): 1413-1426. DOI:10.1061/(ASCE)1090-0241(2006)132:11(1413) |
| [67] |
李颖, 贡金鑫. 国内外抗震规范地基土液化判别方法比较[J]. 水运工程, 2008(8): 30-38. ( LI Ying, GONG Jinxin. Comparative study on liquefaction identifying method of ground soil in seismic design code worldwide[J]. Port & Waterway Engineering, 2008(8): 30-38. (in Chinese)) |
| [68] |
ROTH W H, DAWSON E M, MEHRAIN M, et al. Analyzing the seismic performance of wharves, part 1: Structural-engineering approach[C]// Proceedings of TCLEE 2003: 6th US Conference and Workshop on Lifeline Earthquake Engineering, 2003: 385-394.
|
| [69] |
ROTH W H, DAWSON E M. Analyzing the seismic performance of wharves, part 2: SSI analysis with non-linear, effective-stress soil models[C]// Advancing Mitigation Technologies and Disaster Response for Lifeline Systems. ASCE, 2003: 395-404.
|
| [70] |
DONAHUE M J, DICKENSON S E, MILLER T H, et al. Implications of the observed seismic performance of a pile-supported wharf for numerical modeling[J]. Earthquake Spectra, 2005, 21(3): 617-634. DOI:10.1193/1.1978887 |
| [71] |
YAN L, ARULMOLI K, WEISMAIR M, et al. Seismic soil-structure interaction analyses of an underwater bulkhead and wharf system[C]// Geotechnical Engineering for Transportation Projects, ASCE, 2004: 547-555.
|
| [72] |
丁伟农, 高明. 非线性土体桩土相互作用对高桩码头抗震设计影响的分析[J]. 港工技术, 1996(4): 30-41. ( DING Weinong, GAO Ming. A study on effects of nonlinear pile-soil interaction upon seismic design of piled wharf[J]. Port Engineering Technology, 1996(4): 30-41. (in Chinese)) |
| [73] |
衣伟. 考虑桩土相互作用高桩码头单桩地震反应[J]. 港口工程, 1997(4): 30-33. ( YI Wei. Single pile seismic response for pile-supported wharf considering pile-soil interaction[J]. China Harbour Engineering, 1997(4): 30-33. (in Chinese)) |
| [74] |
李颖, 贡金鑫. 考虑桩土相互作用的高桩码头非线性地震反应分析[J]. 水利水运工程学报, 2010(2): 92-99. ( LI Ying, GONG Jinxin. Nonlinear seismic response considering soil-pile analysis of wharf structure dynamic interaction[J]. Hydro-Science and Engineering, 2010(2): 92-99. (in Chinese)) |
| [75] |
王守忠. 高桩码头平移扭转耦联振动分析与地震反应[J]. 港口工程, 1989(1): 1-12. ( WANG Shouzhong. Analysis of coupled translation and torsion vibration and seismic response of pile-supported wharves[J]. China Harbour Engineering, 1989(1): 1-12. (in Chinese)) |
| [76] |
连竞, 宋向群. 高桩码头动力特性及地震反应[J]. 港工技术, 1991(1): 7-12. ( LIAN Jing, SONG Xiangqun. Dynamic characteristics and seismic response for pile-supported wharves[J]. Port Engineering Technology, 1991(1): 7-12. (in Chinese)) |
| [77] |
连竞, 宋向群. 高桩墩的地震扭转效应[J]. 水运工程, 1994(12): 43-45. ( LIAN Jing, SONG Xiangqun. Seismic torsional effect for pile-supported pier[J]. Port & Waterway Engineering, 1994(12): 43-45. (in Chinese)) |
| [78] |
何良德, 张海荣, 杨洋, 等. 考虑扭转效应的全直桩码头动力简化计算方法[J]. 河海大学学报(自然科学版), 2013, 41(3): 265-270. ( HE Liangde, ZHANG Hairong, YANG Yang. Simplified dynamic calculation method for all-vertical-piled wharf considering torsional effect[J]. Journal of Hohai University (Natural Sciences), 2013, 41(3): 265-270. (in Chinese)) |
| [79] |
王滨, 李颖, 朱彬彬, 等. 平面形状不规则对高桩码头地震效应的影响[J]. 水电能源科学, 2014, 32(1): 84-88. ( WANG Bin, LI Ying, ZHU Binbin, et al. Seismic effect of irregular plane shape on pile-supported wharf[J]. Water Resources and Power, 2014, 32(1): 84-88. (in Chinese)) |
| [80] |
TOKIMATSU K, MIZUNO H, KAKURAI M. Building damage associated with geotechnical problems[C]// Special Issue of Soils and Foundations, Japanese Geotechnical Society, 1996:219-234.
|
| [81] |
DODDS A M, MARTIN G R, ARULMOLI K, et al. Lifeline upgrade for a wharf in soft ground[C]// Proceedings of Geo-Trans, ASCE, 2004: 1739-1746.
|
| [82] |
SMITH D, NAESGAARD E, KULLMANN H. Seismic design of a new pile and deck structure adjacent to existing caissons founded on potentially liquefiable ground in Vancouver, BC[C]// Proceedings of 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada. 2004.
|
| [83] |
MORIWAKI Y, TAN P, CHOI Y. Nonlinear analyses for design of piles in liquefying soils at port facilities[C]// Seismic Performance and Simulation of Pile Foundations in Liquefied and Laterally Spreading Ground. ASCE, 2006: 192-203.
|
| [84] |
DICKENNSON S, YANG S, SCHWARM D, et al. Use of strong motion records to validate dynamic soil-foundation-structure interaction models for pile supported wharves[C]// Proceedings of SMIP13 Seminar on Utilization of Strong-Motion Data, Los Angeles, California, 2013:47-66.
|
| [85] |
DICKENSON S, YANG S, SCHWARM, et al. Seismic performance analysis of pile-supported wharves subjected to long-duration ground motions[C]// SMIP14 Proceedings of Seminar on Utilization of Strong-Motion Data, Los Angeles, California, 2014: 63-82.
|
| [86] |
MAGEAU D W, CHIN K H. Finite element modeling of new marine terminal at the port of Tacoma[C]// Ports 2007: 30 Years of Sharing Ideas: 1977—2007. ASCE, 2007: 1-10.
|
| [87] |
SHAFIEEZADEH A, DESROCHES R, RIX G J, et al. Seismic performance of pile-supported wharf structures considering soil-structure interaction in liquefied soil[J]. Earthquake Spectra, 2012, 28(2): 729-757. DOI:10.1193/1.4000008 |
| [88] |
SHAFIEEZADEH A, DESROCHES R, RIX G J, et al. Three-dimensional wharf response to far-field and impulsive near-field ground motions in liquefiable soils[J]. Journal of Structural Engineering, 2012, 139(8): 1395-1407. |
| [89] |
交通部第一航务工程局科学研究所. 天津新港集装箱码头强迫振动试验报告[R]. 天津: 交通部第一航务工程局科学研究所, 1979. (Scientific Research Institute of CCCC First Harbor Engineering Bureau. Report on forced vibrationtests of container wharf at Tianjin New Port[R]. Tianjin: Scientific Research Institute of CCCC First Harbor Engineering Bureau, 1979. (in Chinese))
|
| [90] |
高明, 赵颖, 靳道斌. 桩基码头抗震试验研究及动力分析[J]. 水利水运科学研究, 1981(4): 37-50. ( GAO Ming, ZHAO Yin, JING Daobin. Seismic experimental studies and dynamic analysis of pile-supported piers[J]. Journal of Nanjing Hydraulic Research Institute, 1981(4): 37-50. (in Chinese)) |
| [91] |
侯瑜京, 韩连兵, 梁建辉. 深水港码头围堤和群桩结构的离心模型试验[J]. 岩土工程学报, 2004, 26(5): 594-600. ( HOU Yujing, HAN Lianbing, LIANG Jianhui. Centrifuge modeling of sea dike and pile groups in a harbour[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(5): 594-600. (in Chinese)) |
| [92] |
WSLSH S M, ASHFORD S A. Full-scale lateral load testing of pier 3 at the port of Long Beach[R]. California: University of California at San Diego, 2004.
|
| [93] |
FERRITTO J, DICKENSON S, PRIESTLEY N, et al. Seismic criteria for California marine oil terminals[R]. California: Naval Facilities Engineering Service Center, 1999.
|
| [94] |
TAKAHASHI A, TAKEMURA J. Liquefaction-induced large displacement of pile-supported wharf[J]. Soil Dynamics and Earthquake Engineering, 2005, 25(11): 811-825. DOI:10.1016/j.soildyn.2005.04.010 |
| [95] |
CHANG W J, CHEN J F, HO H C, et al. In situ dynamic model test for pile-supported wharf in liquefied sand[J]. Geotechnical Testing Journal, 2010, 33(3): 212-224. |
| [96] |
BOROSCHEK R L, BAESLER H, VEGA C. Experimental evaluation of the dynamic properties of a wharf structure[J]. Engineering Structures, 2011, 33(2): 344-356. DOI:10.1016/j.engstruct.2010.10.014 |
2. School of Architecture and Civil Engineering, Liaocheng University, Liaocheng 252059, China
 2017
2017 