滑坡与地震、火山喷发并列为三大地质灾害,引起滑坡的原因主要是强降雨和地震。因此,相当一部分滑坡可以看成是地震的次生灾害。2008年四川汶川8.0级地震引起地质灾害5 430处,其中滑坡3 572处,崩塌为600处,泥石流为737处,不稳定斜坡为521处,均与边坡在地震作用下的失稳破坏有关。边坡的地震动力分析是岩土工程界和地震工程界的研究热点。近年来,很多专家学者对于地震作用下边坡动力响应的数值模拟进行了大量研究。何蕴龙等[1]通过有限元动力分析方法,得到了岩石边坡地震作用近似计算方法;祁升文等[2-3]通过大量数值模拟,发现了高、低边坡动力反应的不同形式;言志信等[4-5]对于顺层岩质边坡地震作用下的加速度响应规律、频谱特性、破裂面位置以及失稳的判定进行了较全面的研究,并对耦合地震波作用、多级平台和黄土地质等情况进行了研究;徐光兴等[6]对边坡地震动力响应做了大量的模型试验,所得结果与模拟计算结果大致吻合。但无论是数值模拟还是物理模型试验,均未考虑地下水的作用。
实际上,边坡岩土体是由岩石(或土)、水、气构成的三相体系,大多数岩土体的动力反应均有地下水的参与。因此,地震作用下岩土体的动力反应是一个极其复杂的流固耦合过程,流体赋存于岩土体的孔隙中,会使岩土体的质量增加,改变质量分布,从而使其模态发生改变;同时也会使岩土体的应力状态产生变化,根据有效应力原理,总应力由岩土体骨架所受的有效应力和孔隙水压力共同承担。在不透水条件下,孔隙水压力不断累积,岩土体的动力指标,如位移、速度、加速度、动应力、动应变等均受到孔隙中所含水分的制约与影响[3],流固二相体系的动力特性必将有所改变,而且可能与单相体系差异极大。例如,自然界中水的单相体系不能传播剪切波,而赋含地下水的岩土体二相体系则恰恰相反。剪切波(地震切向力)与压缩波(地震竖向力)同样是造成边坡失稳破坏的主要原因[7],在距离震中较远的情况下,剪切波对边坡的破坏作用大于压缩波。因此,对流固二相体系的动力反应进行专门的研究非常必要。目前对地下水的研究主要集中于静力作用下,地下水位迅速上涨或下跌使边坡前缘滑动或产生超孔隙水压力对边坡稳定造成不利影响,而对于地下水位不变情况下的边坡地震动力响应研究较少。
FLAC3D适用于非线性大变形分析,在岩土领域应用非常广泛,可以模拟多孔介质中的流体流动,具有强大的渗流计算功能,并可以将渗流模型与固体(力学)模型进行耦合[8]。目前,关于赋含地下水的流固二相边坡地震动力响应的研究鲜见报道。本文就这一问题利用FLAC3D数值分析软件作了初步研究和探索。
1 模型建立 1.1 边坡模型郑颖人等[9]对于边坡模型的几何边界范围提出了具体要求:坡脚到边坡低侧边界的距离为坡高的1.5倍,坡顶到边坡高侧边界的距离为坡高的2.5倍,上下边界总高不低于2倍坡高。本模型参照这一标准并适当扩展,取坡高25 m,边坡水平距离15 m,上下边界总高55 m,坡度约为59.0°,高侧边界距离坡顶65 m,低侧边界距离坡脚50 m,顺层倾角约为49.5°。顺层岩质边坡分为两层,上层为风化表层,下层为基岩,无软弱夹层。模型中材料类型均设为弹塑性材料,采用Mohr-Coulomb屈服准则。顺层岩质边坡计算模型及岩体物理力学参数分别见图 1及表 1。

|
图 1 顺层岩质边坡几何示意(单位:m) Figure 1 Bedding rock slope geometry figure (unit: m) |
| 表 1 边坡及地下水物理力学参数 Table 1 Physico-mechanical parameters of slope and groundwater |
当地震波传播至两种介质的分界面时,会产生反射和折射,人为截断边界条件将导致地震波产生与实际情况不符的反射,可能使动力分析严重失真。因此,采用FLAC3D数值模拟软件,对边坡模型四周边界设置了自由场边界条件。通过在边界网格上设置水平和垂直阻尼器来达到自由场与主体网格的耦合,模拟了无限场地的效果,即满足吸收能量和在边界面不发生反射两个要求。对于侧面及底部基岩,所选取的阻尼具有相同形式:C=ρCpS。其中,C为广义阻尼系数;ρ为材料密度;Cp为纵波波速;S为横截面积[10]。其刚度设置没有特别要求,与对应主体网格相同即可。边界条件设置如图 2所示。实际算例表明,该边界条件对于入射角大于30°的剪切及压缩波具有较理想的吸收效果[10]。

|
图 2 地震作用下边坡边界条件示意 Figure 2 Boundary condition of slope under seismic action |
模型中地下水的水面概化为水平面,地下水面高程分别设置在40和55 m处。不考虑毛细现象,假设水面以下的岩体处于饱和状态,水面以上的岩体不含水分。模型中基岩和表面风化层的渗透系数分别取为1×10-4和1×10-2 m/s,孔隙率均取为0.25,设置地下水的体积模量为2×10-8 Pa,密度取1 000 kg/m3,其他相关参数设置见表 1。未设置比奥系数和比奥模量,不考虑岩体的可压缩性。对于流体边界条件,FLAC3D提供了透水边界和不透水边界两种模式。由于地震持续时间仅为20 s,远远小于岩体渗流作用的时间,所以采用不透水边界,即边界上节点与外界没有流体交换,边界节点上的孔压值可以自由变化。
边坡表面风化层参数根据有关规范按照Ⅲ类场地进行取值,下覆基岩考虑为砂岩或砾岩,并按其常用物理力学指标进行取值。为了在数值算例中更明显地对表面风化层和下覆基岩进行区别,边坡基岩的黏聚力和内摩擦角在正常范围内取值稍高,分别为15 MPa和54.5°。
FLAC3D提供了局部阻尼、瑞利阻尼、滞后阻尼3种阻尼形式供用户选择,模型阻尼选取为局部阻尼,阻尼系数为0.157。局部阻尼的主体思路是通过增加或减少节点质量,达到衰减能量的目的,即在速度绝对值达到最大时,节点质量减小1个定值;当速度为零时,振子质量增加1个定值。因此,每循环1个振动周期都会产生1个能量耗散,1个周期内能量的损耗与最大存储能量的比值为比损耗(由临界阻尼比求得),局部阻尼系数即由比损耗确定。
1.3 动孔压模型近40年来,国内外许多学者对振动孔隙水压力的理论与应用开展了深入而广泛的研究,先后提出了数十种孔压计算模型。FLAC3D中内置的Finn模型属于应变模型,其实质是在Mohr-Coulomb模型的基础上增加了动孔压的上升模式,假定动孔压的上升与塑性体积应变增量有如下关系:
| $\Delta u = {\overline E _{\rm{r}}}\Delta {\varepsilon _{{\rm{vd}}}}$ | (1) |
式中:Δu为不排水条件下孔隙水压力的增量;
根据G. R. Martin等[11]的研究,认为塑性体积应变与循环剪应变幅值之间的关系与固结压力无关,塑性体积应变增量仅是总的累积体积应变和剪应变的函数:
| $\Delta {\varepsilon _{{\rm{vd}}}} = {C_1}(\gamma - {C_2}{\varepsilon _{{\rm{vd}}}}) + \frac{{{C_3}\varepsilon _{{\rm{vd}}}^2}}{{\gamma + {C_4}{\varepsilon _{{\rm{vd}}}}}}$ | (2) |
式中:εvd为累积永久塑性体积应变;γ为循环剪应变幅值;C1,C2,C3,C4为模型常数。参考FLAC3D手册,各系数取值如下:C1=0.8,C2=0.79,C3=0.45,C4=0.73。
需要说明的是,流固耦合的计算机制主要是根据试验总结出的动孔压模型,求出每一时间步的应变增量,回代入结构动力方程,对该时间步的固相应变进行修正,利用修正后的值进行下一步固相动力响应计算,同时继续利用动孔压模型修正固相应变,循环往复,最终得到流固耦合系统的动力响应[10-11]。
2 含地下水边坡的加速度响应规律 2.1 地震波输入选择实测天津波南北向动力时程(持续时间共19.19 s,峰值加速度为1.458 m/s2,相当于7度基本烈度[12])经滤波和基线调整后,作为地震动输入,加速度时程曲线如图 3所示。边坡的动力响应包括加速度、速度、位移、动应力和动应变响应等,其加速度响应及其分布规律是评价边坡地震动力响应的基本资料,动力作用下边坡可能发生的残余变形也是工程最关心的问题。因此,主要研究了顺层边坡的加速度响应规律,并对变形规律作了初步分析。

|
图 3 地震波加速度时程曲线 Figure 3 Seismic wave acceleration curve |
图 4是图 1中A,B两点经平滑处理后的超孔隙水压力变化时程,可以看出A,B点的超孔隙水压力没有随加速度衰减而立即开始消散,而是在短期内继续上升,与文献[13]中观察到的现象相符,可能是因为边坡在纵横向耦合地震波的作用下处于非线性变形状态,当输入振动减弱时,变形仍然保持较大的规模并持续发展,使超孔隙水压力表现为持续上升。图中B点距离边坡临空面较近,渗流路径较短,因而超孔隙水压力消散快于A点。

|
图 4 监测点超孔隙水压力变化时程 Figure 4 Change process of excess pore water pressure at monitoring points |
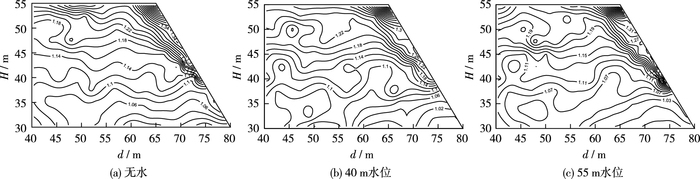
沿边坡厚度方向距离原点(O点)11 m且垂直于边坡厚度方向的平面将坡体切开,以该平面代替整个坡体作加速度响应规律分析。定义坡体上某点加速度响应时程峰值(PGA)和坡脚点(O点)加速度响应时程峰值之比为PGA的放大系数,坡面一定范围内无水、水位40和55 m时的PGA放大系数等值线图见图 5。从图 5(a)中可见,不考虑地下水的情况下,坡面附近加速度分布规律呈现明显的垂直放大效应和临空面放大效应,与其他学者[14]的结论相符,其中坡顶点的PGA放大系数最大,达到1.60。从等值线分布规律来看,基本符合低边坡动力反应类型。图 5(b)是水位40 m时的PGA放大系数等值线图,坡面垂直放大效应和临空面放大效应仍然存在,但相对于无水坡体的情况,更具有规律性,总体上满足垂直放大效应和临空面放大效应,但局部区域存在多处明显的“环状”等值线,表明该位置处的PGA放大系数产生异常,该点加速度峰值明显高于或低于周围节点的加速度峰值,与总体趋势相悖。同时,数值分析结果表明40 m水位PGA放大系数在坡顶达到最大值,为1.64,略大于无水情况。图 5(c)是水位55 m时的PGA放大系数等值线图,此时整个边坡处于饱和状态,其节律性相对于无水坡体同样很明显,总体上仍然符合垂直放大效应和临空面放大效应的规律。坡顶处PGA放大系数最大,达到1.69,大于无水及40 m水位的情况。由此,可以总结出一般性的规律:含水边坡坡顶的加速度响应峰值和PGA放大系数大于不含水边坡;顺层岩体内赋存的水分会对PGA放大系数的分布产生扰动,对PGA放大系数等值线图产生节律性的影响,可能是由于地震波在岩土和水两种介质中传播将产生大量反射、干涉等现象而造成,但加速度垂直放大和临空面放大的总体趋势不会发生改变。
|
图 5 不同水位下的PGA放大系数等值线 Figure 5 Contour map of PGA amplification factor under different water levels |
为了进一步分析水位对顺层岩质边坡加速度动力响应的影响规律,分别对35,45和50 m水位时边坡的加速度响应作了分析,得到如下结果。图 6和图 7包含了不同水位下边坡坡脚加速度响应峰值、坡顶加速度响应峰值和PGA放大系数的变化趋势。

|
图 6 不同水位下坡顶、坡脚加速度峰值 Figure 6 Peak acceleration at top and toe of slope under different water levels |

|
图 7 坡顶监测点PGA放大系数 Figure 7 PGA amplification factor at top of slope |
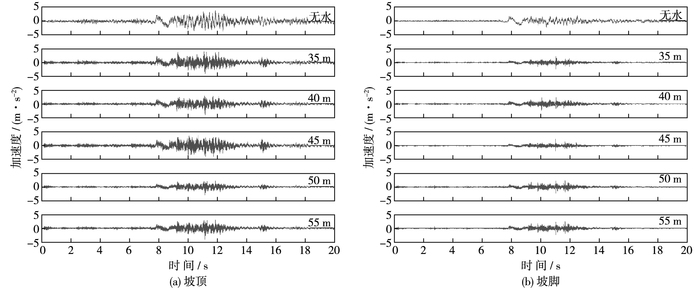
为了进一步分析地下水对边坡加速度分布的影响,图 8给出了不同水位下,坡顶和坡脚加速度时程曲线。可见,相对于不考虑地下水的情况,含地下水时加速度时程改变较为明显。而对于考虑不同水位的情况,加速度时程大致趋势保持一致,局部波动有所改变,可能是因为不同水位的地下水对边坡系统质量,刚度的影响存在差异,从而使得边坡自振特性存在差异,以及不同水位地下水的反射、干涉等条件不同而导致。
|
图 8 不同水位下坡顶和坡脚加速度时程对比 Figure 8 Comparison between acceleration histories of top and toe of slope under different water levels |
根据以上综合分析可知,含水边坡的PGA放大系数均略大于无水边坡,但仅就含水边坡自身变化而言,PGA放大系数随水位上升呈波动状态,总体上升趋势并不明显。从加速度变化角度来看,水位35,40,45和50 m情况下的坡脚加速度峰值相对无水时坡脚加速度峰值的变化趋势不明显,但饱和状态下(即水位55 m时),坡脚加速度峰值呈现“跳跃式”增长,这一现象同样存在于坡顶最大加速度峰值的变化之中。对于坡顶加速度峰值,赋含地下水边坡相对于无水边坡的坡顶加速度呈现明显的增大趋势,但含水边坡自身不同水位情况下加速度的变化却呈现波动状态,上升趋势不明显,饱和状态下的坡顶加速度峰值同样呈现“跳跃式”变化。就PGA放大系数等值线而言,含水边坡的分布更为“杂乱”,规律性较差,可能是由于地震波在孔隙水与岩土体骨架两种介质之间传播导致反射、折射等现象频繁发生的原因。由于地下水对系统自振特性的影响以及不同水位地下水的反射和干涉条件不同,导致考虑与不考虑地下水时加速度响应显著改变,考虑不同水位时加速度时程趋势一致但局部波动存在明显差异。
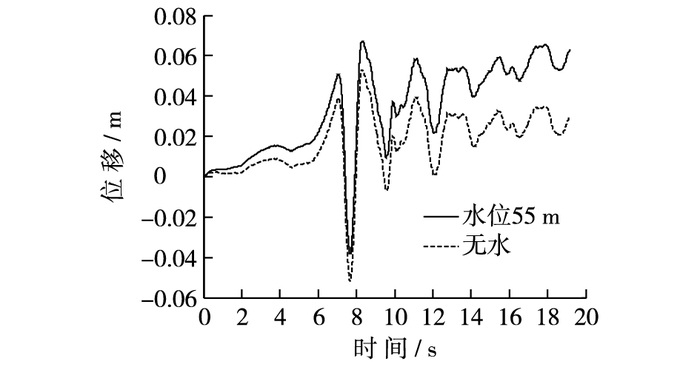
3 地下水对边坡稳定性的影响 3.1 地下水位对坡面位移的影响图 9为无水和水位55 m情况下坡顶监测点x向位移的变化情况。相对于无水边坡,赋含地下水边坡的坡顶最大位移明显增大。无水时,坡顶x方向最大位移为5.3 cm,考虑地下水时,坡顶位移最大可达7.1 cm,较无水情况增大了34%。由此可知,地下水对于坡顶位移有明显的放大作用,地下水的存在对于边坡地震稳定性不利。图 10给出了不同地下水位情况下地震结束时坡面各点的残留位移。可见,无水情况下坡面各点的残留位移显著小于考虑地下水的情况,而随着水位以及坡面各点位置的升高,残留位移逐渐增大。
|
图 9 两种情况下坡顶x向最大位移时程曲线 Figure 9 Time history curves of maximum displacement on top of slope in x direction |

|
图 10 地震结束时坡面各点残留位移 Figure 10 Residual displacement of slope at end of earthquake |
从图 11可见,塑性区集中在表面风化层,无水情况下多数单元主要受剪切破坏,少量单元为拉剪共同作用破坏。随着地下水位的升高,拉剪共同作用破坏单元逐渐增加,这表明对顺层岩质边坡的破坏效应逐渐增加。从图 11还可看出,由于水位升高而增加的拉剪共同作用破坏单元有一部分位于滑坡体上缘,说明地下水位的升高将促使滑动体上缘的张拉破坏。

|
图 11 不同水位下的塑性区分布 Figure 11 Distribution of plastic zone under different water levels |
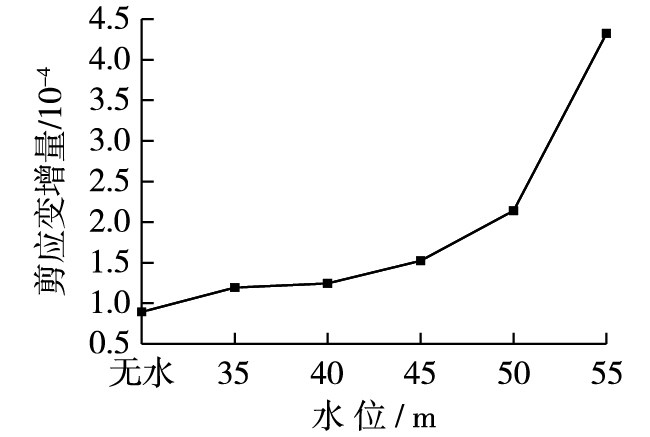
图 12给出了不同水位下塑性区最大剪应变增量的变化情况,可见随着水位的升高,塑性区最大剪应变增量逐渐增大。从塑性破坏区分布和剪应变增量情况来看,地下水对顺层岩质边坡的稳定是不利的。
|
图 12 不同水位下的塑性区最大剪应变增量 Figure 12 Max shear strain increments of plastic zone under different water levels |
根据动力数值模拟分析,赋含地下水的顺层岩质边坡的加速度响应规律与无水的顺层岩质边坡相比既有相似也有差异。相似部分在于垂直放大效应与临空面放大效应较为明显;差异部分在于考虑地下水时,坡顶、坡脚加速度和PGA放大系数都有不同程度的增大,且当边坡处于整体饱和状态时,坡顶、坡脚加速度明显增大。含水边坡的PGA放大系数等值线图比不含水边坡更为“杂乱”,可能是由于地震波在孔隙水与岩土体骨架两种介质之间传播导致反射、折射等现象频繁发生的原因。
有水情况下的坡顶位移比无水时显著增大。塑性区主要分布于表面风化层,不考虑地下水时以剪切破坏为主,少量单元呈拉剪共同作用破坏状态;考虑地下水时,拉剪共同作用单元随水位的升高而增加,表明边坡的破坏效应逐渐增大;并且滑坡体上缘的拉剪共同作用破坏单元逐渐增加,表明地下水位的升高将促进滑坡体上缘的张拉破坏。因此,地下水的存在对于顺层岩质边坡地震作用下的稳定不利。
在现有条件下,数值分析模型只能是一个经过多重简化的概化模型,在很多方面还有待进一步改进,尤其是动力作用下的流固耦合作为一个极其复杂的力学过程,在模拟岩土体不完全饱和状态,确定滑坡体内部浸润面,以及直接求解流固耦合动力方程等方面仍需改进。
| [1] |
何蕴龙, 陆述远. 岩石边坡地震作用近似计算方法[J]. 岩土工程学报, 1998, 20(2): 66-68. ( HE Yunlong, LU Shuyuan. A method for calculating the seismic action in rock slope[J]. Chinese Journal of Geotechnical Engineering, 1998, 20(2): 66-68. (in Chinese)) |
| [2] |
祁生文. 单面边坡的两种动力反应形式及其临界高度[J]. 地球物理学报, 2006, 49(2): 518-523. ( QI Shengwen. Two patterns of dynamic responses of single-free-surface slopes and their threshold height[J]. Chinese Journal of Geophysics, 2006, 49(2): 518-523. (in Chinese)) |
| [3] |
祁生文, 伍法权, 刘春玲, 等. 地震边坡稳定性的工程地质分析[J]. 岩石力学与工程学报, 2004, 23(16): 2792-2797. ( QI Shengwen, WU Faquan, LIU Chunling, et al. Engineering geology analysis of stability of slope under earthquake[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(16): 2792-2797. DOI:10.3321/j.issn:1000-6915.2004.16.024 (in Chinese)) |
| [4] |
言志信, 张刘平, 曹小红, 等. 地震作用下顺层岩质边坡动力响应规律及变形机制研究[J]. 岩土工程学报, 2011, 33(增1): 54-58. ( YAN Zhixin, ZHANG Liuping, CAO Xiaohong, et al. Dynamic response and deformation mechanism of a bedding rock slope under earthquakes[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(Suppl1): 54-58. (in Chinese)) |
| [5] |
言志信, 高乐, 彭宁波, 等. 顺层岩质边坡地震动力响应研究[J]. 岩土力学, 2012, 33(增2): 85-90. ( YAN Zhixin, GAO Le, PENG Ningbo, et al. A study of dynamic response of bedding rock slope under earthquakes[J]. Rock and Soil Mechanics, 2012, 33(Suppl2): 85-90. (in Chinese)) |
| [6] |
徐光兴. 地震作用下边坡工程动力响应与永久位移分析[D]. 成都: 西南交通大学, 2010. (XU Guangxing. Research on the dynamic responses and permanent displacement of slope under earthquake[D]. Chengdu: Southwest Jiaotong University, 2010. (in Chinese))
|
| [7] |
许强, 黄润秋. 5.12汶川大地震诱发大型崩滑灾害动力特征初探[J]. 工程地质学报, 2008, 16(6): 721-729. ( XU Qiang, HUANG Runqiu. Kinetics characteristics of large landslides triggered by May 12th Wenchuan earthquake[J]. Journal of Engineering Geology, 2008, 16(6): 721-729. (in Chinese)) |
| [8] |
ITASCA Consulting Group. FLAC3D Version 4.0 (fast lagrangian analysis of continua in 3 dimensions) user's manual[M]. USA: Itasca Consulting Group, 2009.
|
| [9] |
郑颖人, 赵尚毅, 张鲁渝. 用有限元强度折减法进行边坡稳定分析[J]. 中国工程科学, 2002, 4(10): 57-62. ( ZHENG Yingren, ZHAO Shangyi, ZHANG Luyu. Slope stability analysis by strength reduction FEM[J]. Engineering Science, 2002, 4(10): 57-62. DOI:10.3969/j.issn.1009-1742.2002.10.011 (in Chinese)) |
| [10] |
陈育民, 徐鼎平. FLAC/ FLAC3D基础与工程实例[M]. 2版. 北京: 中国水利水电出版社, 2013. ( CHEN Yumin, XU Dingping. Basic theory and engineering examples of FLAC/ FLAC3D[M]. 2nd ed. Beijing: China Water and Power Press, 2013. (in Chinese))
|
| [11] |
MARTIN G R, FINN W D L, SEED H B. Fundamentals of liquefaction under cyclic loading[J]. Journal of the Geotechnical Engineering Division, ASCE, 1982, 108(7): 835-952. |
| [12] |
胡聿贤. 地震工程学[M]. 北京: 地震出版社, 1988. ( HU Yuxian. Seismic engineering[M]. Beijing: Earthquake Press, 1988. (in Chinese))
|
| [13] |
吕西林, 任红梅, 李培振, 等. 液化场地自由场体系的数值分析及振动台试验验证[J]. 岩石力学与工程学报, 2009, 28(增2): 4046-4053. ( LYU Xilin, REN Hongmei, LI Peizhen, et al. Numerical analysis of free field system in liquefiable site and validation of shaking table tests[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(Suppl2): 4046-4053. (in Chinese)) |
| [14] |
王存玉. 地震条件下二滩水库岸坡稳定性研究[M]//岩体工程地质力学问题(七). 北京: 科学出版社, 1987. (WANG Cunyu. Study on the slope stability of Ertan reservoir under seismic excitation[M]// Geomechanics problems in rock engineerings (Ⅶ). Beijing: Science Press, 1987. (in Chinese))
|
 2017
2017 
