水电工程高边坡是一个巨大、复杂、开放及动态的系统,受到系统内在因子和外在因子的共同影响,其整体稳定性评价一直是高边坡工程研究的一个难点和热点问题[1-4]。对边坡整体稳定性进行评价,虽然评价方法多种多样,但常用的方法是通过选取影响边坡稳定的多种因子,构建边坡稳定评价的多层次多指标体系,运用定性或定量化的评价方法,对边坡稳定状态做出模糊性综合评价。目前国内外学者针对边坡稳定性问题开展了大量研究并取得了一定的成果。如秦植海等[5]通过构建岩质高边坡稳定性评价的指标体系及其评价等级标准,建立了高边坡稳定性评价的模糊层次与集对分析(FAHP-SPA)耦合模型,据此评价了三峡永久船闸岩质高边坡的稳定性。徐飞等[6]建立了边坡稳定性评价的粒子群优化投影寻踪模型(PSO-PP),并将该模型应用于雅砻江锦屏一级水电站左岸边坡的稳定性评价中。罗勇[7]对岩质边坡的稳定性影响因素进行了详细分析,对岩质边坡的破坏模式进行了分析研究,对岩质边坡进行结构分类、采用不同指标对边坡破坏模式进行分析,建立岩质边坡稳定性评价体系,并指出了边坡稳定性分析中多种方法及其优缺点。何海鹰等[8]基于层次分析法构建了适于高速公路边坡养护管理的岩质高边坡风险评估指标体系。王新民等[9]运用可拓学理论构造经典域物元、节域物元和可拓集合中的关联函数,研究了岩质边坡稳定性安全评价的层次分析法-可拓学模型在高边坡稳定性评价中的应用。Liu等[10]基于云模型对山区水电站岩质边坡稳定性进行综合评价。Su等[11]基于模糊集优化认知理论和实例推理系统对水电站岩质边坡进行稳定性分析。舒苏荀等[12]采用神经网络改进模糊点估计法计算了边坡稳定可靠度指标。
尽管目前有关高边坡稳定性评价研究取得了可喜进展,但是大多研究只注重位移速率、破坏模式识别和边坡灾害分区等单效应的一维评价。边坡稳定性的影响因素很多,但评估指标的不确定性对边坡稳定性评价影响的研究还较少。其次,目前采用的边坡安全评价方法未能融合复杂岩体应力、边坡特征、岩石性质、岩体结构、自然因素与人类活动等因素及其权重的影响,故难以客观综合评价边坡整体稳定性。
针对上述高边坡稳定性评价中指标赋权及其模糊隶属度等不确定问题,本文提出了一种基于组合赋权模糊云理论的高边坡稳定性评价方法。该方法通过构建多因素协同系统效应的高边坡稳定性评价指标体系及其等级划分标准,综合利用梯层指标的主客观组合赋权方法,结合其评价中模糊性与随机性特点,引入模糊熵和云理论,建立了适用于高边坡稳定性多维梯级评价云模型。最后,利用该方法对锦屏Ⅰ级水电站左岸边坡进行稳定性评价,据此验证本文提出方法的科学性和有效性。
1 高边坡稳定性评价指标体系的构建及指标赋权 1.1 评价指标体系的构建边坡稳定性的影响因素众多,根据待评边坡特性,选用全面合理的评价指标,构建边坡稳定性评价指标体系,是进行边坡稳定性综合评价的关键。借鉴同领域其他学者[13-15]对边坡安全稳定性评价指标给定的分类标准,类比分析国内的部分水利水电岩石高边坡工程,将评价指标分为地质因素(X1)、工程因素(X2)、环境因素(X3)和监测因素(X4)四大类,以此作为一级评价指标,选取X11~X16,X21~X24,X31~X34和X41~X44共18个评价因子作为二级评价指标,参照《水利水电工程边坡设计规范》将边坡整体安全等级分为5个等级:Ⅰ级极不稳定、Ⅱ级不稳定、Ⅲ级基本稳定、Ⅳ级稳定、Ⅴ级极稳定,详见表 1。
| 表 1 评价指标体系及其等级标准 Table 1 Evaluation index system and its standards |
权重是对指标在评价体系中相对重要程度的描述。目前,确定权重的方法有很多种,为克服主观权重的不足和弥补客观权重的缺陷,在规避权重主观性的同时,为保证权重的相对客观科学性,采用熵组合权重法确定各项评价指标的权重系数。
对各项评价指标所涉及的各类专家进行正式咨询调查,整理汇总得到各项评价指标的主观权重W1(i),其中i = 1,2,…,n,n为指标个数。采用熵权法[16]计算综合评价中各项评价指标的客观权重W2(i)。熵权法通过建立评价矩阵确定各项评价指标在综合评价过程中的权重。综合各项评价指标的主观权重W1(i)和客观权重W2(i)便可得到相应指标的组合权重W(i),显然W1(i)和W2(i)都应尽可能接近。根据最小相对信息熵原理[17],并利用拉格朗日乘子法进行优化,采用下式得到组合权重W(i):
| $W(i) = {\left[ {{W_1}(i){W_2}(i)} \right]^{0.5}}/\sum\limits_{i = 1}^n {{{\left[ {{W_1}(i){W_2}(i)} \right]}^{0.5}}} $ | (1) |
设U是一个用精确数值表示的论域,x∈U,C是论域U上的一个定性概念,任意定量值x在定性概念C上都有且只有一个对应的隶属度μC(x),且μC(x)∈0,1,μC(x)是一个具有稳定倾向的随机数。隶属度μC(x)在论域U上的分布称为云[18-19]。
| ${\mu _C}(x) \in \left[ {0,1} \right] \;\;\; \forall x \in U,x \to {\mu _C}(x)$ | (2) |
期望Ex,熵En和超熵He是云的3个基本数字特征。通常各评价指标等级标准数量级不同,因此,在计算云模型数字特征之前应当按照下式将各评价指标等级标准归一化处理[20]:
| ${p_{ij}} = \left\{ {\begin{array}{*{20}{l}} {\frac{{{x_{ij}} - {x_{j{\rm{min}}}}}}{{{x_{j{\rm{max}}}} - {x_{j{\rm{min}}}}}}({\rm{效益型指标,即指标值越大越有利的指标}})}\\ {\frac{{{x_{j{\rm{max}}}} - {x_{ij}}}}{{{x_{j{\rm{max}}}} - {x_{j{\rm{min}}}}}}({\rm{成本型指标,即指标值越小越有利的指标}})} \end{array}} \right.$ | (3) |
式中:pij为归一化指标数据。归一化处理有效地消除了指标间的不可公度。归一化结果可表示为{C1,C2,…,Cn}=[0,a1],(a1,a2],…, (an-1,1]。若指标等级标准具有双边界限,如x∈(a,b),则其云模型参数计算式如下:
| $\left\{ {\begin{array}{*{20}{l}} {{E_x} = (a + b)/2}\\ {{E_{\rm{n}}} = (b - a)/6}\\ {{H_{\rm{e}}} = k} \end{array}} \right.$ | (4) |
式中:k为常数,可以根据评语集的模糊熵进行调整。若指标等级标准只有单边界限,如
正向云发生器[21]:若x满足
| ${\mu _C}(x) = \exp \left[ { - {{(x - {E_x})}^2}/2{{(E_{\rm{n}}^′)}^2}} \right]$ | (5) |
X-条件云发生器:当x已知,结合云数字特征,运用式(5) 进行计算即可得云滴drop(x,μ)。在用X-条件云发生器计算隶属度之前,需对实测数据值进行归一化。
2.2 融入模糊熵的边坡稳定性二维评价云模型在信息论中,熵用以度量事件的不确定性。将熵推广到模糊集上称为模糊熵[22],是一种描述模糊集的模糊性程度的数学工具,用符号E表示。边坡稳定性评价是多层次多指标的综合评价,信息量大,各项评价指标等级归属差异也很大,通常仅以单一的等级评价做出定性结论难以真实全面地反映边坡稳定性状态,因此在边坡稳定性评价中引入模糊熵E,对云模型的综合评价结果进行复杂度分析,作为等级评价的辅助参评量,并得到最终的二维评价结果(L,E),模糊熵E的计算如下:
| $E = m\sum\limits_{i = 1}^n {\left[ {\mu \ln {\mu _i} + (1 - {\mu _i})\ln (1 - {\mu _i})} \right]} $ | (6) |
| $m = - \frac{1}{{\ln \left[ {{{(n - 1)}^{1 - n}}{n^n}} \right]}}$ | (7) |
式中:n为总等级数,i = 1,2,…,n;μi为边坡稳定性对应等级i的隶属度;m为标准化系数,由式(6) 和(7) 计算即可得到综合隶属度向量的复杂度。依据上述模糊熵公理,现将等级综合评价结果的复杂度与模糊熵E的对应关系规定为:[0,0.2],(0.2,0.4),[0.4,0.6],(0.6,0.8),[0.8,1.0]分别对应明显、较明显、模糊、较明显、明显。当计算结果为明显或较明显时,说明各项评价指标等级归属差别较小,边坡稳定性等级综合评价结果复杂程度低;相反,当计算结果为模糊时,说明各项评价指标等级归属差别较大,边坡稳定性等级综合评价结果复杂程度高。
根据上述构建边坡稳定性评价方法,依托MATLAB程序平台,建立融入模糊熵的边坡稳定性二维评价云模型,具体实施步骤为:
(1) 根据边坡特点选取边坡稳定性评价指标,参考专家意见,将指标分层归类,并按照相关规范拟定分级标准,构建边坡稳定性评价指标体系;
(2) 对专家走访或其他方式进行正式调查确定主观权重W1,结合评价指标体系,运用熵权法确定客观权重,采用熵组合权重法确定各项评价指标的组合权重W;
(3) 基于云模型理论,依据各项评价指标的分级标准计算各对应等级的云模型参数,运用正向云发生器生成各项评价指标的隶属云;
(4) 将待评价边坡的实测数据代入X-条件云发生器,求解得到各项评价指标对应各等级隶属度μ,结合Step2中所得组合权重W,由式(8) 计算得到等级综合评价隶属度向量,最后依据最大隶属度原则确定边坡稳定性等级L;
| $R = \sum\limits_{i = 1}^n {{\mu _i}{W_i}} $ | (8) |
(5) 依据模糊熵理论,由式(6) 和(7) 计算出边坡稳定性等级综合评价的模糊熵E,分析等级综合评价结果的复杂程度,从而得到边坡稳定性二维评价结果(L,E)。
3 工程实例锦屏Ⅰ级水电站位于盐源县和木里县境内的雅砻江干流,坝顶高程1 885 m,坝高305 m,其左岸坝肩高陡边坡为反向坡,是目前水利水电工程中最陡的边坡开挖工程之一。左岸拱肩部位坡度较陡,绝大部分基岩裸露,1 850 m高程以下为大理岩,中低高程坡段地形完整性较好,坡度为55°~70°;1 885 m高程线以上主要为变质砂岩、粉砂质板岩,坡度为40°~50°,地形完整性较差。坝顶以上边坡和拱肩槽上游侧边坡的稳定性较差。选取锦屏Ⅰ级水电站左岸拱肩槽开挖边坡作为研究对象,运用式(3) 对各项评价指标实测数据进行归一化处理,各项评价指标的取值范围取各评价等级对应数值范围的并集,得到各项评价指标标准值如表 2所示。
| 表 2 各项评价指标的实测值和标准值 Table 2 Measured values and standard values for each evaluation index |
通过对专家走访调查汇总取权重均值即为主观权重。为保证权重的客观性,借鉴投影寻踪法[23]求解客观权重思想,选择边坡稳定性各项评价指标各等级标准区间中较大的界限值以及实测值构建评价矩阵X,其中前5行为标准序列,最后1行为实测值序列,选取的6组数据均为客观性强的数据,因而避免了专家凭经验赋分,这在很大程度上消除了主观因素的影响,真实地反映了客观指标之间固有的联系。
按照熵权法原理,计算得到各项评价指标的客观权重W2。综合各项评价指标主观权重和客观权重,根据最小信息熵原理,通过式(1) 计算得到指标组合权重W,如表 3所示。对各项评价指标等级标准进行归一化,通过式(4) 对各评价指标等级标准实现云转化,得到对应的云模型参数,运用正向云发生器生成评价指标各等级的隶属云。将各评价指标实测数据标准值代入X-条件云发生器便可求解各项评价指标对应各评价等级的隶属度,根据最大隶属度原则确定二级指标归属等级,见表 4。为更好地理解,以指标X44为例,给出其隶属度计算结果云图,如图 1所示。
| 表 3 各项评价指标权重 Table 3 Weights of each evaluation index |
| 表 4 二级指标的等级综合评价结果 Table 4 Grade comprehensive evaluation for second class index |
|
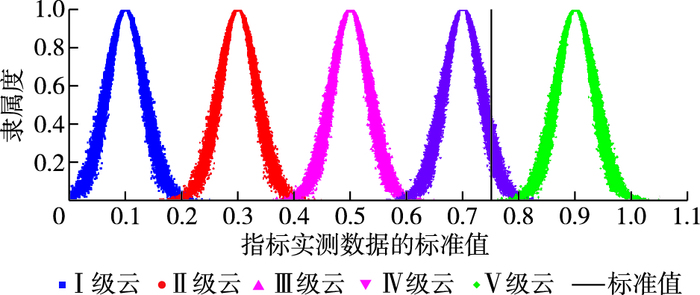
图 1 指标X44的评价结果 Figure 1 Evaluation results for index X44 |
由表 4可知,X44对应各等级的隶属度分别为:R(V)=0.368,R(Ⅳ)=0.616,R(Ⅲ)=0.016,R(Ⅱ)=0,R(Ⅰ)=0,显然R(Ⅳ)> R(V)>R(Ⅲ)>R(Ⅱ)=R(Ⅰ),说明指标X44隶属于Ⅳ级的程度较大,隶属于Ⅴ级和Ⅲ级有一定可能,但相对较小,这与实际意义相符。图 1直观地反映了该计算结果,指标X44明显落在Ⅳ级云上,落在Ⅴ级云和Ⅲ级云较少,几乎不落在Ⅱ级云和Ⅰ级云上。
结合表 3中各项评价指标的组合权重,运用式(8) 计算可得4个一级指标对应各评价等级的隶属度,并确定一级指标归属等级,见表 5。
| 表 5 一级指标的等级综合评价结果 Table 5 Grade comprehensive evaluation for first class index |
结合表 5中一级指标综合隶属度及其权重W=(0.321,0.232,0.221,0.226),运用式(8) 进行矩阵运算便可得到等级综合评价隶属度向量,从而确定边坡稳定性的最终等级L,通过式(6) 和(7) 的计算可以求解隶属度向量的模糊熵E,最终得到高边坡稳定性二维评价结果(L,E)。其具体评价结果详见表 6。
| 表 6 不同方法高边坡稳定性评价结果的比较 Table 6 Comparison between evaluation results of high slope stability obtained from different approaches |
由表 6可知,本文评价方法评价等级隶属度落在R(Ⅳ)上相对明显,约为0.374 1,故该高边坡稳定性等级评定为Ⅳ级。从隶属度的大小来看,当评价指标值随时间发生变化,边坡稳定性等级有可能上升为V级。文中为佐证本文提出方法的有效性,表 6特列出文献[4]评价方法的计算结果来加以说明,从其最终计算结果可判其评价等级同为Ⅳ级,表明该边坡安全稳定性皆有富余,同时亦说明本文评价方法的可行性和科学性,其具体优势有:① 在对边坡稳定性进行等级评价基础上,引入模糊熵,分析了等级综合评价结果的复杂程度,精确地刻画了等级综合评价结果的模糊熵,即0.908。对照等级评价结果与模糊熵的对应关系区间,确定其属于“明显”级别,说明各项评价指标等级归属差别较小,边坡评价结果的复杂程度较低。模糊熵较好地反映了高边坡稳定性评价中各项评价指标等级归类不一致情况下的复杂程度,亦不失本文提出方法的科学性,使边坡稳定性评价由单一等级评价转变为由等级与复杂程度共同构成的二维评价模式。② 可拓评价方法较好地处理了边坡稳定性评价中模糊性问题,但忽略了评价过程中指标的随机性,通过引进模糊云理论,利用两种云发生器将边坡稳定性评价过程中的随机性和模糊性转化为定量的隶属度,综合考虑了评价过程中的随机性和模糊性。③ 改变了仅以单一方法确定各项评价指标权重方式,有效结合了专家调查法和熵权法,熵权法有效利用了各项评价指标实测数据,保证了指标权重的客观性。采用熵组合权重法确定各项评价指标组合权重,融合了各项评价指标的主客观因素。
4 结语针对高边坡稳定性评价中指标赋权及其模糊隶属度等不确定问题,提出了适用于高边坡稳定性的组合赋权模糊云评价方法,同时融合并改进了熵组合权重法和X-条件云模型及模糊熵理论,主要结论如下:
(1) 所提方法在指标赋权及梯层定量评价方面有明显优势,对各层评价指标均可做出量化评价结果。
(2) 熵权法有效利用了各项评价指标实测数据,保证了指标权重的客观性,借助最小信息熵原理的熵组合权重法,能融合评价体系中各项指标的主观因素和客观因素,使各项评价指标权重更符合工程实际。
(3) 利用X-条件云模型,综合考虑边坡稳定性综合评价的随机性和模糊性,以模糊熵作为辅助参评量,可分析等级综合评价结果的复杂程度,实现了高边坡稳定性二维评价模式提升,同时该方法亦可推广应用于其他水工建筑物安全评价。
| [1] |
邢小弟, 张磊, 谈叶飞, 等. 降雨入渗过程中土质边坡稳定性计算[J]. 水利水运工程学报, 2014(3): 98-103. ( XING Xiaodi, ZHANG Lei, TAN Yefei, et al. Calculation method for soil slope stability under the action of precipitation infiltration[J]. Hydro-Science and Engineering, 2014(3): 98-103. (in Chinese)) |
| [2] |
赵建军, 贺宇航, 黄润秋, 等. 基于因子分析法的边坡稳定性评价指标权重[J]. 西南交通大学学报, 2015, 50(2): 325-330. ( ZHAO Jianjun, HE Yuhang, HUANG Runqiu, et al. Weights of slope stability evaluation indexes based on factor analysis method[J]. Journal of Southwest Jiaotong University, 2015, 50(2): 325-330. (in Chinese)) |
| [3] |
苏怀智, 吴中如, 戴会超, 等. 三峡永久船闸高陡边坡整体稳定性的多因素综合评价[J]. 岩石力学与工程学报, 2005, 24(1): 23-32. ( SU Huaizhi, WU Zhongru, DAI Huichao, et al. Multiple-index assessment for global stability of high-steep rock slope of the Three Gorges project permanent shiplock[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(1): 23-32. (in Chinese)) |
| [4] |
谈小龙, 徐卫亚, 梁桂兰. 可拓方法在岩石边坡整体安全评价中的应用[J]. 岩石力学与工程学报, 2009, 28(12): 2503-2509. ( TAN Xiaolong, XU Weiya, LIANG Guilan. Application of extenics method to comprehensive safety evaluation of rock slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(12): 2503-2509. DOI:10.3321/j.issn:1000-6915.2009.12.017 (in Chinese)) |
| [5] |
秦植海, 秦鹏. 高边坡稳定性评价的模糊层次与集对分析耦合模型[J]. 岩土工程学报, 2010, 32(5): 706-711. ( QIN Zhihai, QIN Peng. Evaluation coupling model for high slope stability based on fuzzy analytical hierarchy process-set pair analysis method[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(5): 706-711. (in Chinese)) |
| [6] |
徐飞, 徐卫亚, 刘造保, 等. 基于PSO-PP的边坡稳定性评价[J]. 岩土工程学报, 2011, 33(11): 1708-1713. ( XU Fei, XU Weiya, LIU Zaobao, et al. Slope stability evaluation based on PSO-PP[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(11): 1708-1713. (in Chinese)) |
| [7] |
罗勇. 大冶铁矿露天采场岩质边坡稳定性评价体系与分析方法研究[D]. 武汉: 武汉工程大学, 2012. (LUO Yong. A study of evaluation system and stability analysis of rock slope in the open pit of Daye Iron Mine[D]. Wuhan: Wuhan Institute of Technology, 2012. (in Chinese))
|
| [8] |
何海鹰, 胡甜, 赵健. 基于AHP的岩质高边坡风险评估指标体系[J]. 中南大学学报(自然科学版), 2012, 43(7): 2861-2868. ( HE Haiying, HU Tian, ZHAO Jian. Risk assessment indexes system of high rock slope based on AHP[J]. Journal of Central South University (Science and Technology), 2012, 43(7): 2861-2868. (in Chinese)) |
| [9] |
王新民, 康虔, 秦健春, 等. 层次分析法-可拓学模型在岩质边坡稳定性安全评价中的应用[J]. 中南大学学报(自然科学版), 2013, 44(6): 2455-2462. ( WANG Xinmin, KANG Qian, QIN Jianchun, et al. Application of AHP-extenics model to safety evaluation of rock slope stability[J]. Journal of Central South University (Science and Technology), 2013, 44(6): 2455-2462. (in Chinese)) |
| [10] |
LIU Z, SHAO J, XU W, et al. Comprehensive stability evaluation of rock slope using the cloud model-based approach[J]. Rock Mechanics and Rock Engineering, 2013, 47(6): 2239-2252. |
| [11] |
SU H, LI J, CAO J, et al. Macro-comprehensive evaluation method of high rock slope stability in hydropower projects[J]. Stochastic Environmental Research and Risk Assessment, 2014, 28(2): 2111-2116. |
| [12] |
舒苏荀, 龚文惠. 边坡稳定分析的神经网络改进模糊点估计法[J]. 岩土力学, 2015, 36(7): 349-361. ( SHU Suxun, GONG Wenhui. An improved fuzzy point estimate method for slope stability analysis based on neural network[J]. Rock and Soil Mechanics, 2015, 36(7): 349-361. (in Chinese)) |
| [13] |
马毅, 王希良, 刘振, 等. 基于模糊因素的岩质边坡地震稳定性多模型组合评价[J]. 岩土力学, 2011, 32(增1): 624-629. ( MA Yi, WANG Xiliang, LIU Zhen, et al. Multiple model combination evaluation of seismic stability of rock slope based on fuzzy factors[J]. Chinese Journal of Rock and Soil Mechanics, 2011, 32(Suppl1): 624-629. (in Chinese)) |
| [14] |
陈滔, 邓建辉, 李林芮, 等. 强烈松弛岩质边坡变形特征与稳定性评价[J]. 岩石力学与工程学报, 2015, 34(增1): 2607-2616. ( CHEN Tao, DENG Jianhui, LI Linrui, et al. Deformation characteristics and stability evaluation of a heavily loosened rock slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(Suppl1): 2607-2616. (in Chinese)) |
| [15] |
DAFTARIBESHELIA A, ATAEIB M, SERESHKIB F. Assessment of rock slope stability using the Fuzzy Slope Mass Rating (FSMR) system[J]. Applied Soft Computing, 2011, 11(8): 4465-4473. DOI:10.1016/j.asoc.2011.08.032 |
| [16] |
罗毅, 李昱龙. 基于熵权法和灰色关联分析法的输电网规划方案综合决策[J]. 电网技术, 2013, 37(1): 76-80. ( LUO Yi, LI Yulong. Comprehensive decision-making of transmission network planning based on entropy weight and grey relational analysis[J]. Power System Technology, 2013, 37(1): 76-80. (in Chinese)) |
| [17] |
朱雪龙. 应用信息论基础[M]. 北京: 清华大学出版社, 2001. ( ZHU Xuelong. Fundamentals of applied information theory[M]. Beijing: Tsinghua University Press, 2001. (in Chinese))
|
| [18] |
李健, 汪明武, 徐鹏, 等. 基于云模型的围岩稳定性分类[J]. 岩土工程学报, 2014, 36(1): 83-87. ( LI Jian, WANG Mingwu, XU Peng, et al. Classification of stability of surrounding rock using cloud model[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(1): 83-87. DOI:10.11779/CJGE201401006 (in Chinese)) |
| [19] |
帅青燕, 何亚伯. 基于云模型的坝基岩体质量综合评价[J]. 东南大学学报(自然科学版), 2013, 43(增1): 54-58. ( SHUAI Qingyan, HE Yabo. Comprehensive evaluation on rock quality of dam foundation based on cloud model[J]. Journal of Southeast University(Natural Science Edition), 2013, 43(Suppl1): 54-58. (in Chinese)) |
| [20] |
刘锋, 魏光辉. 基于灰色关联的水利工程方案模糊优选[J]. 水力发电学报, 2012, 31(1): 10-14, 26. ( LIU Feng, WEI Guanghui. Fuzzy optimization of hydraulic project scheme based on improved grey relation analysis[J]. Journal of Hydroelectric Engineering, 2012, 31(1): 10-14, 26. (in Chinese)) |
| [21] |
杨光, 刘敦文, 褚夫蛟, 等. 基于云模型的隧道塌方风险等级评价[J]. 中国安全生产科学技术, 2015, 11(6): 95-101. ( YANG Guang, LIU Dunwen, CHU Fujiao, et al. Evaluation on risk grade of tunnel collapse based on cloud model[J]. Journal of Safety Science and Technology, 2015, 11(6): 95-101. (in Chinese)) |
| [22] |
SUN P, LIU Y, QIU X, et al. Hybrid multiple attribute group decision-making for power system restoration[J]. Expert Systems with Applications, 2015, 42: 6795-6805. DOI:10.1016/j.eswa.2015.05.001 |
| [23] |
周红梅. 基于改进的AHP-PP模型的重力坝安全综合评价方法[J]. 水电能源科学, 2014, 32(2): 59, 90-92. ( ZHOU Hongmei. Comprehensive evaluation of dam safety based on improved AHP-PP mode[J]. Water Resources and Power, 2014, 32(2): 59, 90-92. (in Chinese)) |
 2017
2017 
