2. 河海大学 水利水电学院,江苏 南京 210098
混凝土已被广泛应用于土木、水利工程中,但同时混凝土又是一种多元、多相、非均质准脆性材料,其复杂性和随机性导致了在浇筑、养护和环境变化过程中都可能出现各种缺陷,如微裂纹、不密实等,这些都将影响结构的耐久性和稳定性[1-2]。而空洞是混凝土常见的内部缺陷之一,是浇筑时内含杂物或振捣不完整等原因而形成的内部实体缺失现象。
在国外,Mu和Schultz等采用非线性有限元法对偏心竖向荷载作用下的空心墙进行稳定性分析,探讨了内部空洞深度对于临界轴向荷载的影响[3];Liu和Fok等利用声发射测定压向荷载作用下表面有盒状空洞的复合树脂陶瓷材料的断裂性能[4];Hashimoto等通过观测轴承钢的内部缺陷引起的裂缝扩展过程,指出夹杂物导致的空洞会降低钢的疲劳寿命并提出修复措施[5]。在国内,孙国有将细观空洞扩张与Ⅰ-Ⅱ复合型裂纹相结合,推导相应断裂参量[6];王志杰分析了围岩内出现断裂空洞现象的原因,揭示该现象的可预测性,并用算例进行验证[7];蔺海晓以弹性损伤机理的有限元程序模拟空心砖的抗折能力,探讨空洞率对抗折强度的影响规律[8];Zhao等研究了脆性岩石在单轴压向荷载作用下圆柱形空洞的断裂演化过程[9]。在混凝土断裂方面,徐世烺提出双K模型并进行大量试验[10-12],范向前和胡少伟等开展大量断裂试验并结合声发射特性分析断裂过程[13-15],积极地推进国内混凝土断裂特性研究。
但目前对于有缺陷的混凝土力学行为研究成果较少,尤其是考虑内部空洞缺陷对混凝土断裂性能影响的研究。另外,徐世烺将双K断裂模型应用于丹江口大坝的结构安全性评价[16],但也未能考虑含缺陷混凝土对结构力学行为的影响。鉴于此,本文以含空洞的混凝土为研究对象,采用改进型的楔入劈拉测试装置开展8组试验,研究空洞缺陷尺寸、位置的变化对断裂性能的影响规律。
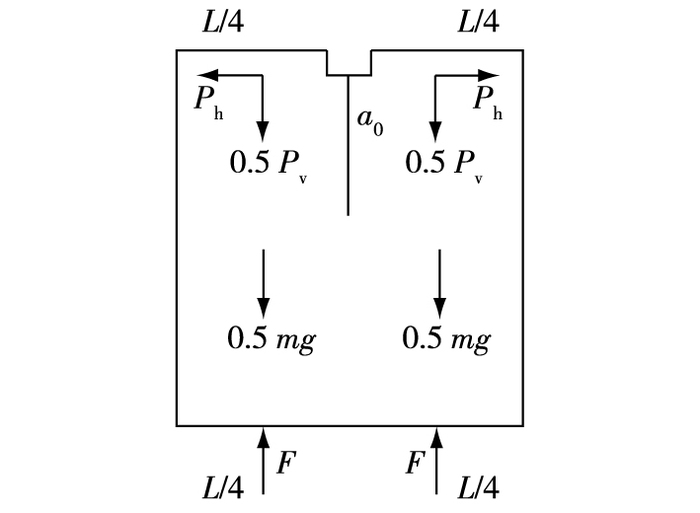
1 断裂参数的确定 1.1 楔入劈拉断裂参数推导徐世烺等[19]进行楔入劈拉试验时,利用支承体、传力装置的荷载处于同一竖向平面内的方式抵消了竖向荷载和部分试件自重,从而获得较为可靠的断裂参数。本次试验中,将采用团队研制的改进型传力装置进行试验[17],该装置对于任何尺寸楔入劈拉试件都能实现荷载加载点位于试件上部四分点处,同时下部支座置于底面四分点处,这样能恰好确保荷载竖向分力、自重、支座反力处于同一竖向平面,使得支座反力能够抵消自重和荷载竖向分力,也消除自重的偏心作用,根据力平衡条件,其受力状况能简化为仅受一对水平拉力作用,如图 1。
|
图 1 试件受力 Figure 1 Force diagram of specimen |
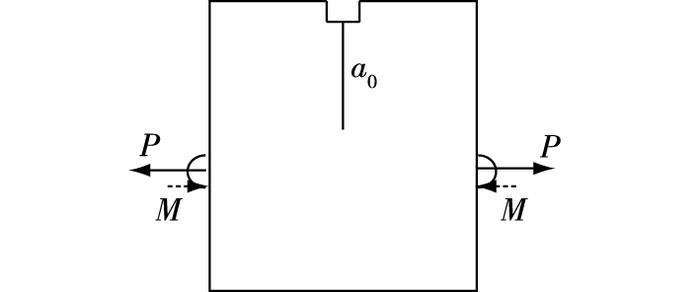
根据图 1和力的叠加原理,受力分解成受拉和受弯两种情况(见图 2)。因此,可将楔入劈拉试件问题视为是单边开口受拉作用和单边开口受弯作用两部分的和。
|
图 2 等效水平拉力 Figure 2 Equivalent horizontal tensile force |
单边开口受拉作用的裂缝长度a和张口位移(crack mouth opening displacement, CMOD)V1存在以下关系[20]:
| $\begin{array}{*{20}{c}} {{V_1} = \frac{{4\sigma a}}{E}f\left( {\frac{a}{h}} \right)}\\ {f\left( {\frac{a}{h}} \right) = \left[ {1.46 + 3.42\left( {1 - \cos \frac{{{\rm{\pi }}a}}{{2h}}} \right)} \right]/{{\left( {\cos \frac{{{\rm{\pi }}a}}{{2h}}} \right)}^2};\sigma = P/\left( {ht} \right)} \end{array}$ | (1) |
单边开口受弯作用裂缝长度a和张口位移V2也有类似关系[20]:
| $\begin{array}{*{20}{c}} {{V_2} = \frac{{24M}}{{E{{\left( {h - {a_0}} \right)}^2}}}g\left( {\frac{a}{h}} \right)}\\ {M = 0.5P\left( {h - {a_0}} \right);g\left( {\frac{a}{h}} \right) = 0.8 - 1.7\left( {\frac{a}{h}} \right) + 2.4{{\left( {\frac{a}{h}} \right)}^2} + 0.66/{{\left( {1 - \frac{a}{h}} \right)}^2}} \end{array}$ | (2) |
式中:E为计算弹性模量;P为水平荷载;h为试件高度;t为试件厚度;a0为预制缝长度;σ为应力;M为弯矩。
楔入劈拉试件张口位移等于式(1) 和(2) 的和,即:
| $V = {V_1} + {V_2} = \frac{{4\sigma a}}{E}f\left( {\frac{a}{h}} \right) + \frac{{24M}}{{E{{\left( {h - {a_0}} \right)}^2}}}g\left( {\frac{a}{h}} \right)$ | (3) |
把起裂荷载Pini、张口位移Vini和初始缝长a0代入式(3),整理后得弹性模量的计算式为:
| $E = \frac{1}{{{V_{{\rm{ini}}}}}}\left[ {\frac{{4{P_{{\rm{ini}}}}{a_0}}}{{ht}}f\left( {\frac{{{a_0}}}{h}} \right) + \frac{{12{P_{{\rm{ini}}}}}}{{h - {a_0}}}g\left( {\frac{{{a_0}}}{h}} \right)} \right]$ | (4) |
再将失稳荷载Pun、失稳张口位移Vun代入式(3) 中,整理后,迭代计算求解出临界有效裂缝长度ac:
| $\begin{array}{l} \frac{{{V_{{\rm{un}}}}}}{{4{P_{{\rm{un}}}}}}E = \frac{{{a_{\rm{c}}}}}{{ht}}\left[ {1.46 + 3.42\left( {1 - \cos \frac{{{\rm{\pi }}{a_{\rm{c}}}}}{{2h}}} \right)} \right]/{\left( {\cos \frac{{{\rm{\pi }}{a_{\rm{c}}}}}{{2h}}} \right)^2} + \\ \frac{3}{{h - {a_0}}}\left[ {0.8 - 1.7\left( {\frac{{{a_{\rm{c}}}}}{h}} \right) + 2.4{{\left( {\frac{{{a_{\rm{c}}}}}{h}} \right)}^2} + \frac{{0.66}}{{{{\left( {1 - {a_{\rm{c}}}/h} \right)}^2}}}} \right] \end{array}$ | (5) |
单边开口受拉作用的韧度计算:
| $\begin{array}{*{20}{c}} {{K_1} = \sigma \sqrt {{\rm{\pi }}a} {f_1}\left( {\frac{a}{h}} \right)}\\ {{f_1}\left( {\frac{a}{h}} \right) = 1.122 - 0.231\left( {\frac{a}{h}} \right) + 10.55{{\left( {\frac{a}{h}} \right)}^2} - 21.71{{\left( {\frac{a}{h}} \right)}^3} + 30.382{{\left( {\frac{a}{h}} \right)}^4}} \end{array}$ | (6) |
单边开口受弯作用的韧度计算:
| $\begin{array}{*{20}{c}} {{K_2} = \frac{{6M}}{{t{{\left( {h - {a_0}} \right)}^2}}}\sqrt {{\rm{\pi }}a} {g_1}\left( {\frac{a}{h}} \right)}\\ {{g_1}\left( {\frac{a}{h}} \right) = 1.122 - 1.4\left( {\frac{a}{h}} \right) + 7.33{{\left( {\frac{a}{h}} \right)}^2} - 13.08{{\left( {\frac{a}{h}} \right)}^3} + 14.0{{\left( {\frac{a}{h}} \right)}^4}} \end{array}$ | (7) |
将这两部分进行叠加,即可得到试件的断裂韧度计算式:
| $K = {K_1} + {K_2} = \frac{P}{{ht}}\sqrt {{\rm{\pi }}a} {f_1}\left( {\frac{a}{h}} \right) + \frac{{3P}}{{t\left( {h - {a_0}} \right)}}\sqrt {{\rm{\pi }}a} {g_1}\left( {\frac{a}{h}} \right)$ | (8) |
在式(8) 中,代入起裂荷载Pini、起裂张口位移Vini和初始裂缝长a0就能够得到起裂韧度;代入失稳荷载Pun、失稳张口位移Vun和临界有效裂缝长度ac就能够得到失稳韧度。
相比规范[18],该计算式仅需要起裂、失稳状态的测量值就能确定断裂韧度,不需要荷载张口位移过程曲线,不需要计算初始线性段的斜率和柔度,能有效降低参数误差累积和过程量对韧度的影响,还能适用于各种尺寸试件的断裂计算。
1.2 等效高度计算对于含空洞缺陷的试件应分别按单边开口受拉作用和单边开口受弯作用考虑空洞缺陷对试件的影响。空洞引起内部实体缺失,导致结构的抗拉、抗弯能力降低。假定试件厚度不变,抗拉、抗弯能力的降幅可通过高度损失量来反映。
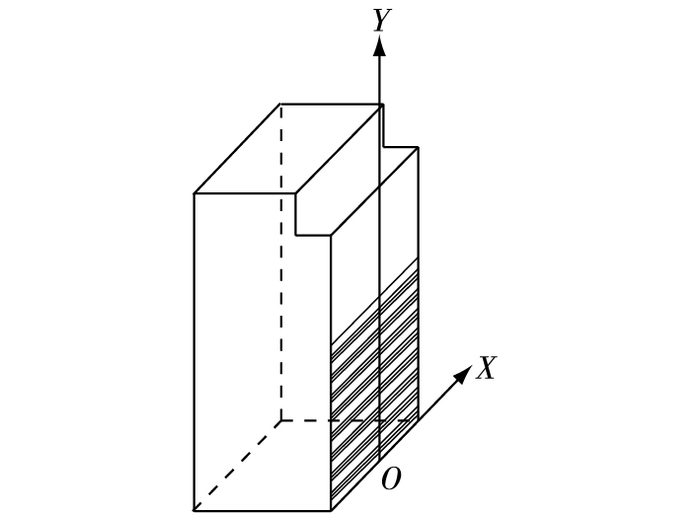
如图 3所示,试件在受拉作用时,空洞使得截面横截面积减小,导致抗拉能力降低,原截面为S0=t×(h-a0)空洞引起了截面πr2损失,将截面损失等效到阴影区域高度的损失,即:
| ${h_{{\rm{s1}}}} = \left( {h - {a_0}} \right)\frac{{t\left( {h - {a_0}} \right) - {\rm{\pi }}{r^2}}}{{t\left( {h - {a_0}} \right)}}$ | (9) |
|
图 3 试件1/2模型 Figure 3 A half model |
而阴影区域等效后高度hs1加上试件上部的(预制缝a0)高度就等于受拉等效后的高度h1:
| ${h_1} = {h_{{\rm{s1}}}} + {a_0}$ | (10) |
如图 3所示,试件在受弯作用时,阴影区域内面积减少,导致该区域的抗弯能力下降,表现为截面抗弯刚度EI降低(E为弹性模量,I为惯性矩,与建立的坐标轴位置有关,抗弯刚度是试件抵抗弯曲变形的能力,是截面的固有属性)。
无空洞时,截面刚度为:
| $EI = Et\int\limits_0^{h - {a_0}} {{y^2}{\rm{d}}y} = E\frac{{t{{\left( {h - {a_0}} \right)}^3}}}{3}$ | (11) |
有空洞时,截面刚度为:
| $EI = E\left( {{I_x} - {I_c}} \right) = E\left[ {\frac{{t{{\left( {h - {a_0}} \right)}^3}}}{3} - \frac{{{\rm{\pi }}{r^4}}}{4} - {\rm{\pi }}{r^2}{{\left( { - c - r + h - {a_0}} \right)}^2}} \right]$ | (12) |
式中:c为预制缝尖端至空洞外层的距离,r为空洞半径。将空洞引起抗弯刚度的减少等效到阴影区域高度的损失,即:
| ${h_{{\rm{s2}}}} = \left( {h - {a_0}} \right)\left[ {1 - \frac{{{\rm{\pi }}{r^4}/4 + {\rm{\pi }}{r^2}{{\left( { - c - r + h - {a_0}} \right)}^2}}}{{t{{\left( {h - {a_0}} \right)}^3}/3}}} \right]$ | (13) |
而阴影区域等效后的高度hs2加上试件上部(预制缝a0)高度就等于受弯作用等效后的高度h2:
| ${h_2} = {h_{{\rm{s2}}}} + {a_0}$ | (14) |
而针对不同形状、位置、尺寸的空洞缺陷,只要能确定其形心坐标和面积就能按上述方式进行等效,实现空洞量化的描述。
1.3 含空洞缺陷的断裂参数表达式已知起裂荷载Pini、起裂张口位移Vini、失稳荷载Pun、失稳张口位移Vun,将等效后的h1,h2代入式(4),(5),(8),整理后得到含空洞缺陷试件的断裂参数表达式:
计算弹性模量:
| $E = \frac{1}{{{V_{{\rm{ini}}}}}}\left[ {\frac{{4{P_{{\rm{ini}}}}{a_0}}}{{{h_1}t}}f\left( {\frac{{{a_0}}}{{{h_1}}}} \right) + \frac{{12{P_{{\rm{ini}}}}}}{{{h_2} - {a_0}}}g\left( {\frac{{{a_0}}}{{{h_2}}}} \right)} \right]$ | (15) |
临界有效裂缝长度:
| $\begin{array}{l} \frac{{{V_{{\rm{un}}}}}}{{4{P_{{\rm{un}}}}}}E = \frac{{{a_{\rm{c}}}}}{{{h_1}t}}\left[ {1.46 + 3.42\left( {1 - \cos \frac{{{\rm{\pi }}{a_{\rm{c}}}}}{{2{h_1}}}} \right)} \right]/{\left( {\cos \frac{{{\rm{\pi }}{a_{\rm{c}}}}}{{2{h_1}}}} \right)^2} + \\ \frac{3}{{{h_2} - {a_0}}}\left[ {0.8 - 1.7\left( {\frac{{{a_{\rm{c}}}}}{{{h_2}}}} \right) + 2.4{{\left( {\frac{{{a_{\rm{c}}}}}{{{h_2}}}} \right)}^2} + \frac{{0.66}}{{{{\left( {1 - {a_{\rm{c}}}/{h_2}} \right)}^2}}}} \right] \end{array}$ | (16) |
断裂韧度:
| $K = \frac{P}{{{h_1}t}}\sqrt {{\rm{\pi }}a} {f_1}\left( {\frac{a}{{{h_1}}}} \right) + \frac{{3P}}{{t\left( {{h_2} - {a_0}} \right)}}\sqrt {{\rm{\pi }}a} {g_1}\left( {\frac{a}{{{h_2}}}} \right)$ | (17) |
| $\begin{array}{*{20}{c}} {{f_1}\left( {a/h} \right) = 1.122 - 0.231\left( {a/{h_1}} \right) + 10.55{{\left( {a/{h_1}} \right)}^2} - 21.71{{\left( {a/{h_1}} \right)}^3} + 30.382{{\left( {a/{h_1}} \right)}^4}}\\ {{g_1}\left( {a/h} \right) = 1.122 - 1.4\left( {a/{h_2}} \right) + 7.33{{\left( {a/{h_2}} \right)}^2} - 13.08{{\left( {a/{h_2}} \right)}^3} + 14.0{{\left( {a/{h_2}} \right)}^4}} \end{array}$ |
试验设计8组楔入劈拉试件(共32个),混凝土强度等级为C25,浇筑时采用标号32.5普通硅酸盐水泥,5~20 mm粒径的碎石,天然中砂,细度模数为2.6,砂率34%,配合比为水泥:砂:石:水=1:1.38:2.79:0.47。试件其他设计参数见表 1。试件浇筑于木模中,按标准养护60 d成型。初始预制缝用厚3 mm、V型30°刀口钢板预埋。空洞模拟体采用空心不锈钢球体,浇筑时表面包裹薄胶带并涂抹黄油,以隔绝混凝土与球体表面接触,再埋入试件。BF120-40AA型号电阻应变片(标距4 cm)贴于缝尖两侧和下方部位,声发射探头交叉布置在试件表面。
| 表 1 试件设计参数 Table 1 Design parameters of specimens |
试验在南京水利科学研究院结构大厅的压力机上进行。试验采用力控方式,慢速均匀加载至0.58 kN,持荷30 s,以确保仪器安装无误和连接良好,之后正式试验,并以恒定加载速度施加荷载直至试件破坏,整个加载过程历时约33 min。
试件破坏形态如图 4所示,从预制缝下方一分为二,与常规楔入劈拉断裂破坏形式一致。其中,1#组是无空洞的常规楔入劈拉试件,2#~7#组试件试验时在起裂后裂纹稳定扩展,经过空洞断面之后才进入失稳状态;8#组是试件失稳扩展后才经过空洞断面。试验后发现空洞表面光滑且轻微触碰球体随即自然脱落,表明包裹薄胶带和涂抹黄油能够使得空心不锈钢球体与混凝土接触不良,确保球体模拟空洞缺陷。试验中,使用声发射和应变片法共同确定起裂、失稳状态,并准确获取对应状态的张口位移和荷载测量值。

|
图 4 试件破坏形态和空洞 Figure 4 Specimen failure and cavity |
将试件分别按式(9)~(14) 计算出各自的等效高度h1,h2,如表 2所示,r为空洞半径,c为预制缝尖端距离空洞表层的垂直距离,hs1,hs2为受拉作用和受弯作用两种状态下图 3阴影中的等效高度。
| 表 2 等效高度计算结果 Table 2 Calculated results of equivalent height |
确定起裂、失稳状态后,获得起裂荷载Pini和张口位移Vini,失稳荷载Pun和张口位移Vun,代入式(15),(16) 和(17),计算得到表 3断裂参数。
| 表 3 断裂参数计算结果 Table 3 Calculated results of fracture parameters |
在试验中,含空洞缺陷试件与常规试件的断裂形式基本相似,都是预制缝下部的区域在荷载作用下,萌生微裂纹且逐步发展并形成宏观裂缝,最终导致试件破坏,如图 4。而且都经历起裂、裂纹稳定扩展、失稳阶段,荷载-张口位移曲线在加载初期张口位移随荷载线性增长,起裂后张口位移增幅速度加大,此后不再满足线性关系,裂纹随荷载增加而稳定扩展,直至发生失稳破坏。但各组试件的起裂、失稳荷载和韧度都随空洞尺寸、位置的变化而存在差异。
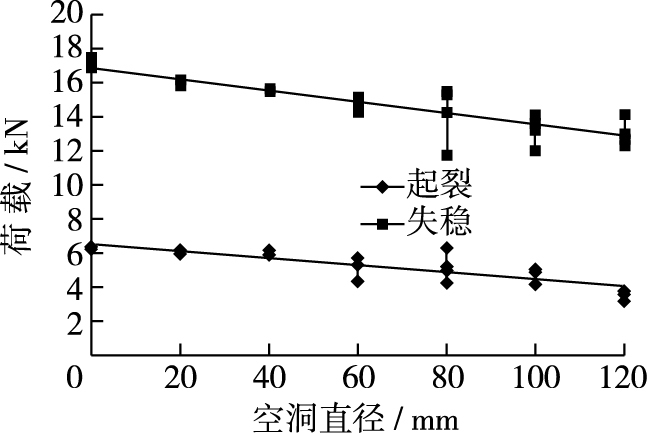
从表 3和图 5可见,起裂荷载、失稳荷载随空洞尺寸增大逐渐减小。常规试件起裂荷载为6.24 kN,随空洞尺寸增加(直径0,20,40,60,80,100,120 mm)而减小至3.52 kN,降幅43.59%。空洞尺寸对起裂荷载影响较为显著,这是由于空洞引起了内部实体缺失,使试件抗弯、抗拉能力下降,导致试件在承受较小荷载和弯矩时就提前起裂。另外,在裂纹稳定扩展时,内部实体缺失减小了裂纹克服黏聚力需消耗的能量,使裂缝更快地发展,导致试件提前失稳,失稳荷载由17.117 kN随空洞尺寸增加而降低至13.052 kN,降幅23.75%。
|
图 5 荷载随空洞直径变化 Figure 5 Curves of load and radius of cavity |
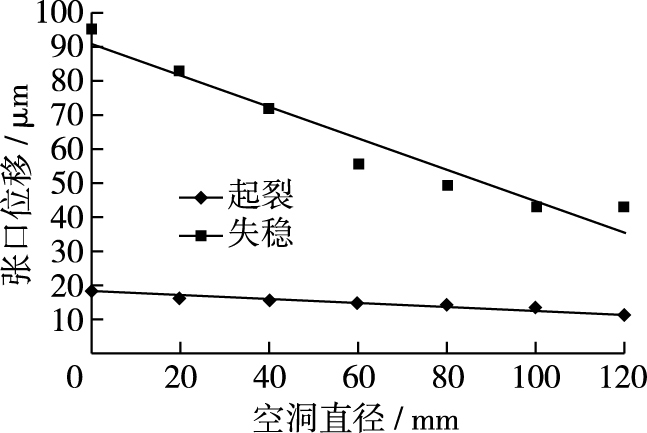
另外,由于张口位移与荷载存在对应关系,所以起裂、失稳的张口位移也同样呈现相同变化规律,即张口位移随着空洞尺寸增加而降低,如图 6所示。起裂张口位移从18.305 μm降至11.01 μm,降幅39.85%,失稳张口位移从94.77 μm降至43.14 μm,降幅54.5%。
|
图 6 张口位移随空洞直径变化 Figure 6 Curves of CMOD and radius of cavity |
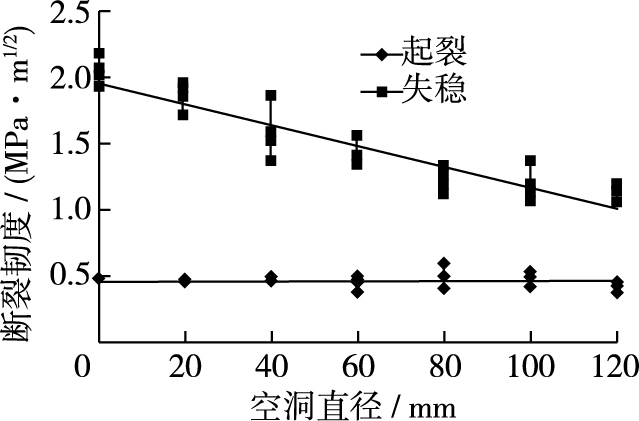
由图 7可见,由于空洞尺寸不同,双K断裂韧度存在差异。具体表现为:起裂韧度较小,且基本保持稳定;失稳韧度却随着空洞尺寸增大而逐渐下降。起裂韧度0.449 MPa·m1/2至0.489 MPa·m1/2,其微小差异可视为混凝土材料自身离散性造成,不影响整体规律。该数值稳定性也再次证实了起裂韧度是材料的固有属性,不随结构形式改变而发生变化。对比表 3,失稳韧度从2.05 MPa·m1/2降至1.103 MPa·m1/2,降幅46.20%,表明空洞尺寸对失稳韧度影响较为明显。失稳韧度的降低是由于试件在承受荷载作用时提前起裂,而空洞又减少了裂纹扩展克服黏聚力需消耗的部分能量,加速裂缝发展导致试件提前失稳。这正是空洞缺陷的隐患之一,空洞的存在使结构本身更加脆弱,抗外界荷载能力降低,并提前引起裂纹萌生,且加速内部裂纹扩展,从而导致结构更加容易发生破坏。
|
图 7 断裂韧度随空洞直径变化曲线 Figure 7 Curves of fracture toughness and diameter of cavity |
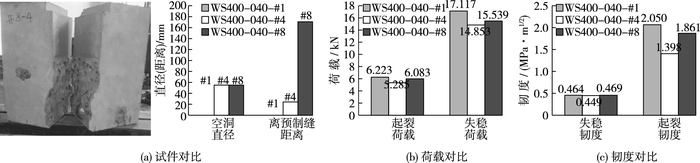
对比图 8,WS400-040-1#是常规试件(无空洞),而WS400-040-4#, WS400-040-8#的空洞尺寸60 mm,离预制缝的距离分别为25和180 mm,从表 3和图 8可见,由于空洞位置变化,试件的荷载和韧度都有较大差异。4#组裂缝失稳前经过空洞,而8#组空洞远离断裂区,直至失稳后裂缝才经过空洞。对比计算结果,4#,8#起裂荷载分别为5.285和6.083 kN,差值0.789 kN;失稳荷载14.854和15.539 kN,差值0.685 kN;起裂韧度0.449和0.469 MPa·m1/2,基本相等;失稳韧度1.398和1.861 MPa·m1/2,差值0.463 MPa·m1/2。4#比1#的起裂、失稳荷载和失稳韧度分别降低0.938 kN,2.264 kN和0.652 MPa·m1/2,而8#的起裂、失稳荷载和失稳韧度却降低0.14 kN,1.578 kN和0.189 MPa·m1/2。4#的荷载、韧度的降幅都高于8#,是因为8#的空洞远离裂缝稳定扩展区域,仅引起试件提前起裂,在起裂后空洞却不影响裂缝扩展。这说明了空洞位置能影响试件的断裂特性,但其影响程度取决于与裂缝稳定扩展区域的距离,如果空洞处于该区域,其表现如2#至7#组,显著地降低起裂、失稳荷载、张口位移和失稳韧度等参数;如果空洞远离该区域,则对断裂参数影响较不明显。
|
图 8 试件、荷载和韧度对比 Figure 8 Comparison of specimen groups, load and toughness |
基于改进型的楔入劈拉测试装置,将空洞缺陷等效为纵向截面高度的损失量,并推导出了含空洞缺陷混凝土楔入劈拉断裂参数的计算式,该式仅需起裂、失稳状态的测量值即可确定混凝土断裂参数,无需荷载张口位移过程曲线,也不需要计算初始V-F和柔度。通过试验分析得出以下结论:
(1) 混凝土的起裂荷载、失稳荷载都会随着内部空洞尺寸的增大(0~120 mm)而逐步下降,其降幅分别为43.59%和23.75%;起裂、失稳张口位移也同样随着空洞尺寸的增大而缓慢降低,降幅分别为39.85%和54.50%。
(2) 起裂韧度基本不随空洞尺寸变化而明显变化,是材料的固有属性,其值为0.449~0.489 MPa·m1/2,但失稳韧度却会随着空洞尺寸的增大而下降,降幅为46.20%。
(3) 空洞位置对断裂特性的影响与其距离裂纹扩展区域有关,如裂纹扩展时经过空洞区,则会明显降低混凝土的起裂、失稳荷载、张口位移和失稳韧度等,如果裂缝远离空洞区则对断裂性能影响相对较小。
| [1] |
朱伯芳, 许平. 加强混凝土坝面保护尽快结束"无坝不裂"的历史[J]. 水力发电, 2004, 30(3): 25-28. ( ZHU Bofang, XU Ping. Strengthen superficial insulation of concrete dams to terminate the history of "on dam without cracks"[J]. Water Power, 2004, 30(3): 25-28. (in Chinese)) |
| [2] |
徐世烺. 混凝土断裂力学[M]. 北京: 科学出版社, 2011: 2-6. ( XU Shilang. Concrete fracture mechanics[M]. Beijing: Science Press, 2011: 2-6. (in Chinese))
|
| [3] |
LV M, SCHULTZ A E, STOLARSKI H K. Influence of cavity dimension on the stability of eccentrically loaded slender unreinforced masonry hollow walls[J]. Construction and Building Materials, 2011, 25(12): 4444-4453. DOI:10.1016/j.conbuildmat.2011.04.001 |
| [4] |
LIU X Z, FOK A S L, LI H Y. Influence of restorative material and proximalcavity design on the fracture resistance of MOD inlay restoration[J]. Dental Materials, 2014, 30: 327-333. DOI:10.1016/j.dental.2013.12.006 |
| [5] |
HASHIMOTO K, FUJIMATSU T, TSUNEKAGE N, et al. Effect of inclusion/matrix interface cavities on internal-fracture-type rolling contact fatigue life[J]. Materials and Design, 2011, 32(10): 4980-4985. DOI:10.1016/j.matdes.2011.06.056 |
| [6] |
孙国有, 薛继良, 兰清生, 等. 空洞扩张与Ⅰ-Ⅱ复合型裂纹的断裂参量[J]. 浙江大学学报(自然科学版), 1994, 28(1): 1-7. ( SUN Guoyou, XUE Jiliang, LAN Qingsheng, et al. Void growth and fracture criteria of cracks of mixed Ⅰ and Ⅱ modes[J]. Journal of Zhejiang University(Natural Science), 1994, 28(1): 1-7. (in Chinese)) |
| [7] |
王志杰. 围岩断裂空洞现象的启示[C]//第十一次全国岩石力学与工程学术大会论文集, 2010: 184-188. (WANG Zhijie. Inspiration of surrounding rock crack cavity phenomenon[C]// 11st National Academic Conference of Rock Mechanics and Engineering, 2010: 184-188. (in Chinese))
|
| [8] |
蔺海晓, 付磊. 混凝土空心砖抗折性能数值研究[J]. 建筑材料学报, 2012, 15(6): 778-781. ( LIN Haixiao, FU Lei. Numerical study on bending behavior of concrete perforated brick[J]. Journal of Building Materials, 2012, 15(6): 778-781. (in Chinese)) |
| [9] |
ZHAO X D, ZHANG H X, ZHU W C. Fracture evolution around pre-existing cylindrical cavities in brittle rocks under uniaxial compression[J]. Transactions of Nonferrous Metals Society of China, 2014, 24(3): 806-815. DOI:10.1016/S1003-6326(14)63129-0 |
| [10] |
XU S L, REINHARDT H W. A simplified method for determining double-K fracture parameters for three-point bending tests[J]. International Journal of Fracture, 2000, 104: 181-209. DOI:10.1023/A:1007676716549 |
| [11] |
XU S L, REINHARDT H W. Crack extension resistance and fracture properties of quasi-brittle softening materials like concrete based on the complete process of fracture[J]. International Journal of Fracture, 1998, 92: 71. DOI:10.1023/A:1007553012684 |
| [12] |
ZHAO Y H, XU S L, LI Z J. An analytical and computational study on energy dissipation along fracture process zone in concrete[J]. Computers & Concrete, 2004, 1(1): 47-60. |
| [13] |
FAN X Q, HU S W, ZHU H T. SFRC subjected to domestic sewage and sustained load[J]. Journal Wuhan Univ Technol-Mat Sci Edit, 2012, 27(4): 797-804. DOI:10.1007/s11595-012-0551-y |
| [14] |
HU Shaowei, LU Jun, FAN Xiangqian. The fracture of concrete based on acoustic emission[J]. Advanced Materials Research, 2011, 137(7): 261-265. |
| [15] |
FAN Xiangqian, HU Shaowei. Influence of crack initiation length on fracture behaviors of reinforced concrete[J]. Applied Clay Science, 2013, 79: 25-29. DOI:10.1016/j.clay.2013.02.026 |
| [16] |
吴瑶, 徐世烺, 吴建营, 等. 双K断裂准则在丹江口大坝安全性评定中的应用[J]. 水利学报, 2015, 46(3): 366-372. ( WU Yao, XU Shilang, WU Jianyin, et al. Application of double-K fracture criterion in evaluating Danjiangkou dam safety[J]. Journal of Hydraulic Engineering, 2015, 46(3): 366-372. (in Chinese)) |
| [17] |
胡少伟, 徐爱卿. 非标准混凝土楔入劈拉试件高宽比影响分析[J]. 硅酸盐学报, 2015, 43(10): 1492-1499. ( HU Shaowei, XU Aiqing. Effect analysis on fracture morphology of non-standard concrete wedge splitting tests by different height to width ratio[J]. Journal of the Chinese Ceramic Society, 2015, 43(10): 1492-1499. (in Chinese)) |
| [18] |
DL/T 5332—2005水工混凝土断裂试验规程[S]. (DL/T 5332—2005 Norm for fracture test of hydraulic concrete[S]. (in Chinese))
|
| [19] |
赵艳华, 韩飞, 陈晋. 楔入劈拉断裂试验支承形式对混凝土断裂韧度的影响[J]. 水利水电科技进展, 2009, 29(4): 10-13. ( ZHAO Yanhua, HAN Fei, CHEN Jin. The effect of support on concrete fracture toughness in wedge-splitting test[J]. Advances in Science and Technology of Water Resources, 2009, 29(4): 10-13. DOI:10.3880/j.issn.1006-7647.2009.04.003 (in Chinese)) |
| [20] |
TADA H, PARIS P C, IRWIN G R. The stress analysis of cracks handbook[M]. New York: ASME Press, 2000.
|
2. College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing 210098, China
 2017
2017 

